Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes

Show all

12661 to 12720 of 14420

  1. <
  2. 1
  3. ...
  4. 208
  5. 209
  6. 210
  7. 211
  8. 212
  9. 213
  10. 214
  11. 215
  12. ...
  13. 241
  14. >

    • We had discussed here at some length the formalization of formally etale morphisms in a differential cohesive (infinity,1)-topos. But there is an immediate slight reformulation which I never made explicit before, but which is interesting to make explicit:

      namely I used to characterize formal étaleness in terms of the canonical morphism ϕ:i !→i *\phi : i_! \to i_* between the components of the geometric morphism i:H↪H thi : \mathbf{H} \hookrightarrow \mathbf{H}_{th} that defines the differential cohesion – because that formulation made close contact to the way Kontsevich and Rosenberg formulate formal étaleness.

      But there is a more suggestive/transparent but equivalent (in fact more general, since it works in all of H th\mathbf{H}_{th} not just in H\mathbf{H}) formulation in terms of the Π inf\mathbf{\Pi}_{inf}-modality, the “fundamental infinitesimal path ∞\infty-groupoid” operator:

      a morphism f:X→Yf : X \to Y in H th\mathbf{H}_{th} is formally étale precisely if the canonical diagram

      X → Π inf(X) ↓ f ↓ Π inf(f) Y → Π inf(Y) \array{ X &\to & \mathbf{\Pi}_{inf}(X) \\ \downarrow^{\mathrlap{f}} && \downarrow^{\mathrlap{\mathbf{\Pi}_{inf}(f)}} \\ Y &\to& \mathbf{\Pi}_{inf}(Y) }

      is an ∞\infty-pullback.

      (It’s immediate that this is equivalent to the previous definition, using that i !i_! is fully faithful, by definition.)

      This is nice, because it makes the relation to general abstract Galois theory manifest: if we just replace in the above the infinitesimal modality Π inf\mathbf{\Pi}_{inf} with the finite path ∞\infty-groupoid modality Π\mathbf{\Pi}, then the above pullback characterizes the “Π\mathbf{\Pi}-closed morphisms” which precisely constitute the total space projections of locally constant ∞\infty-stacks over YY. Here we now characterize general ∞\infty-stacks over YY.

      And for instance in direct analogy with the corresponding proof for the Π\mathbf{\Pi}-modality, one finds for the Π inf\mathbf{\Pi}_{inf}-modality that, for instance, we have an orthogonal factorization system

      (Π inf−equivalences,formallyetalemorphisms). (\mathbf{\Pi}_{inf}-equivalences\;,\; formally\;etale\;morphisms) \,.

      I’ll spell out more on this at Differential cohesion – Structures a little later (that’s why this here is under “latest changes”), for the moment more details are in section 3.7.3 of differential cohomology in a cohesive topos (schreiber).

    • added to disk a brief pointer to Joyal’s combinatorial disks. Needs to be expanded, probably entry should be split and disambiguated. But no time right now.

    • I have started something in an entry

      layers of foundations

      which has grown out of the the desires expressed in the thread The Wiki history of the universe.

      This is tentative. I should have maybe created this instead on my personal web. I hope we can discuss this a bit. If it leads nowhere and/or if the feeling is that it is awkward for one reason or other, I promise to remove it again. But let’s give this a chance. I feel this is finally beginning to converge to something.

    • started adding list of references to the page Bill Lawvere

      not that I made it very far -- just three items so far :-)

      I was really looking for an online copy of "Categorical dynamics" as referenced at synthetic differential geometry and generalized smooth algebra, but haven't found it yet. I was thinking that the "Toposes of laws of motion" that I do reference must be something close. But I don't know.

    • New, mainly disambiguation, entry affine algebra. Note that affine algebra for most algebraists is not the same as affine Lie algebra. I have corrected a wrong link in Wess-Zumino model which links to affine algebra instead to affine Lie algebra; let us be careful when linking in future. Affine algebras are coordinate rings of affine varieties. I have split affine variety from algebraic variety which also got a redirect algebraic manifold (= smooth algebraic variety). New entry Igor Shafarevich.

    • I created Alex Heller at Jim’s suggestion. It is very stubby and could have a lot more added.

    • New entry (!) tangent Lie algebra. Significant changes at invariant differential form with redirect invariant vector field reflecting the vector fields and other tensor cases. Many more related entries listed at and the whole entry reworked extensively at Lie theory. Some changes at Lie’s three theorems and local Lie group. New stubs Chevalley group and Sigurdur Helgason.

      By the way, when writing tangent Lie algebra, I had the problem with finding the correct font for the standard symbol of Lie algebra of vector fields on a manifold. Usually one has varchi symbol which looks like Greek chi but with dash through middle. The varchi symbol is not recognized and I put mathcal X which is slanted and script, just alike, but without dash through middle.

      By the way, on a real Lie group GG of dimension nn, if one expresses the right invariant vector field in terms of left invariant vector fields then at each point there is a ℝ\mathbb{R}-linear operator which sends any frame of left invariant vector fields to the corresponding frame in right invariant vector fields; this gives a GL n(ℝ)GL_n(\mathbb{R})-valued real analytic function on GG (or, in local coordinates, on a neighborhood of the unit element). In other words, if I take a frame in a Lie algebra and interpret it in two ways, as a frame of left invariant vector fields and a frame in right invariant vector fields, then I can take a matrix of real analytic functions on a Lie group and multiply the frame of left invariant vector fields with this matrix to get the correspoding frame of right invariant vector fields. I use in my current research some computations involving this matrix function. Does anybody know of any reference in literature which does any computations involving this matrix valued function on GG ?

    • A stub Massey product and a longer Toda bracket (still plenty gaps of reference, many many unlinked words). No promises w.r.t. spellings.

      I now see I’ve missed the convention for capitalization. Will fix that now… done.

      Cheers

    • I am hereby moving the following old Discussion box from interval object to here

      Urs Schreiber: this is really old discussion by now. We might want to start putting dates on discussions. In principle it can be seen from the entry history, but readers glancing at this here hardly will. Maybe discussions like this here are better had at the forum after all.

      We had originally started discussing the notion of interval objects at homotopy but then moved it to this entry here. The above entry grew out of the following discussion we had, together with discussion at Trimble n-category.

      Urs: Let me chat a bit about what I am looking for here. It seems very useful to have a good notion of what it means in a context like a closed category of fibrant objects to say that path objects are compatibly corepresented.

      By this should be meant: there exists an object II such that

      • for BB any other object, [I,B][I,B] is a path object;

      • and such that II has some structure and property which makes it “nice”.

      In something I am thinking about the main point of II being nice is that it can model compositon: it must be possible to put two intervals end-to-end and get an interval of twice the length. In some private notes here I suggest that:

      a “category with interval object” should be

      I think there are a bunch of obvious examples: all familiar models of higher groupoids (Kan complexes, ω\omega-groupoids etc.) with the interval object being the obvious cellular interval {a→≃c}\{a \stackrel{\simeq}{\to} c\}.

      I also describe one class of applications which I think this is needed/useful for: recall how Kenneth Brown in section 4 of his article on category of fibrant objects (see theorems recalled there and reference given there) describes fiber bundles in the abstract homotopy theory of a pointed category of fibrant objects. This is pretty restrictive. In order to describe things like ∞\infty-vector bundles in an context of enriched homotopy theory one must drop this assumption of the ambient category being pointed. The structure of it being a category with an interval object is just the necessary extra structure to still allow to talk of (principal and associated) fiber bundles in abstract homotopy theory. It seems.

      Comments are very welcome.

      Todd: The original “Trimblean” definition for weak nn-categories (I called them “flabby” nn-categories) crucially used the fact that in a nice category TopTop, we have a highly nontrivial TopTop-operad where the components have the form hom Top(I,I ∨n)\hom_{Top}(I, I^{\vee n}), where X∨YX \vee Y here denotes the cospan composite of two bipointed spaces (each seen as a cospan from the one-point space to itself), and the hom here is the internal hom between cospans.

      My comment is that the only thing that stops one from generalizing this to general (monoidal closed) model categories is that “usually” II doesn’t seem to be “nice” in your sense here, and so one doesn’t get an interesting (nontrivial) operad when my machine is applied to the interval object. But I’m generally on the lookout for this sort of thing, and would be very interested in hearing from others if they have interesting examples of this.

      to be continued in the next comment

    • I noticed that the text at loop space didn’t point to smooth loop space and didn’t make clear that such a variant might even exist. So I have now expanded the Idea-section there a little to give a better picture.

    • I have received a question on the old entry directed object, so I am looking at that now. First of all I’ll clean it up a bit and move old discussion from there to here:

      [begin forwarded discussion]

      +–{.query}

      Eric: I don’t fully “grok” this constructive definition, but I like its flavor. Is it possible to formalize the procedure in a simple catchy phrase? In other words, when you begin with a “category CC with interval object II”, but whose objects are otherwise undirected (like Top), you construct the “supercategory d ICd_I C” with directed CC-objected (even though no objects in CC are directed). I used the term “directed internalization”, but is there a better term?

      I just think this concept is important and should have some really slick arrow theoretic description and I’m not having any luck coming up with one myself.

      =–

      [ continued in next post ]

    • finally expanded the long-existing table of contents complex geometry - contents and included it as a floating TOC in the relevant entries.

      Do we have more entries that need to go here and which I have forgotten?

    • did I say that I created Theta space?

      This is a really nice model. Rezk claims to have shown to get the homotopy hypothesis right for all (n,r)-categories and for both n and r ranging to 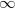\infty . If that holds water, it's quite impressive. It seems the only thing missing then is the 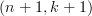(n+1,k+1)- Theta-space of all 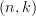(n,k)-Theta spaces. Does anyone know if there is a proposal for that?

      It's also interesting how the result is a mix of globular and simplicial shapes. So in what respect does that build on/improve over Joyal's original proposal?

    • A query about the new entry on copncurrency theory: Does ‘simultaneously’ make sense if there is no global clock?

      If not, then the situation gets a lot more like some models for spacetime and the idea of slices through some evolving state space might be a good model.

    • Someone, apparently in Berlin, has created a page called www.mfo.de/document/1145/OWR_2011_52.pdf, with just that text (and ’My First Slide’) in the body. The URL points to a report on a logic workshop at Oberwolfach around this time last year. It’s not spam, but what should we do with it?

    • Someone signing themselves as ‘Joker? at November 3, 2012 08:05:13 from 93.129.88.58’ deleted two lines from sheaf and topos theory. There seemed no reason for this, so I have rolled back to the previous version.

    • The recent changes to the various modal logic pages have changed the emphasis from the ’many agent’ versions S4(m)S4(m).etc. to a type theoretic one. That would be okay but in so doing they have become a bit garbled so they refer to K(m) but then just describe KK itself. I am wondering what is planned for these. I originally wrote them with the aim of increasing the nPOV side of the Computer Science entries and to have some brief introduction to modal logs, what should they become?

    • October 24, 2012 09:26:08 by Anonymous Coward (99.133.144.164) has added a comment questioning the validity of a sentence at reflective subcategory.

    • wanted to be able to say sum and have a pointer to somewhere.

    • I made starts on lexicographic order and on compactification. Lexicographic order was defined only for products of well-ordered families of linear orders (probably the most common type of application).

      I’m not very happy with the opening of compactification.

    • I edited the old entry projection a little.

      There is no real systematics in common use of “projection” as opposed to “projector”, but I think the following makes good sense:

      1. a projection is a canonical map out of a product;

      2. a projector is an idempotent in a suitably abelian category

      and then the relation is: A projector is a projection followed by a subobject inclusion.

      That’s how I have now put it in the entry.

    • New entry enumerative geometry. New stubs Schubert calculus, intersection theory.

      By the way (Andrew); the title of this nForum post is not seen but truncated. This happens because of some other stuff is placed into the corner in the same line. It says unimportant info “Bottom of Page” preceded by long space between the truncated title and this info ad. I think it is more important that the titles be spelled entirely.

    • created a table of contents idempotents - contents and included it as a floating TOC into the relevant entries

    • While writing at k-morphism, I noticed there is no article on globular operad (aka Batanin operad), so I wrote one. Experts please look over, and improve if desired.

    • While writing the new Idea-section now at Segal condition I felt the need to have a table of contents

      So I started one and added it to the relevant entries as a floating TOC.

    • I think we need a floating table of contents categories of categories - contents to connect our entries on related topics. I have started one.

      But this needs to be further expanded. also haven’t included it into the relevant entries yet, no time right now.

    • I have written out in some detail the proof at Grothendieck spectral sequence.

      But I still need to go through it and proof-read and polish. Handle with care for the moment. Maybe the whole thing needs to be rearranged, for readability.

    • I (only) now realize that I pretty much missed the story of familial regularity and exactness. But also it was easy to miss, with the entries that are unified by this not pointing back to it.

      To rectify this I have created now a floating TOC and am including it into all the relevant entries:

      Please check out that TOC and edit/modify as need be.

    • I've done a tiny bit of work to add a more intuitive introduction to the concepts of model category and Quillen equivalence, and I plan to do some more. If anyone wants to help, that would be great. For example, it would be nice to give some general intuition for fibrations, cofibrations and weak equivalences and why they matter.

    • slightly restructured, added table of contents and then added remarks to cobordism hypothesis (in the section "remarks") using material from blog discussion over at SecretBloggingSeminar.

12661 to 12720 of 14420

  1. <
  2. 1
  3. ...
  4. 208
  5. 209
  6. 210
  7. 211
  8. 212
  9. 213
  10. 214
  11. 215
  12. ...
  13. 241
  14. >
Top of Page