Processing math: 100%
Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration finite foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes

Show all

13021 to 13080 of 15597

  1. <
  2. 1
  3. ...
  4. 214
  5. 215
  6. 216
  7. 217
  8. 218
  9. 219
  10. 220
  11. 221
  12. ...
  13. 260
  14. >

    • added a paragraph about passing from first-order logic to modal type theory to the entry on analytic philosophy.

    • I’ve made comments at Fivebrane, fivebrane 6-group, Fivebrane structure and differential fivebrane structure regarding the fact String(n) is not 6-connected for n≤6 (though trivially so for n=2).

      There will be a bunch of interesting invariants for manifolds of dimensions 3-6. This includes, for instance, on 6-dimensional spin manifolds a non-torsion class corresponding to the obstruction to lifting the tangent bundle to the 6-connected group covering String(6) (here π5(String(6))=ℤ). This is the only non-torsion example, but should be given by a U(1)-4-gerbe, I think, which will have a 6-form curvature. Since H6 won’t be vanishing for oriented manifolds, one has some checking to do. For instance, the frame bundle of S6 lifted to a String(6)-bundle (I plan to write a paper on this 2-bundle) will not lift to a Fivebrane(6)-bundle, because it won’t even lift to a ˜String(6)-bundle (i.e. the 6-connected cover of String(6)), since the transition function S5→BString(6) is the generator. Thus the 6-form curvature of this 4-gerbe should be the volume form on the 6-sphere.

      Another point that occurs to me is that there are two copies of ℤ to kill off in String(8) to get Fivebrane(8), so one gets a U(1)×U(1) higher gerbe. I suspect this larger π7 is why there are so many more exotic spheres in dimension 15 than in neighbouring dimensions (16256 vs 2 in d=14 and 16); it’s certainly the case for exotic spheres in dimension 7 that π3(SO(4))=ℤ×ℤ helps.

    • Here we are going to explain the application of Topology.

    • have highlighted a bit more the fact here that the atoms in a subtopos lattice are the 2-valued Boolean ones. Thanks to Thomas Holder for alerting me.

      And have added this as an example/proposition to atom and to Boolean topos, too.

    • I threw in some references to the early topos approach to set theory in ETCS. On this occasion I couldn’ t resist the temptation to rearrange somewhat the lay-out of the entry: actually I thought it better not to throw HOTT immediately at the reader and gave Palmgren’s ideas a proper subsection. I’ve also deflated a bit the foundational claims of ETCS sticking more to what appears to me to be Lawvere’s original intentions.

    • This comment is invalid XML; displaying source. <p>I created <a href="https://ncatlab.org/nlab/show/synthetic+differential+geometry+applied+to+algebraic+geometry">synthetic differential geometry applied to algebraic geometry</a> which is supposed to host a question that I am going to post on <a href="http://go2.wordpress.com/?id=725X1342&site=sbseminar.wordpress.com&url=http%3A%2F%2Fmathoverflow.net%2F">math Overflow</a> following the discussion we have of that <a href="http://sbseminar.wordpress.com/2009/10/14/math-overflow/#comment-6875">here at SBS</a>.</p> <p>In that context I also wrote a section at <a href="https://ncatlab.org/nlab/show/algebraic+geometry">algebraic geometry</a> intended to describe the general-nonsense perspective. But that didn't quite find the agreement with Zoran and while we are having some discussion about this in private, he has restructured that entry now.</p>
    • I've asked John Barrett recently and he agrees that the Yetter model and the Crane-Yetter model are two different things. I've written about that in a new article: http://ncatlab.org/nlab/show/Crane-Yetter+model

    • brief entry on Turaev-Viro model, an entry long overdue. But for the moment it just records some references.

      Bruce Bartlett has a comment on what is currently the last of these references and he will post it below in a moment…

    • am creating

      2d TQFT – table

      listing the statements of the classification results, for the various cases. As far as I am aware of them.

    • Created a stub at Milnor K-theory, which is now just an MO answer of Cisinski. To be expanded at some later point when I study this in more detail.

    • I corrected the page overconvergent global analytic geometry about the global unitary group: it is not a group (in the archimedean setting) but a strict analytic $\infty$-groupoid.

      One may thus define $BU(n)$ but the naive space $U(n)$ is not a group.

      In any case, one can still work with $BU(n)$ as if it were a classifying stack, i guess...

      It would be interesting to see if some of the ideas of geometric Langlands still make sense in this setting. Any comments on this?

      And on the possibility of doing higher Chern-Simons using this strange $BU(n)$, Urs?
    • I added this topic because it seems to be the right setting for motivic homotopy theory of overconvergent global analytic spaces (if one wants to have a relation with global Hodge theory in the sense of another entry of nlab).

      Cheers,

      Fred

    • Couldn’t find an existing “latest changes” thread for the quasifibration page (http://ncatlab.org/nlab/show/quasifibration), but just wanted to remark that I put another reference in there, to a nice expository paper by Peter May.

      -Jon

    • I have added pointer to Mike’s discussion of spectral sequences here at “homotopy spectral sequence” and in related entries.

      But now looking at this I am unsure what the claim is: has this been formalized in HoTT?

      (Clearly a question for Mike! :-)

    • expanded the entry cofinal functor: formal definition, list of equivalent characterizations and textbook reference.

    • Hi guys and girls,

      I have set up a new subject on the nlab, related to the previously opened subject of global Hodge theory:

      http://ncatlab.org/nlab/show/Arithmetic+cryptography

      Contributions are welcome (in particular to fill-in the blanc subjects on this page, if you like).

      Fred
    • Hi guys,

      I plan to improve drastically the content of the nlab on Hodge theory, p-adic, classical and global.

      With this perspective in mind, i have made some new topics, and improved the section on global analytic geometry, by adding in particular a new reference of mine that contains a notion of strict global analytic spaces and some perspectives for its use to study various problems of arithmetic geometry.

      The new topics, that should be the place to discuss these subjects if you are interested, are: generalized Lambda-structures and global Hodge theory. I also plan to make a page on special values of L-functions, and another on the spectral interpretation of zeroes and poles of L-functions.

      I don't connect often to the nforum, so i may not discuss a lot about the present message, but the nlab pages will be updated. Contact me by email at frederic.paugam@imj-prg.fr if you would like to discuss these things.

      All the best,

      Frédéric

    • How would you define the usual jargon “fragment” in logic?

      There ought to be a simple formal definition, I suppose, such as “Given a language L and a theory T in that language, then a fragment of T is… “

    • added to periodic ring spectrum and to periodic cohomology theory a brief paragraph on looping/delooping periodicity on the ∞-modules, with a pointer to this MO discussion

    • Discussion with Mike reminded me that we were lacking an entry reflective subuniverse.

      I started a template and cross-linked, but now I am out of battery and time before filling in any content. Will do that tomorrow.

    • This is to flag up two entries that so-far just have titles. They are IulianUdrea and perfectly normal space. These may need watching. The second may be ok, and be a page somone has just started and intends to continue, but the name on the second also occurs as a name on a Mo page with no questions and no answers and may be someone seeing how many wikis etc they can put stuff on! Sorry for being a nasty suspicious b*****, but it looks a bit strange to me.

      (N.B., the two entries do not seem to be related.)

    • at diffeomorphism I started listing theorems and references on statements about when the existence of a homeomorphism implies the existence of a diffeomorphism.

      I dug out ancient references for the statement that in d≠4 everything homeomorphic to an open d-ball is also diffeomorphic to it. What would be a more modern, more canonical, more textbook-like reference for this?

      And I’d also like to cite a reference for what is maybe obvious, that if that something in d=4 is an open subset of ℝ4 equipped with the induced smooth structure of the standard smooth structure, then the statement is also true in that dimension.

      In fact, I am looking for nice/explicit/useful diffeomorphisms from the open n-ball onto the open n-simplex. I can of course fiddle around and cook up something, but I haven’t found anything that would count as nice. But probably some engineer out there working with finite elements or something does have a convenient choice.

    • there is this new master thesis:

      • Cesare Gallozzi, Constructive Set Theory from a Weak Tarski Universe, MSc thesis (2014)

      which discusses aspects of weak Tarskian homotopy type universes following the indications that Mike Shulman has been making, for instance at universe (homotopytypetheory). I just got permission to share this and I have now included pointers to the thesis to that entry, to type of types, etc.

    • At some point I had made up the extra axiom/terminology saying that an object 𝔸1 in a cohesive ∞-topos “exhibits the cohesion” if the shape modality is equivalent to 𝔸1-localization. Now I was talking about that assumption with Mike and noticed that this didn’t have a reflection on the nLab yet.

      So now I have added, for the record, the definition here at “cohesive oo-topos” and cross-linked with the existing discussion at “continuum”.

    • added recent AlgTop mailing list contribution on fibrant replacement of cubical sets to cubical set

    • Urs has created page Stanisław Woronowicz on Sep 10. However there is an old page for the same person, with publication version S. L. Woronowicz in nLab, with extensive reference list which was redirecting the full name Stanisław Lech Woronowicz as well as Stanisław L. Woronowicz.

    • I added to (infinity,n)-category of cobordisms a description in plain English (or what I make of that...) of Lurie's definition of Bord_{(\infty,n)}.

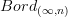      The definition is very simple and elegant, but it is not being exposed really in Lurie's writeup, and the whole definition 2.2.9, which is central to the article, is itself rather hidden somewhere, so I I am making the experience that people staring at the document tend not to see the simple point here. As a reaction to that, I thought I'd write this out now.
    • I added the definition of funcoid in nLab wiki.

      I also call the theory of funcoids "Algebraic General Topology" because it somewhere replaces epsilon-delta notation with more algebraic formulas.

      Feel free to copy more materials about funcoids, reloids, and their generalizations from my site to nLab.

      The theory of funcoids is very productive in creating new open problems and research trends. I welcome to work with me. Read the manuscripts at my site.

    • I’ve written a stub on Cole’s theory of spectrum which for the time being consists largely of references and links. Further curation or correction would be appreciated!

    • added to (infinity,n)-category of spans a pointer to the discussion of (∞,2)-categories of spans in section 10 of

    • David Mumford has a treasure trove of free material at his website, so I added a link to his page.

    • Flattered though I was at being promoted to an n-category cafe author, I had to change 'Roberts' to 'Corfield' at Online resources in the description of our favourite stomping ground. Someone's fingers got the better of them, I didn't look who ^_^

      -David Roberts

    • I have added several historically important references at space-time.

    • I did a bit of editing (of Definition and Examples) at child’s drawing (once known as children’s drawing), to emphasize that a child’s drawing/dessin d’enfant is not simply a hypermap, but (typically) a hypermap seen as the representation of a Belyi function. I was guided by the presentation in Lando & Zvonkin 2004 (this paper by Zvonkin is also helpful), but apologies if I introduced any mistakes since I’m just learning this stuff.

    • Few references collected as a start of entry spectrum of a graph redirecting also Ihara zeta function, prompted by today’s remarkable paper by Huang and Yau and thereby revived memory of a colloqium talk by Bass in which I enjoyed at University of Wisconsin in late 1990s.

    • added to group completion a paragraph with minimum pointers to the traditional construction ΩB(−) as group completion of topological monoids. Added a corresponding brief paragraph to K-theory of a permutative category (where this had been missing).

      What is still missing (on the nLab and maybe generally in the literature) is a really clear statement that this is indeed a model for the ∞-categorical group completion operation which is invoked at K-theory of a symmetric monoidal (infinity,1)-category.

      One place where such a derived functor statement is made is Dwyer-Kan 80, remark 9.7 (thanks to Charles Rezk’s MO comment here). I have added pointers to that to the relevant entries, but this ought to be sorted out in more detail.

13021 to 13080 of 15597

  1. <
  2. 1
  3. ...
  4. 214
  5. 215
  6. 216
  7. 217
  8. 218
  9. 219
  10. 220
  11. 221
  12. ...
  13. 260
  14. >
Top of Page