nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topicAxioms of ZFC
- Category Latest Changes
- Started by TobyBartels
- Comments 1
- Last comment by TobyBartels
- Last Active Jan 16th 2011
Every axiom listed at ZFC now has its own article, except for axiom of separation. These are:
- axiom of extensionality (already existed);
- axiom of the null set (now redirects to empty set, where additional material has just been added);
- axiom of pairing (created recently);
- axiom of union (created recently);
- axiom of separation (needs to be written);
- axiom of replacement (already existed);
- axiom of power sets (now redirects to power set, where a few remarks have just been added);
- axiom of infinity (already existed);
- axiom of choice (already existed);
- axiom of foundation (already existed).
- Discussion Type
- discussion topic[[range]]
- Category Latest Changes
- Started by TobyBartels
- Comments 3
- Last comment by TobyBartels
- Last Active Jan 16th 2011
We don’t use the term “range” much here, and I explained why.
- Discussion Type
- discussion topicEuclidean topology
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by TobyBartels
- Last Active Jan 15th 2011
have created Euclidean topology, for completeness
- Discussion Type
- discussion topicfiltered (infinity,1)-category
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by zskoda
- Last Active Jan 14th 2011
added to filtered (infinity,1)-category the statement that these are precisely those shapes of diagrams such that -colimits over them commute with finite -limits.
- Discussion Type
- discussion topicalgebrad
- Category Latest Changes
- Started by zskoda
- Comments 11
- Last comment by zskoda
- Last Active Jan 14th 2011
algebrad and additions at Nikolai Durov. The movie starts slow and boring but gets very interesting after a while when the topic develops.
- Discussion Type
- discussion topiccohesive infinity-toposes - contents
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 13th 2011
I have created a table of contents cohesive infinity-toposes - contents and have added it as a “floating TOC” to some relevant entries
- Discussion Type
- discussion topicFreedom vs fascism
- Category Latest Changes
- Started by TobyBartels
- Comments 27
- Last comment by David_Corfield
- Last Active Jan 13th 2011
Added a note about cofree functors to free functor.
- Discussion Type
- discussion topicposite
- Category Latest Changes
- Started by Urs
- Comments 18
- Last comment by TobyBartels
- Last Active Jan 12th 2011
I have edited posite
In particular I tried to work the query box into the text. Mike and David R. please check if you agree with the result.
- Discussion Type
- discussion topichomotopy dimension
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Jan 12th 2011
have created an entry homotopy dimension
- Discussion Type
- discussion topicthread
- Category Latest Changes
- Started by zskoda
- Comments 4
- Last comment by TobyBartels
- Last Active Jan 12th 2011
New entry thread needed at newly expanded pro-object. Adequate changes at filtered limit.
While threads are elements in the cofiltered limit of sets or spaces, germs are classes of equivalence which appear in the treatment of filtered colimits. However the entry germ is taking germs just in the special case of colimits forming stalks of an etale space. In my practice the notion of germ could be used more generally for directed colimits or even filtered colimits in groups, sets, and alike. Is it only me using the terminology in this extended sense ? I would like to know the opinions.
- Discussion Type
- discussion topiccohomological dimension
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 12th 2011
have started cohomological dimension
- Discussion Type
- discussion topicoo-cohesive site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 11th 2011
added to infinity-cohesive site statement and proof that if all objects of the -cohesive site have points, then the cohesive -topos over it satisfies the axiomm pieces have points .
(Easy proof using the previous results and Dugger’s cofibrant replacement theorem for ).
- Discussion Type
- discussion topicover-(oo,1)-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 9th 2011
added to over-(infinity,1)-category the statement that the hom-spaces are computes by homotopy fibers of hom-spaces in the underlying -category in direct analogy to the 1-categorical case
- Discussion Type
- discussion topiclocal (oo,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 9th 2011
added at local (infinity,1)-topos
statement and proof that over the -connectivity condition is redundant;
statement and proof that for any -topos over and any small-projective object, the slice is local.
- Discussion Type
- discussion topic(2,1)-site
- Category Latest Changes
- Started by Urs
- Comments 5
- Last comment by TobyBartels
- Last Active Jan 8th 2011
because I needed the link I have created a stub (2,1)-site. I define it there as an (infinity,1)-site whose underlying category is a (2,1)-category. Don’t have the leisure right now to check that this is also a 2-site whose underlying 2-category is a -category, as hopefully it is
- Discussion Type
- discussion topicQuestions by Jim
- Category Latest Changes
- Started by DavidRoberts
- Comments 3
- Last comment by Urs
- Last Active Jan 7th 2011
Lots of questions by Jim Stasheff at descent for L-infinity algebras. But they are not marked clearly, so have a look at the changes.
- Discussion Type
- discussion topicinfinity-connected site
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Jan 6th 2011
have created infinity-connected site
- moved over from infinity-cohesive site the proof that the -topos over a locally and globally -connected site is locally and globally -connected; (and had occasion to polish and streamline it a bit more)
- Discussion Type
- discussion topicstrongly infinity-connected site
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Jan 6th 2011
created strongly infinity-connected site with the analogous definition, analogous proposition and analogous proof as at strongly connected site.
Only difference is that I define it as a cosifted -connected site instead of as a cosifted locally -connected site, because I am currently not quite sure about the definition of the latter because my model-category theoretic proofs rely on the existence of a terminal object, without that my standard Quillen adjunction model for the terminal -geometric morphism fails and I’d need to think harder.
But all these entries of higher connected and local sites currently have the issue that they give sufficient conditions and don’t prove necessary conditions, so I think it’s okay, but we should keep in mind that there might be refinements of these definitions.
- Discussion Type
- discussion topicconnected site
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Jan 6th 2011
created connected site and declared it to be a locally connected site with a terminal object.
That’s sufficient for its sheaf topos to be connected, I don’t now if it is necessary: If we find a weaker sufficient condition we should refine the entry.
- Discussion Type
- discussion topicinfinity-local site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 6th 2011
created infinity-local site (by separating the old material at infinity-cohesive site into its local and its connected bits, the connected bits are now split off at ∞-connected site).
- Discussion Type
- discussion topictotally infinity-connected site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 6th 2011
created totally infinity-connected site with definition, theorem and proof analogous to totally connected site.
- Discussion Type
- discussion topicsifted (oo,1)-category
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Jan 6th 2011
created sifted (infinity,1)-category
- Discussion Type
- discussion topicstrongly connected site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 5th 2011
created strongly connected site with the evident definition and proposition
- Discussion Type
- discussion topicstrongly/totally oo-connected (oo,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 5th 2011
I am trying to polish some entries in the topic cluster of higher connected toposes. In the course of this I felt like creating
mostly for cosmetic reasons at the moment. Not non-trivial content there yes.
- Discussion Type
- discussion topicSkolem
- Category Latest Changes
- Started by zskoda
- Comments 6
- Last comment by zskoda
- Last Active Jan 4th 2011
I plan to write few foundations/set theory stubs including Skolem paradox. It will wait for a bit as the Lab seems to be down at the moment.
The entry forcing has phrase downward Löwenheim-Skolem theorem. What does it mean downward in this phrase ? Is it a modifier at all ?
- Discussion Type
- discussion topicfppf-site
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by zskoda
- Last Active Jan 4th 2011
have created fppf-site
- Discussion Type
- discussion topiclocal site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 4th 2011
created local site
- Discussion Type
- discussion topicconnected topos
- Category Latest Changes
- Started by Mike Shulman
- Comments 2
- Last comment by Urs
- Last Active Jan 3rd 2011
I added a number of facts and proofs to connected topos, and shortened the example since it is a special case of the general fact about connected locally connected sites.
- Discussion Type
- discussion topicn-localic (oo,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Jan 3rd 2011
I rewrote the Idea-section at n-localic (infinity,1)-topos (trying to make it more to the point) and added propositions in the Properties- and the Examples-section.
- Discussion Type
- discussion topicfpqc-site
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by zskoda
- Last Active Jan 3rd 2011
have created fpqc-site
- Discussion Type
- discussion topic(oo,1)-Yoneda lemma
- Category Latest Changes
- Started by Urs
- Comments 13
- Last comment by Urs
- Last Active Jan 2nd 2011
added the full statement to (infinity,1)-Yoneda lemma
It's an easy consequence of the sSet-enriched Yoneda lemma, using the theorem that oo-presheaves are presented by fibrant-cofibrant sSet enriched presheaves.
Notice that this appears without stating the name "Yoneda lemma" as Lemma 5.5.2.1 in HTT. (Beware, though, that there are typos in there. There is a general mix-up of ops already in the statement of the lemma and the first
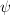 in the proof is a
in the proof is a 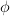 . )
. )
- Discussion Type
- discussion topicstructured (infinity,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Jan 2nd 2011
I rewrote the Idea-section of structured (infinity,1)-topos.
i tried to make it clearer and shorter. And I highlighter more the aspect that this is a way to equip little -toposes with geometric structure.
- Discussion Type
- discussion topichomotopy groups of a Lie groupoid
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Jan 2nd 2011
created homotopy groups of a Lie groupoid
The definition is the one following from the general abstract -topos theoretic notion applied in ooLieGrpd, but I wanted a separate entry for this in order to record the references for that special case
- Discussion Type
- discussion topicapplied mathematics
- Category Latest Changes
- Started by zskoda
- Comments 5
- Last comment by TobyBartels
- Last Active Dec 30th 2010
- Discussion Type
- discussion topiccohesive topos and cohesive site
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Dec 30th 2010
I expanded at cohesive site the example “Families of sets”.
I also started expanding the Examples-section at cohesive topos, but it remains stubby for the moment. I have to run now.
- Discussion Type
- discussion topicprojective stack
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by zskoda
- Last Active Dec 29th 2010
created projective stack
- Discussion Type
- discussion topicsubobject in an (infinity,1)-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 29th 2010
- Discussion Type
- discussion topicIntroduction to [[logic]]
- Category Latest Changes
- Started by TobyBartels
- Comments 5
- Last comment by Tim_Porter
- Last Active Dec 24th 2010
I wrote an introduction to logic. It’s pretty brief, but at least it defines the meanings (one a mass noun, one a count noun) of the word.
- Discussion Type
- discussion topicschematic homotopy type
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 23rd 2010
have started schematic homotopy type
- Discussion Type
- discussion topiccanonical structure sheaves on objects in a big topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 23rd 2010
I have added to the Examples at structured (infinity,1)-topos a section Canonical structure sheaves on objects in a big topos.
For the moment this only contains the observation that for the big topos on a geometry , for every object its little topos is canonically equipped with a -structure sheaf.
This is evident from the discussion at etale geometric morphism, but it nevertheless seems to be noteworthy.
I have added also an inducation on how this canonical structure sheaf is indeed that of -valued functions on . But more details on this would be desireable. But I have to interrupt now.
- Discussion Type
- discussion topicquestion at semigroup
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by TobyBartels
- Last Active Dec 23rd 2010
somebody signing as “Anonymous Coward” dropped a query box with a question at semigroup.
- Discussion Type
- discussion topicorientation
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 21st 2010
tried to bring the entry orientation into a bit of shape
- Discussion Type
- discussion topicshape of an (oo,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Dec 21st 2010
created shape of an (infinity,1)-topos
- Discussion Type
- discussion topiclittle etale topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 17th 2010
created little etale topos
- Discussion Type
- discussion topicquasicoherent (infinity,1)-sheaf
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by zskoda
- Last Active Dec 15th 2010
I worked a bit on quasicoherent (infinity,1)-sheaf:
I polished the account of the model-category theory presentation by Toen-Vezzosi a little
Then I added the slick general abstract definition in terms of the tangent (oo,1)-category that we once discussed, but which nobody had yet filled into this entry
- Discussion Type
- discussion topicinternal ∞-groupoid versus internal groupoid
- Category Latest Changes
- Started by Mike Shulman
- Comments 6
- Last comment by Mike Shulman
- Last Active Dec 14th 2010
The page internal ∞-groupoid claimed that the case of “internal ∞-groupoids in an (∞,1)-category” was discussed in detail at groupoid object in an (∞,1)-category. That doesn’t seem right to me—I think the groupoid objects on the latter page are really only internal 1-groupoids, not internal ∞-groupoids. They’re “∞” in that their composition is associative and unital only up to higher homotopies, but those are homotopies in the ambient (∞,1)-category; they themselves contain no “higher cells” as additional data. In particular, if the ambient (∞,1)-category is a 1-category, then an internal groupoid in the sense of groupoid object in an (∞,1)-category is just an ordinary internal groupoid, no ∞-ness about it. Does that seem right?
- Discussion Type
- discussion topicirreducible polynomial
- Category Latest Changes
- Started by Urs
- Comments 5
- Last comment by zskoda
- Last Active Dec 14th 2010
stub for irreducible polynomial
- Discussion Type
- discussion topicPIE-limits
- Category Latest Changes
- Started by Mike Shulman
- Comments 2
- Last comment by Mike Shulman
- Last Active Dec 14th 2010
- Discussion Type
- discussion topicfully dualizable object
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 13th 2010
created fully dualizable object with Idea and Reference, but too lazy to write out the definition at the moment.
- Discussion Type
- discussion topichomotopy - contents
- Category Latest Changes
- Started by Urs
- Comments 7
- Last comment by Tim_Porter
- Last Active Dec 13th 2010
I added a bunch of entries to homotopy - contents – mostly all the variants of homotopy groups – and inserted the floating TOC to all pages listed there
- Discussion Type
- discussion topicBaues
- Category Latest Changes
- Started by Tim_Porter
- Comments 1
- Last comment by Tim_Porter
- Last Active Dec 12th 2010
I have started listing the contents / chapters on some of Hans Baues books and papers (that I have at hand and that are relevant to the Lab). So far I have done Algebraic Homotopy and Combinatorial Homotopy and 4-Dimensional Complexes, but so far have not tried to give section titles nor to link with other entries.
(Edit: I have now added Homotopy Types, which is his article in the Handbook of Alg. Top. I copied the format from another similar entry but find it a bit heavy, suggestions please. I do intend to list sections and subsections and add more links later.)
- Discussion Type
- discussion topiccell complex
- Category Latest Changes
- Started by Urs
- Comments 10
- Last comment by Tim_Porter
- Last Active Dec 10th 2010
Mr. or Mrs. Anonymous Coward created cell complex but didn’t have much to say. Maybe somebody feels like helping the Coward.
(Is such activity failed spam or failed contribution?)
- Discussion Type
- discussion topicmodel structure on sSet-presheaves
- Category Latest Changes
- Started by Urs
- Comments 6
- Last comment by Harry Gindi
- Last Active Dec 10th 2010
edited model structure on sSet-presheaves a little
- Discussion Type
- discussion topicdifferential forms on presheaves/on simplicial sets
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Dec 10th 2010
split off differential forms on presheaves from rational homotopy theory. Expanded and edited differential forms on simplices.
- Discussion Type
- discussion topicetale (infinity,1)-site
- Category Latest Changes
- Started by Urs
- Comments 23
- Last comment by zskoda
- Last Active Dec 9th 2010
created etale (infinity,1)-site
- Discussion Type
- discussion topicdg-operad
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 9th 2010
stub for dg-operad
- Discussion Type
- discussion topicmodel structure on dg-operads
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 9th 2010
stub for model structure on dg-operads
- Discussion Type
- discussion topicblob n-category
- Category Latest Changes
- Started by Urs
- Comments 8
- Last comment by Urs
- Last Active Dec 9th 2010
I extracted the definition of “n-category with all duals” from Scott Morrison and Kevin Walker’s “Blob homology” at blob n-category.
This is to some extent a take on defining hyperstructures.
- Discussion Type
- discussion topicsSet-site
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Dec 9th 2010
edited sSet-site a little
- Discussion Type
- discussion topicbicategory of relations
- Category Latest Changes
- Started by Todd_Trimble
- Comments 22
- Last comment by FinnLawler
- Last Active Dec 9th 2010
Someone left a query at bicategory of relations, and I put down a partial response (proving the separability condition). I plan to add a little more later, but I confess that I don’t see how to derive the other dual Frobenius condition from the one given. (Hard to believe the dual one wasn’t given by Carboni and Walters.)
Carboni and Walters call a “bicategory of relations” a discrete cartesian bicategory (because the local posets of maps are discrete). They are equivalent to unitary pretabular allegories.