nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
- Discussion Type
- discussion topicdifferential topology of mapping spaces
- Category Latest Changes
- Started by Andrew Stacey
- Comments 28
- Last comment by Urs
- Last Active May 13th 2010
I’ve started porting my notes “differential topology of loop spaces” over to the nlab, starting at differential topology of mapping spaces. As part of the transfer, I intend to map out the theory for general mapping spaces, not just loop spaces (that’ll give me a bit more motivation to do the transfer since just cut-and-paste is boring!). I’ve just copied over the contents and the introduction so far and haven’t edited them as yet. In particular, although I’ve wikilinked all the original section names, these will get changed as they currently focus on loop spaces.
The introduction to the original document ended as follows (not copied over to the new version):
This document began life as notes from talks given at NTNU and at Sheffield so I would like to thank the topologists at those institutions, and in particular Nils Baas, for letting me talk about my favourite mathematical subject. I would also like to thank Ralph Cohen and the “loop group” at Stanford.
This is by no means a finished document, as an example it is somewhat sparse on references. Any comments, suggestions, and constructive criticism will be welcomed.
The second paragraph is sort-of stating the obvious as it holds to some extent for any nLab page! And I would love to be able to add some more names to the list in the first paragraph. Again, I hope it goes without saying but I’ll say it anyway: although I anticipate being the main contributor to these pages, it is not my project! I would love it if people read it, add comments, add other stuff, write (constructive) graffiti, link it to other stuff.
- Discussion Type
- discussion topicmapping space
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active May 13th 2010
Currently mapping space redirects to internal hom.
I have now at least added a link to Andrew’s recent manifold structure of mapping spaces to the list of examples there, but it wouldn’t hurt if someone wrote a bit more about mapping spaces in topology etc.
- Discussion Type
- discussion topiccover
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active May 12th 2010
The entry cover was in a pitiful state. I tried to brush it up a bit. But I am afraid I am still not doing it justice. But also I don’t quite have the leisure for a good exposition right now. What I really want is to create an entry good cover in a moment…
- Discussion Type
- discussion topicSullivan construction
- Category Latest Changes
- Started by Urs
- Comments 5
- Last comment by Urs
- Last Active May 12th 2010
stub for Sullivan construction (I got annoyed that the entry didn’t exist, but also don’t feel like doing it justice right now)
- Discussion Type
- discussion topick-tuply monoidal n-category
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active May 11th 2010
Because I want to point to it in a reply to the current discussion on the Category Theory Mailing list, I tried to brush up the entry k-tuply monoidal n-category a bit.
In particular I
- Discussion Type
- discussion topicAT category
- Category Latest Changes
- Started by Todd_Trimble
- Comments 7
- Last comment by Todd_Trimble
- Last Active May 11th 2010
I had started an article on AT category (which I originally mis-titled as “AT categories” – thank you Toby for fixing this!), but getting a little stuck here and there. I’m using the exchange between Freyd and Pratt on the categories mailing list (what else is there?) as my reference, but as is so often the case, Freyd’s discussion is a little too snappy and terse for me to follow it down to all the nitty-gritty details.
There’s a minor point I’m having trouble verifying: that coproducts are disjoint (as a consequence of the AT axioms that Freyd had enunciated thus far where he made that claim, in his main post), particularly that the coprojections are monic. Presumably this isn’t too hard and I’m just being dense. A slightly less than minor point: I’m having trouble verifying Ab-enrichment of the category of type A objects. I believe Freyd as abelian-categories-guru implicitly – I don’t doubt him. Can anyone help?
- Discussion Type
- discussion topicinvariant polynomial
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active May 10th 2010
created invariant polynomial
- Discussion Type
- discussion topicNoncommutative geometry and stochastic calculus
- Category Latest Changes
- Started by Eric
- Comments 6
- Last comment by Todd_Trimble
- Last Active May 8th 2010
Todd is helping me understand opposite categories beginning with here.
This discussion helped prompt some improvement of the page opposite category. When I look at that page now, I see the statement:
The idea of noncommutative geometry is essentially to define a category of spaces as the opposite category of a category of algebras.
This reminded me of a remark I made in the “Forward” to a paper I wrote back in 2002, so I’ve now itexified that “Foreward” here:
Noncommutative Geometry and Stochastic Calculus
By the way, this also suggests that the category is the category of spaces opposite to the category of finite Boolean algebras in the sense of space and quantity.
- Discussion Type
- discussion topicspinors in Yang-Mills theory
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Tim_van_Beek
- Last Active May 7th 2010
I noticed that recently Konrad Waldorf created a very nice article
I went through it and added definition/theorem/proof-environments and lots of hyperlinks. Some of them are unsaturated. Maybe somebody feels inspired to create corresponding entries.
- Discussion Type
- discussion topicessential geometric morphism
- Category Latest Changes
- Started by Urs
- Comments 10
- Last comment by Urs
- Last Active May 7th 2010
started essential geometric morphism
- Discussion Type
- discussion topictrig & pi
- Category Latest Changes
- Started by Michael Hardy
- Comments 7
- Last comment by Urs
- Last Active May 6th 2010
- trigonometric identities and the irrationality of pi
I created this new page. I'm new here and I have no idea whether this sort of thing belongs in a place like this.
-- naively.....
- Discussion Type
- discussion topicobject
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active May 6th 2010
expanded object
- Discussion Type
- discussion topicnew and revised pages on logic stuff
- Category Latest Changes
- Started by Todd_Trimble
- Comments 3
- Last comment by Mike Shulman
- Last Active May 6th 2010
- Recently have been adding to or creating various pages like essentially algebraic theory, Lawvere theory, Horn theory, signature, theory, and there may be others.
- Discussion Type
- discussion topicEilenberg-Zilber theorem
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active May 5th 2010
added the cosimplicial version of the statement to Eilenberg-Zilber theorem and included a reference that gives a proof
- Discussion Type
- discussion topicClosed functors
- Category Latest Changes
- Started by TobyBartels
- Comments 18
- Last comment by Urs
- Last Active May 4th 2010
Eric wanted to know about closed functors, so we started a page. Probably somebody has written about these before, so references would be nice, if anybody knows them. (Google gives some hits that look promising, but I can’t read them now.)
- Discussion Type
- discussion topicHousekeeping at Frolicher spaces
- Category Latest Changes
- Started by Andrew Stacey
- Comments 1
- Last comment by Andrew Stacey
- Last Active May 4th 2010
I’ve done a bit of housekeeping at Froelicher space. I’ve split the page into pieces, putting each major section into its own section.
(This will necessitate a little reference chasing at manifolds of mapping spaces, and I need to put in some redirects)
I’ve put in a definition of curvaceous compactness at topological notions of Frölicher spaces. It works, but I’m not sure if it’s the right one yet.
- Discussion Type
- discussion topicexponential law
- Category Latest Changes
- Started by zskoda
- Comments 8
- Last comment by Mike Shulman
- Last Active May 4th 2010
It seems to me that despite so lenghty discussions and entry related to the mapping space-hm adjunction, only the ideal situations are treated (convenient categories of spaces). For this reason, I have created a new entry exponential law for spaces containing the conditions usually used in the category of ALL topological spaces, as well as few remarks about the pointed spaces.
- Discussion Type
- discussion topiccircle bundle
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active May 3rd 2010
created stub for circle bundle
- Discussion Type
- discussion topiccircle group
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Andrew Stacey
- Last Active May 3rd 2010
proudly presenting the circle group ;-)
- Discussion Type
- discussion topicsmooth (oo,1)-algebra
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active May 2nd 2010
split off smooth (infinity,1)-algebra from derived smooth manifold and (infinity,1)-algebraic theory
- Discussion Type
- discussion topiccategorification and groupoidification
- Category Latest Changes
- Started by bwebster
- Comments 10
- Last comment by bwebster
- Last Active May 2nd 2010
Taking the advice that if I write something on the internet, it should be stuck on the n-Lab, I've converted my recent comments in the n-category cafe and some old blog posts into a new page on the relationship between categorification and groupoidification: categorification via groupoid schemes
- Discussion Type
- discussion topicmanifolds of mapping spaces
- Category Latest Changes
- Started by Andrew Stacey
- Comments 21
- Last comment by Eric
- Last Active May 1st 2010
Split off the mapping spaces stuff from local addition into manifolds of mapping spaces. Still plenty to do and things to check (particularly on the linear stuff, and particularly figuring out what “compact” means). Haven’t actually deleted the relevant bit from local addition yet. Also, haven’t put a table of contents at manifolds of mapping spaces since I’ve learnt that the best way to get Urs to read something is to not put a toc in.
- Discussion Type
- discussion topicsub-quasi-category
- Category Latest Changes
- Started by Urs
- Comments 8
- Last comment by Urs
- Last Active Apr 29th 2010
created sub-quasi-category
- Discussion Type
- discussion topicinner fibration
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 29th 2010
split off inner fibration from fibrations of quasi-categories and added remarks on how it models the (oo,1)-version of the notion of cograph of a profunctor
- Discussion Type
- discussion topicCasson invariant
- Category Latest Changes
- Started by zskoda
- Comments 4
- Last comment by DavidRoberts
- Last Active Apr 29th 2010
Casson invariant count SU(2) local systems of integral homology spheres. Thomas considered its holomorphic counterpart which is ultimately related to counting BPS states on Calabi-Yau 3-folds.
P.S. Hmm. Tags. New option. Great. Is there a list of tags ?
- Discussion Type
- discussion topicmicrolocal analysis, D-modules, crystals
- Category Latest Changes
- Started by zskoda
- Comments 17
- Last comment by Tim_van_Beek
- Last Active Apr 28th 2010
I am in a small wave of activity along one of my principal lonegr goals in nlab: the connection between the operator theory and geometry. This is of extreme importance for physics if we ever want to go beyond the TQFTs in quantization program. As Tom Leinster has in his work seen, there are heat-kernel like expansions involved all around the place even when one takes categorical approach and the first terms are of topological nature. This is exactly so in the WKB-expansions where the zeroth term is often the exact value for topological or more general integrable models. Witten's calculation of Witten's index (related to tmf) is an example where such WKB aprpoximations are evaluated and in presence of supersymmetry there are no other terms. Thus I believe that the kantization preferred in nlab is limited to work exactly in simiklar cases and that in general we will have more terms of WKB-like nature involved. We need to develop a categorified WKB method which will unify both.
On the other hand, the WKB method is not just expansion like in quantum mechanics books, it does involve cocycles right away in usual symplectic geometry. There is so-called Maslov index related to the multidimensional WKB method which has been pioneered by V. Maslov. The quantity which is slowly changing is an analogue of the eikonal in geometric optics, so the whole thing is a generalization of the geometric optics approximation. One can see some aspects of that on (free online, on the AMS web site, under books, here) book on symplectic geometry by Guillemin and Sternberg.
Harmonic side of the stationary phase approximation (which is just a variant of WKB in fact) is studied for long under the name oscillatory integrals. This is studied especially by Lars Hörmander and the Japanese school of microlocal analysis (btw, that one is the number 3000 entry in nlab!); the differential equations are often decribed via D-modules and in nonlinear case D-schemes which Gorthendieck described via crystals.
Strangely enough Kashiwara who worked much in microlocal analysis and D-modules has created a notion of crystal bases and crystals of quantum groups but these are NOT related to crystals. Thus I created crystal basis to fix the opinions in the nlab before they go astray...
I created entry hyperfunction, one of the tools of microanalysis, by Japanese school, a neat version of generalized functions, more flexible than distributions of Laurent Schwarz. They are obtained as boundary values of holomorphic functions (reminds me of BV formalism :)).
- Discussion Type
- discussion topic(oo,1)Cat
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 28th 2010
added a section about how to compute limits and colimits in (infinity,1)Cat and in Infinity-Grpd in terms of coCartesian fibrations to these entries.
- Discussion Type
- discussion topicLocally convex space + private web
- Category Latest Changes
- Started by DavidRoberts
- Comments 2
- Last comment by DavidRoberts
- Last Active Apr 28th 2010
I added a bit in the functionals section of locally convex space about coordinate projections being continuous for LCTVSs, and that there are counterexamples to this fact without local convexity. This was from memory, I hope I got it right.
I hope it’s not a fluke that I can edit from home tonight.
I also hyperlinked my front page of my web a bit, as Urs does (like it’s going out of fashion :), so I can present our model to my company, as I (and some others to whom I have explained it) would like to implement the ’open lab book’ research model we have here. I would loove to be able to do it in instiki (by which I mean the technically minded people), but we may be stuck with an awful free wiki platform, chosen for its ’minimal advertising’ (and I quote!).
Anyway, as a result, there are a bunch of new stubby pages there, that probably aren’t worth looking at yet.
- Discussion Type
- discussion topicLatest Changes: Todd
- Category Latest Changes
- Started by Todd_Trimble
- Comments 3
- Last comment by Todd_Trimble
- Last Active Apr 27th 2010
Sharpened up some of the discussion at finitary monad (emphasizing equivalence with Lawvere theories), and added some technical applications to reflexive coequalizer. Both were used to support a detailed proof embedded at smooth algebra.
- Discussion Type
- discussion topic(n,1)-topos
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 27th 2010
expanded the long-time stub entry (n,1)-topos a little more. Made Mike’s former query box an Example-section.
- Discussion Type
- discussion topicAnswer to the query over at structured (infinity,1)-topos?
- Category Latest Changes
- Started by Harry Gindi
- Comments 73
- Last comment by Mike Shulman
- Last Active Apr 27th 2010
Mike left a query box over at structured (infinity,1)-topos about admissibility structures. I am pretty sure that the admissibility structure is not, as the statement in the article says, a grothendieck topology. Rather, it is a class of morphisms that is in some way compatible with the grothendieck topology. At least looking at Toën's notes (which it seems are essentially a version of HAG II restricted to ordinary categories and ordinary stacks (I'm not positive that this is fully accurate, but I'm reasonably confident in the statement)), a geometric structure is a class of morphisms that is compatible with the grothendieck topology satisfying a number of conditions (that seem to match the axioms for an admissibility structure given here!). Correct me if I'm wrong, but it appears that an admissibility structure is precisely the class of morphisms P in the definition of a geometric context (or maybe even the pair (τ,P)).
Here's the link. Anyway, if this is true, it appears to answer Mike's question (once suitably generalized to (∞,1)-categories).
If I'm mistaken, please let me know.
I've put this in the (Latest Changes) category because at the moment, there is no nLab general category.
- Discussion Type
- discussion topiclocal addition
- Category Latest Changes
- Started by Andrew Stacey
- Comments 3
- Last comment by Andrew Stacey
- Last Active Apr 27th 2010
Created local addition to contain the definition and some useful auxiliary stuff. Took a little out of smooth loop space as a seed (for some reason, the extraction got mangled but I think I got it right in the end.)
- Discussion Type
- discussion topicHelp me! I'm trying to understand Bakalov and Kirillov
- Category Latest Changes
- Started by Bruce
- Comments 17
- Last comment by Bruce
- Last Active Apr 27th 2010
- I started a page titled <a href="http://www.ncatlab.org/nlab/show/Help+me!+I%27m+trying+to+understand+Bakalov+and+Kirillov">Help me! I'm trying to understand Bakalov and Kirillov</a> for those (like me) who need help in understanding some of the calculations in this book. I posted my first question. Will try to ask people to answer it.
- Discussion Type
- discussion topicmodel
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 27th 2010
I felt we needed a dedicated entry on model/category of models. So I started one. But just a puny stub so far.
- Discussion Type
- discussion topicsequential colimit
- Category Latest Changes
- Started by Urs
- Comments 7
- Last comment by Urs
- Last Active Apr 26th 2010
ahm, another stupid question: what should sequential colimit point to? directed colimit?
- Discussion Type
- discussion topicunitary morphism
- Category Latest Changes
- Started by Urs
- Comments 3
- Last comment by Urs
- Last Active Apr 26th 2010
I slightly expanded unitary morphism. In particular I added the example of unitary operators.
Then at unitary operator I in turn added the definition in terms of unitary morphisms. I also changed the former link to adjoint to a link to Hilbert space adjoint (since the former points to the categorical notion of adjoint). Also I changed the sentence saying that the unitary operators are the automorphisms in to one saying that they are the isomorphisms.
- Discussion Type
- discussion topicnatural isomorphism
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 26th 2010
edited natural isomorphism a bit more
- Discussion Type
- discussion topicdagger-categories
- Category Latest Changes
- Started by John Baez
- Comments 2
- Last comment by Eric
- Last Active Apr 26th 2010
In preparation for week296 I corrected the definition of dagger-compact category, since it was missing some coherence laws. The most convenient way to include these was to add a page containing Selinger's definition of symmetric monoidal dagger-category . This in turn forced me to add pages containing definitions of associator, unitor, "braiding":http://ncatlab.org/nlab/show/braiding and unitary morphism. Some of my links between these pages are afflicted by the difficulty of getting daggers to appear in names of pages. Maybe a lab elf can improve them.
Hmm, html links didn't work here, so I'm trying textile.
- Discussion Type
- discussion topicorientation in generalized cohomology
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 24th 2010
- Discussion Type
- discussion topicZeidler
- Category Latest Changes
- Started by zskoda
- Comments 3
- Last comment by zskoda
- Last Active Apr 24th 2010
I have moved the personal data on Eberhard Zeidler from QFT entry to his own new-created entry.
- Discussion Type
- discussion topic[[Dmitry Tamarkin]]
- Category Latest Changes
- Started by zskoda
- Comments 1
- Last comment by zskoda
- Last Active Apr 23rd 2010
Dmitry Tamarkin and Gonçalo Tabuada; 2 new references at microlocal analysis.
- Discussion Type
- discussion topicMayer-Vietoris sequence
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 22nd 2010
cerated at fibration sequence an Examples-subsection on the special case of Mayer-Vietoris sequences. From the nPOV, where it becomes a triviality, of course.
- Discussion Type
- discussion topichomotopy BV-algebra
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by zskoda
- Last Active Apr 20th 2010
After having received an email from Bruno Valette I have now at least added a minimum of references to the stub entry homotopy BV-algebra.
- Discussion Type
- discussion topicGaudin model
- Category Latest Changes
- Started by zskoda
- Comments 2
- Last comment by zskoda
- Last Active Apr 20th 2010
Gaudin integrable model as a special case of Hitchin integrable system, and expansion of entry Branislav Jurčo.
- Discussion Type
- discussion topicpseudoalgebras
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Apr 19th 2010
Created pseudoalgebra for a 2-monad as a place to store something I just noticed about normalization, and a related stub at isocofibration.
- Discussion Type
- discussion topicunbounded operator(s)
- Category Latest Changes
- Started by Tim_van_Beek
- Comments 4
- Last comment by zskoda
- Last Active Apr 19th 2010
I made a first draft of a page about unbounded operators, the battle plan contains some basic definitions, explanation of some subtleties of domain issues and what it means to be affiliated to a von Neumann algebra. Right now, only the rigged Hilbert space page refers to it.
- Discussion Type
- discussion topicGray-categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Apr 19th 2010
I added some examples to Gray-category, including also a non-example which has fooled several people.
- Discussion Type
- discussion topicDivision algebras and supersymmetry II
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by zskoda
- Last Active Apr 16th 2010
The nCafé is currently haunted by a bug that prevents any comments from being posted. This should eventually go away, hopefully. For the time being I post my comment in reply to the entry Division Algebras and Supersymmetry II here:
Thanks, John and John for these results. This is very pleasing.
The 3-
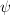 s rule implies that the Poincaré superalgebra has a nontrivial 3-cocycle when spacetime has dimension 3, 4, 6, or 10.
s rule implies that the Poincaré superalgebra has a nontrivial 3-cocycle when spacetime has dimension 3, 4, 6, or 10.Similarly, the 4-
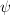 s rule implies that the Poincaré superalgebra has a nontrivial 4-cocycle when spacetime has dimension 4, 5, 7, or 11.
s rule implies that the Poincaré superalgebra has a nontrivial 4-cocycle when spacetime has dimension 4, 5, 7, or 11.Very nice! That's what one would have hoped for.
Can you maybe see aspects of what makes these cocycles special compared to other cocycles that the Poincaré super Lie algebra has? What other cocycles that involve the spinors are there? Maybe there are a bunch of generic cocycles and then some special ones that depend on the dimension?
Is there any indication from the math to which extent
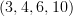 and
and 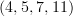 are the first two steps in a longer sequence of sequences? I might expect another sequence
are the first two steps in a longer sequence of sequences? I might expect another sequence 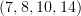 and
and 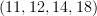 corresponding to the fivebrane and the ninebrane. In other words, what
happens when you look at
corresponding to the fivebrane and the ninebrane. In other words, what
happens when you look at 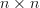 -matrices with values in a division algebra for values of
-matrices with values in a division algebra for values of
 larger than 2 and 4?
larger than 2 and 4?Here a general comment related to the short exact sequences of higher Lie algebras that you mention:
properly speaking what matters is that these sequences are
 -categorical exact, namely are fibration sequences/fiber sequences in an
-categorical exact, namely are fibration sequences/fiber sequences in an  -category of
-category of 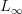 -algebras.
-algebras.The cocycle itself is a morphism of
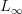 -algebras
-algebras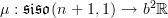
and the extension it classifies is the homotopy fiber of this
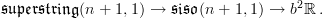
Forming in turn the homotopy fiber of that extension yields the loop space object of
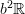 and thereby the fibration sequence
and thereby the fibration sequence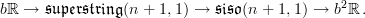
The fact that using the evident representatives of the equivalence classes of these objects the first three terms here also form an exact sequence of chain complexes is conceptually really a coicidence of little intrinsic meaning.
One way to demonstrate that we really have an
 -exact sequence here is
to declare that the
-exact sequence here is
to declare that the  -category of
-category of 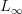 -algebras is
that presented by the standard modelstructure on dg-algebras on
-algebras is
that presented by the standard modelstructure on dg-algebras on 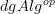 . In there
we can show that
. In there
we can show that 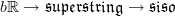 is
homotopy exact by observing that this is almost a fibrant diagram, in that
the second morphism is a fibration, the first object is fibrant and the
other two objects are almost fibrant: their Chevalley-Eilenberg algebras are
almost Sullivan algebras in that they are quasi-free. The only failure of
fibrancy is that they don't obey the filtration property. But one can pass
to a weakly equivalent fibrant replacement for
is
homotopy exact by observing that this is almost a fibrant diagram, in that
the second morphism is a fibration, the first object is fibrant and the
other two objects are almost fibrant: their Chevalley-Eilenberg algebras are
almost Sullivan algebras in that they are quasi-free. The only failure of
fibrancy is that they don't obey the filtration property. But one can pass
to a weakly equivalent fibrant replacement for 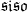 and do the
analog for
and do the
analog for 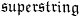 without really changing the nature of the
problem, given how simple
without really changing the nature of the
problem, given how simple 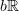 is. Then we see that the sequence is
indeed also homotopy-exact.
is. Then we see that the sequence is
indeed also homotopy-exact.This kind of discussion may not be relevant for the purposes of your article, but it does become relevant when one starts doing for instance higher gauge theory with these objects.
Here some further trivial comments on the article:
Might it be a good idea to mention the name "Fierz" somewhere?
page 3, below the first displayed math: The superstring Lie 2-superalgebra is [an] extension of
p. 4: the bracket of spinors defines [a] Lie superalgebra structure
p. 6, almost last line: this [is] equivalent to the fact
p. 13 this spinor identity also play[s] an important role in
p. 14: recall this [is] the component of the vector
- Discussion Type
- discussion topiclocally presentable category
- Category Latest Changes
- Started by Urs
- Comments 11
- Last comment by Urs
- Last Active Apr 15th 2010
I tried at locally presentable category to incorporate the upshot of the query box discussions into the text, then moved the query boxes to the bottom
- Discussion Type
- discussion topic(oo,1)-category of (oo,1)-presheaves
- Category Latest Changes
- Started by Urs
- Comments 4
- Last comment by Urs
- Last Active Apr 15th 2010
added to (infinity,1)-category of (infinity,1)-presheaves a section on how it is the free (oo,1)-cocompletion
- Discussion Type
- discussion topic(oo,1)-category of (oo,1)-functors
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 15th 2010
added statement to (infinity,1)-category of (infinity,1)-functors on how limits and colimits are computed objectwise - here.
- Discussion Type
- discussion topiccoherence theorems
- Category Latest Changes
- Started by Todd_Trimble
- Comments 3
- Last comment by Todd_Trimble
- Last Active Apr 15th 2010
- As further outgrowth spurred by Sridhar's work on anafunctors and cliques: a stubby start on coherence theorems.
- Discussion Type
- discussion topicCategorified Symmetries
- Category Latest Changes
- Started by zskoda
- Comments 16
- Last comment by zskoda
- Last Active Apr 14th 2010
- Why I can not have this
1. Introduction 3
1.1 Categories and generalizations . . . . . . . . . . . . . . . . . 3
1.2. Basic idea of descent . . . . . . . . . . . . . . . . . . . . . . 5
2. From noncommutative spaces to categories 5
2.1. Idea of space and of noncommutative space . . . . . . . . . 5
2.2. Gel’fand-Naimark . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3. Nonaffine schemes and gluing of quasicoherent sheaves . . . 6
2.4. Noncommutative generalizations of QcohX . . . . . . . . . . 6
2.5. Abelian versus 1-categories . . . . . . . . . . . . . . . . . . 7
but instead I have automatic numbers like 1,2,3, 5, 8 (I know why, but how to avoid it??). I do NOT want nlab to make it like word, I want my numbering to stay it is, and if possible keeping the paragraphs. Putting > for quotation did not help!
- Discussion Type
- discussion topiclocalization of an (oo,1)-category
- Category Latest Changes
- Started by Urs
- Comments 1
- Last comment by Urs
- Last Active Apr 14th 2010
edited localization of an (infinity,1)-category a bit. But more needs to be done.
- Discussion Type
- discussion topiclocally small (oo,1)-category
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by Urs
- Last Active Apr 14th 2010
- Discussion Type
- discussion topicclosed time-like curves
- Category Latest Changes
- Started by Ian_Durham
- Comments 46
- Last comment by zskoda
- Last Active Apr 12th 2010
- Added an entry on closed time-like curves. Also edited a few things in physicscontents in order to clean it up a bit.
- Discussion Type
- discussion topicmainstream mathematics
- Category Latest Changes
- Started by zskoda
- Comments 3
- Last comment by zskoda
- Last Active Apr 11th 2010
I have created in my own nlab, a programmatic entry mainstream mathematics (zoranskoda).
- Discussion Type
- discussion topicLie algebroid theory
- Category Latest Changes
- Started by Urs
- Comments 2
- Last comment by zskoda
- Last Active Apr 10th 2010
in reply to discussion on the blog I
added more details to Lie algebroid
added a reference by Courant to Lie algebroid, Poisson Lie algebroid and tangent Lie algebroid
created Legendre transformation as a placeholder that currently just serves to keep some references on Legendre transformation from the point of view of Lie algebroid theory.
- Discussion Type
- discussion topicautonomous double categories
- Category Latest Changes
- Started by Mike Shulman
- Comments 1
- Last comment by Mike Shulman
- Last Active Apr 10th 2010
I have started to work out a slew of definitions at autonomous double category. Work in progress.
- Discussion Type
- discussion topicobservable
- Category Latest Changes
- Started by zskoda
- Comments 8
- Last comment by Tim_van_Beek
- Last Active Apr 9th 2010
New entry observable wanted at many entries. For now the very basic stuff, with a view toward maximal generality.