nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeMar 28th 2010
<p>In <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7140#Comment_7140">this comment</a>, Mike pointed out a neat little factoid I had never heard before, i.e. an identity morphism is a commuting loop.</p> <p>I am used to thinking of commutative diagrams in terms of TWO paths that start and end and the same objects and the fact the diagram commutes means that composing all morphisms in each of the paths gives an equality.</p> <p>What is the best way to think of a commuting loop?</p> <p>Is the identity morphism the only commuting loop?</p> -
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Oh oh! Got it! :)
Since identity morphisms are present at EVERY object in ANY diagram, regardless of whether they are explicitly drawn, then declaring any loop to commute means it is equal to the identity morphism.
There is something Zen about that :)
-
- CommentRowNumber3.
- CommentAuthorDavidRoberts
- CommentTimeMar 28th 2010
See my comments in the other thread (on functors) - this is usually what a loop can mean, but this is something you have to point out and to me it is a bit of an abuse of notation. What if you want to draw an endomorphism of an object? If you have a category enriched in pointed sets, or even abelian groups say (Like Vect - zero maps are the point), then drawing a single arrow on the page doesn't mean that that arrow is equal to the special arrow that is the point.
I would ask the others if this is a generally accepted convention. I know when I draw diagrams I sometimes take this shortcut, but I don't always like it. -
- CommentRowNumber4.
- CommentAuthorIan_Durham
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
This is an intriguing question, especially to a newbie such as myself. Having discovered that graph theory underlies a lot of category theory, I'm simultaneously working on learning that. So my question would be, how does one categorically represent a graph with one edge and one vertex, which I've always seen drawn as a loop in graph theory? -
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
If you accept that there are identity loops at each object in any diagram, then there is no way around the fact that commuting loops are equal to the identity. The question is, "Are little identity loops implied at each object in any diagram even if they are not drawn?" I would say "Yes", but it would be helpful to define things somewhere one way or the other.
A sensible requirement is that any diagram actually be a category. This is what I always assumed. In that case, for sure, yes, we always have identity loops and any commuting loop will equal the identity.
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
The term "commuting loop" is not a priori well defined. You are proposing an extension of the definition.
For example, what is the degree of the 0 polynomial? It is not a well-formed expression. It is a degenerate case, so we must adopt a formal convention.
What is a basis for the trivial vector space? Again, convention..
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
A sensible requirement is that any diagram actually be a category. This is what I always assumed.
I would say to Ian that this viewpoint is (may?) not be widespread, and possibly misleading. Note also that you cannot cleanly go the other way (unless you grok adjoint functors, and we won't do there in this thread).
@Ian,
I don't know how helpful graph theory is for understanding category theory, because the interesting stuff about categories is the algebra (i.e. composition and other structures). Every category does have an underlying graph, but every vector space has an underlying set - and learning set theory is a long way from linear algebra. In addition, graph theorists have different objectives in mind to category theorists (as do set theorists from people interested in vector spaces).
-
- CommentRowNumber8.
- CommentAuthorIan_Durham
- CommentTimeMar 29th 2010
@David:
Interesting. I agree with you - partly. I'm a visual thinker and the way I was first introduced to category theory made an immediate visual impression in my head so, I think in some senses it can help. I think I could see the same idea with the vector spaces. -
- CommentRowNumber9.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
I came to a point where I thought in diagrams when doing mathematics - at was all diagrams at the time, and a board was essential to even talk about it with anyone. But there is richer structure than just diagrams, which working with examples brings understanding. It is not a flaw since it wasn't designed to, but Awodey's book doesn't treat abelian categories or the like, which were major drivers for category theory in the 50s and 60s.
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
I'm a visual thinker and the way I was first introduced to category theory made an immediate visual impression in my head so
Yep yep. That is an important point. There are various "social circles". Mathematicians hang out with mathematicians. Physicists hang out with physicists. Engineers hang out with engineers. Very few people commingle among the three. John is an outstanding exception. I am also an exception, but to a much lesser degree (I am mortal, John is not :)).
Mathematicians, especially the ones who hang out here, are quite fine with the status quo. Physicists and engineers get tastes, bits and pieces, that this stuff is (or should be) important to them. Some of them are able to make the investment and learn the standard definitions, i.e. "join the n-club" but I can tell you that most in the other social circles, i.e. "scientists and engineers" will struggle with the standard presentations. Even if they are elementary.
Any scientist or engineer can grok a diagram and what it means for a diagram to commute. Diagrams are an important part of any scientist's or engineer's day.
I consider myself to be a poster child for "scientists and engineers". If I can get something, ANYBODY can get it.
I can tell you with a high degree of confidence that a physicist trying to learn category would prefer to see "a functor preserves commuting diagrams" than the standard definition "a functor preserves compositions and identities" even though they are the same (once you've properly defined what "commute" means).
In fact, defining what commute means without circularly relying on functors is doable and I think would be instructive to have in Chapter 1 of "Introduction to Category Theory for Scientists and Engineers" or more colorfully "Radically Elementary Category Theory".
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
Commute.. Isn't that when you take the train to work?
-
- CommentRowNumber12.
- CommentAuthorEric
- CommentTimeMar 29th 2010
Commute.. Isn't that when you take the train to work?
Yes. Yes it is :)
By the way, on my commute this morning, the image of myself in my pin-striped suit hunched over Goldblatt on a train must have been interesting to observe :)
-
- CommentRowNumber13.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
On the train I must, when scribbling in my little black book all the arcane symbols of our field, look a little odd too. Understandable when I was a student, and scruffy looking, but now in business attire... Some of my best work was done on the train. :)
-
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeMar 29th 2010
Scenes from "A Beautiful Mind" come to mind :)
-
- CommentRowNumber15.
- CommentAuthorIan_Durham
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Alas, my train-riding days ended almost seven years ago.
In any case, you will all be pleased to learn that I have returned to Mac Lane (Categories for the Working Mathematician) while still keeping Awodey close at hand.
Incidentally, I have a concrete reason for the graph theory supplement, though. Bob Coecke has developed a semi-graphical description of dagger-categories and I'm trying to figure out the "method behind the madness," as it were.
As for social circles, despite having degrees in engineering, physics, and mathematics, I live in Maine which means my social circle tends to consist of things such as moose, bear, coyotes, and trout. :) -
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeApr 3rd 2010
Identity morphism can cause problems for commutative diagrams.
I am with those who say that if you draw a loop
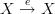 (but not looking like that, since ‘
(but not looking like that, since ‘ ’ should only be written once) and claim that it commutes, then you are claiming that
’ should only be written once) and claim that it commutes, then you are claiming that 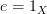 . In particular, an operation on objects and morphisms that preserves all commutative diagrams must preserve identities (and thus be a functor).
. In particular, an operation on objects and morphisms that preserves all commutative diagrams must preserve identities (and thus be a functor).However, not everything involving an identity morphism can actually be drawn in this way. For example, given
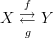 , there's no way to indicate that the composition in one direction is the identity without also catching the other direction. If you tell me that the diagram that I've just drawn commutes, then I'll take it to mean that
, there's no way to indicate that the composition in one direction is the identity without also catching the other direction. If you tell me that the diagram that I've just drawn commutes, then I'll take it to mean that 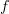 and
and 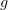 are inverses (although I'll feel more certain if you draw the arrows curved on opposite sides). If you only want one composite to be the identity, then you can either put an identity arrow in explicitly (making a triangle) or adopt a convention that (say) the curved arrow is a section and the straight arrow is the retraction.
are inverses (although I'll feel more certain if you draw the arrows curved on opposite sides). If you only want one composite to be the identity, then you can either put an identity arrow in explicitly (making a triangle) or adopt a convention that (say) the curved arrow is a section and the straight arrow is the retraction.The reason that I'd feel a little uncomfortable taking that diagram literally (to mean that
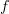 and
and 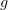 are inverses) is that there's another convention about parallel arrows with no gap between them. For example, if you have
are inverses) is that there's another convention about parallel arrows with no gap between them. For example, if you have 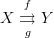 , then to say that the diagram that I've just drawn commutes should mean that
, then to say that the diagram that I've just drawn commutes should mean that 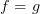 . But in fact, that often appears as a small part of a larger commutative diagram where you don't mean that
. But in fact, that often appears as a small part of a larger commutative diagram where you don't mean that 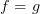 , but simply mean that the diagram commutes with either version. (If you really want to say that
, but simply mean that the diagram commutes with either version. (If you really want to say that 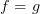 , then again it's better if the arrows are curved on opposite sides.)
, then again it's better if the arrows are curved on opposite sides.)So in a straightforward mathematical theory of commutative diagrams, then you certainly want a loop to be an identity,
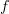 and
and 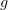 to be inverses in
to be inverses in 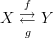 , and
, and 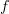 and
and 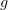 to be equal in
to be equal in 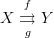 . But in practice, people might adopt conventions that cancel those conclusions.
. But in practice, people might adopt conventions that cancel those conclusions. -
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeApr 3rd 2010
- (edited Apr 3rd 2010)
Commutative diagrams are an informal notation for arguments that could be handled completely formally with a minimal amount of effort. I do not think that there is a sufficiently expressive diagram calculus for modern mathematics to include all of the information in the diagram.
Simplicial sets and quasicategories give us a combinatorial way of formalizing diagram arguments, but it is often impossible to draw the pictures at that point.
-
- CommentRowNumber18.
- CommentAuthorTobyBartels
- CommentTimeApr 3rd 2010
I wrote something at commutative diagram.
-
- CommentRowNumber19.
- CommentAuthorTobyBartels
- CommentTimeApr 3rd 2010
I've redone diagram in accordance with the conversation on this humongous thread which I have read but don't want to reply to.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeApr 3rd 2010
Quivers are directed graphs that allow loops and multiple edges (so they're not really directed graphs), so you can't really equate those two terms (a quiver is a directed multigraph). A directed graph is a much more strict condition.
Also, finiteness is not part of the definition of a quiver, so the comment about finite quivers seems a bit misleading.
Another (albeit much more minor) problem is that the article switches back and forth from "directed graph" and "quiver".
There are three correct terms for the kind of graphs we want to consider: multidigraph (directed multigraph?), quiver, or "Diagram Scheme", which is a term that I've seen and like somewhat (although this usage is restricted to category theory-related stuff). Right now there appears to be a problem where these three identical concepts are given different names on different parts of the nLab.
Question: Which one should the nLab use in general (with exceptions where applicable, obviously)?
-
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Harry, read the discussion at directed graph.
Also, finiteness is not part of the definition of a quiver, so the comment about finite quivers seems a bit misleading.
??? Did you mean to say that finiteness is part of the definition of a quiver (which I would not say, but some people do say that). Because nothing that I wrote should imply that finiteness is part of the definition.
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
That is the wrong definition of a quiver. A quiver is a multidigraph. The free category of a multidigraph/quiver/diagram scheme is just called a free category. I don't understand why we should change this definition from Representation Theory, but we can't change the obviously much worse name of a prestack from Algebraic Geometry. We should be consistent!
The finiteness thing that I noted was at the very beginning of the page. However, the diagram for infinite composition (with or without the cone point) is not finite but very obviously standard.
-
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
A quiver is a multidigraph.
Right. Does it still say different somewhere? (I wouldn't be surprised.)
The finiteness thing that I noted was at the very beginning of the page.
You can't draw it on a page, which is what I was writing about, if it's not finite. But the extension to infinite quivers is pretty natural.
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Sorry, the discussion at directed graph isn't really relevant. I know that there was some discussion about this stuff somewhere; I'll try to find it.
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
At quiver, John decided to take it upon himself to change the definition of a quiver from a multidigraph to its free category. I think we should change the current page over at quiver to free category on a quiver (or on a multidigraph or on a Diagram Scheme), and also change the page called directed graph to quiver (or multidigraph or Diagram Scheme), since a quiver is a generalization of a directed graph.
I see no legitimate reason to change DiGraph->Quiver->Free Category on a Quiver. We should try to use standard terminology unless there is a really compelling argument against it (and in this case, there is not).
-
- CommentRowNumber26.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
Toby #24: There was a ton of discussion surrounding the entry graph, which may be what you were thinking.
-
- CommentRowNumber27.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
@Todd: I think he was talking about the entry quiver, since that was a much bolder (and I think mistaken) change of definitions. The discussion there is also longer.
-
- CommentRowNumber28.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
Let's let Toby decide what he was talking about. Most of the discussion I was talking about was removed, but may be found at version #24, which is linked to in the graph article.
-
- CommentRowNumber29.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
Oh, I didn't know what you meant by #24! I'll check it out right now.
-
- CommentRowNumber30.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Thanks, Todd. I am not sure if the discussion in revision 24 is really what I was thinking of (since I believe that there was discussion on other pages as well, such as what is now graph theory > history, as well as on the Forum and perhaps at latest changes). However, there are some relevant comments there, especially if you search in the page for ‘digraph’.
See also my new discussion thread on the Forum which I made about this issue.
-
- CommentRowNumber31.
- CommentAuthorMike Shulman
- CommentTimeApr 4th 2010
I did a bit of editing at diagram; I think it is looking good. Do we really need commutative diagram to be a separate page from diagram?
-
- CommentRowNumber32.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Well, it would be good to fill in the elementary definition of commutative diagram. For one thing, that would help Harry with his problems with circularity; the definition of functors in terms of commutative diagrams is incomplete so far.
-
- CommentRowNumber33.
- CommentAuthorTobyBartels
- CommentTimeApr 5th 2010
OK, I have put in the elementary definition.
-
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Only now realize what has happened at diagram meanwhile.
I won't have more energy for this, but three brief comments:
I find it not so elegant and not so pedagogical to stat "Definition 1" and "Definition 2" when the second is nothing but a special case of the first.
I see you changed my "poset" to "preorder". In situations where the difference matters, one typically has in the text extra discussion of how the anti-parallel morphisms are to be read as far as commutativity goes. If not the poset interpretation is meant, then what is usually meant is a shorthand for two different commuting diagrams, which are poset images after all.
I had originally made commutative diagram redirect to diagram. I now see that it has been split off as a separate entry, but I don't see that the new separate entry is an improvement over just the redirect.
-
- CommentRowNumber35.
- CommentAuthorMike Shulman
- CommentTimeApr 5th 2010
I already said that I think commutative diagram is better as a redirect to diagram -- does anyone want to speak up in favor of separate pages?
I don't understand your point about poset/preorder. If a diagram commutes whenever any two parallel paths through it are equal, then a diagram with two anti-parallel morphisms commutes when those two maps are isomorphisms, which doesn't necessarily imply that the two objects are equal. So that's a commutative diagram which factors through a preorder but not a poset.
I think one thing that came out of the discussion on diagrams is that the word really is used in at least two different ways, one more restricted than the other. The page could certainly be improved pedagogically, but I think it's helpful to be made aware of this difference.
1 to 35 of 35