nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Question: expressing linear independence in category theory?
Bottom of Page1 to 12 of 12
-
- CommentRowNumber1.
- CommentAuthorIan_Durham
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Suppose there exists a set of matrices, Ak, that are linearly independent (that is, each matrix is linearly independent of all the other matrices in the set). How would one represent such a set in category theoretic terms? (This relates to the particularly sticky problem of how to categorically describe extremal quantum channels.) -
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
You may as well just title your posts "Vague Title"!
-
- CommentRowNumber3.
- CommentAuthorIan_Durham
- CommentTimeApr 4th 2010
Harry: I actually realized that after I had posted it, but then couldn't find a way to change the title of the post. -
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
Click "edit" on the first post, then change title at the top.
-
- CommentRowNumber5.
- CommentAuthorIan_Durham
- CommentTimeApr 4th 2010
Harry: thanks. Didn't think that would allow me to change the title, but obviously it did. -
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
I don't know either, but here are some thoughts to maybe push things forward a small step.
There is a category Vect whose objects are vector spaces and morphisms are linear maps.
There is a category Set whose objects are sets and morphisms are functions.
There is a forgetful functor
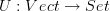
which takes a vector space
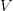 and maps it to the underlying "set" of vectors.
and maps it to the underlying "set" of vectors.Whenever you have a forgetful functor laying around, it is usually interesting to look at its adjoint functor which goes the other way
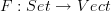
This takes a "set"
 and gives a vector space. In physics/engineering, you'd say the "vector space spanned by
and gives a vector space. In physics/engineering, you'd say the "vector space spanned by  ".
".So the beginning of your question could be rephrased to something like "Say we have a set
 of matrices
of matrices 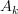 and form the free vector space
and form the free vector space 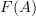 ."
."I'm not sure where to go from here other than maybe to point out that the determinant
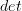 is a functor.
is a functor.Ok. Hopefully an expert can step in now :)
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeApr 4th 2010
A general nonsense formalism, not in the sense of category theory, to bases and linear independence, has been axiomatized by a Bourbaki member Whitney, under the name "matroid". Do we have an entry matroid ?
-
- CommentRowNumber8.
- CommentAuthorIan_Durham
- CommentTimeApr 5th 2010
Apparently we don't have an entry on matroid. I've heard of matroids though. I'll have to look them up.
I like where Eric is going with this, though. Perhaps some sort of composition of the forgetful functor described above and its adjoint could be used to capture the linear independence condition I'm looking for. -
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeApr 5th 2010
Well, just to pick up where Eric left off: suppose
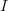 is an index set for a collection of vectors in a vector space
is an index set for a collection of vectors in a vector space 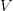 (for example,
(for example, 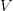 could be a vector space of matrices). In other words, suppose we have a function
could be a vector space of matrices). In other words, suppose we have a function 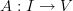 which takes
which takes 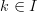 to
to 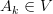 . In other words, suppose we have a function
. In other words, suppose we have a function 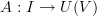 , where
, where 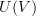 is the underlying set of
is the underlying set of 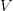 (
(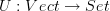 being the functor which forgets vector space structure).
being the functor which forgets vector space structure).Then, by the free-forgetful adjunction to which Eric refers, the function
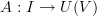 corresponds uniquely to a linear map
corresponds uniquely to a linear map 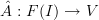 .
.The collection
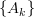 is linearly independent if
is linearly independent if 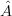 is an injection (a monomorphism); equivalently, if the kernel of
is an injection (a monomorphism); equivalently, if the kernel of 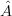 is trivial.
is trivial. -
- CommentRowNumber10.
- CommentAuthorIan_Durham
- CommentTimeApr 5th 2010
So presumably extending this to the collection is relatively trivial as is, perhaps, extending this to . The question is how to check if these conditions hold over a tensor product (functor). -
- CommentRowNumber11.
- CommentAuthorTodd_Trimble
- CommentTimeApr 5th 2010
Could you make this question about the tensor product more explicit?
-
- CommentRowNumber12.
- CommentAuthorIan_Durham
- CommentTimeApr 6th 2010
Sure. So, suppose we show that the set of matrices (or, more appropriately, operators with matrix representation) is a linearly independent set. There are a few specific examples from physics where the set is not linearly independent. The question is if there is a way to check in going from the first to the second, if the linear independence condition holds.
1 to 12 of 12