nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Now that some of us have spent so much time on diagram, would anyone object if I changed:
More generally, a directed graph in a category
 is a functor
is a functor 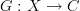 .
.to
More generally, a directed graph in a category
 is a diagram
is a diagram 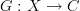 .
.on directed graph.
Edit: I decided to go ahead and make this change. If anyone objects, let me know and I'll roll it back.
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
No, please do not! This is not correct! I've reverted this change.
Please also note that even if the term "directed graph" were correct, it is circular to define it in terms of a diagram (which we defined in terms of quivers (what you've been calling a directed graph))!
This is a major problem. Before these changes were made, the nLab was avoiding circularity by having the notion of a functor defined explicitly. Now the problem with this is that with all of these changes you're trying to make, you're relying on circular reasoning! If you want to use directed graphs and commutative diagrams to define functors, you can not define a directed graph to be a presheaf, which is by definition a functor!
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Harry, The nLab is not Bourbaki, with a foundation chosen once and for all, and every definition built from that in one chosen way. One of the beautiful things of category theory is that it is possible to arrange the definitions in many different ways, and that is what we are doing.
If it were Bourbaki, then we'd have to choose the foundation first!
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
No, but any definition worth adding should _not_ depend on circular reasoning or circular definition chasing. This is not a matter of choosing a foundations. If the page were left how it was, it would not have made any sense to leave Eric's definition over at functor. I assume that since he supports that definition, making it totally circular is not what he intended. -
- CommentRowNumber5.
- CommentAuthorPeter Heinig
- CommentTimeJul 22nd 2017
Expanded directed graph a little. Less (but also) for its own sake, more because I currently had occasion to leaf through my B-J–G tome again. Will stop for today. Hope that a detailed rundown/justification is not required. Would provide one if requested. All mostly terminological. Removed the entry for digraph in the “related concepts” section since it variously could be interpreted as directed graph saying that it is related to itself (which is not wrong of course), or that “quiver” is an instance of directed graph (which is sort-of-wrong). For the definitions, I adopted a mildly informal style. Also, I used colons for the definitions, which seems the right style (and possibly even precisely harmonizable with typing judgments). Intend to extend the article soon, but my main focus is rather understanding and extending the use of planarity in the formalization of pasting schemes.
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeJul 22nd 2017
About the “since” in footnote 1 regarding nLab usage: do you have good reason to believe that? I’m not aware of a discussion where that reason came up.
If I tend not to use “digraph” myself for what I used to call “directed graph” and now often call “quiver”, I think it’s because I figure “digraph” is more likely to be understood in the graph theorist’s sense, and not because of anything to do with the number 2.
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
Yes, and “di-” is very rarely used in category theory to mean 2. The only instance I can think of offhand is dioperad. Also I wouldn’t call “digraph” a portmanteau.
Actually, though, my current impression is that the page directed graph is just a disambiguation page pointing people to either quiver (if they want the category-theorist’s sense) or graph (which discusses all the different kinds of graphs used by graph theorists, including the directed ones). If so, then we shouldn’t add more content to it; any relevant content should be put on quiver or graph, as appropriate.
-
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
I agree that calling it a portmanteau is pushing it, but that is a minor comment.
If you really want to split off material that is pertinent to digraphs in the graph-theorist’s sense, then I myself would have no objection to a new article “digraph”. Right now “digraph” and “digraphs” redirect to directed graph, so those would have to be removed first. My impression is that not many category theorists use the term “digraph” in the quiver sense, but an opening disambiguation sentence could head that off at the pass, just in case.
By the way: Mike recently brought up a couple of times the issue of using footnotes (which have been much in use recently); maybe we could discuss this a little. I’ve sometimes used them too, but maybe we should (re)consider their effect on the reader.
If the intent is not to distract the reader with an aside, then I think footnotes often strangely backfire, calling overmuch attention to themselves (perhaps especially with our software, where they are displayed in normal-sized font right, often sticking out awkwardly below a list of references). In that case it might work better to use a hyperlink as Mike had suggested, where feasible. On the other hand, if you want to use them to make a remark which may be more than a minor aside, maybe it would work better to use a Remark environment (which is used often at the nLab).
-
- CommentRowNumber9.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Many thanks for the comments.
About the “since” in footnote 1 regarding nLab usage: do you have good reason to believe that? I’m not aware of a discussion where that reason came up.
I recognize that you are asking for the reason, not the phenomenon itself, but let me briefly indulge in statistics by mentioning that searching for “digraph” currently yields
9 page(s) containing search string in the page text
while searching for “directed graph” currently yields
76 page(s) containing search string in the page text
and “digraph” has 7 letters, while “directed graph” has 13, so (I resist the temptation to compute decimal fractions now) despite “directed graph” being signficantly longer, it is significantly more frequent (while one would …err… normally? expect an inverse-proportional dependency.)
do you have good reason to believe that?
Thanks for bringing this up. I wrote this because of a mixture of
- a, yes, honest believe on my part that this is one of the—maybe undiscussed or even unconscious—reasons that (can be seen to) explain the above somewhat disproportial preference for “directed graph” over “digraph” at the nLab, a preference that I personally like, mostly for the stated reasons (this is a Pandora’s box, but here goes: sounds like bigraph, there exists more than one sense of 2-graph in combinatorics, and oh, lest I forget, there is also [the orthographical sense](https://en.wikipedia.org/wiki/Digraph_(orthography), and an important sense in the design of programming languages)
- a sort-or-normative intent (slightly biased an experience I once had with this technical term in the course of a course I once gave on digraphs) to remind our readers of, or warn them against, t this particular sort-of-ambiguity of the prefix “di-“. This Latin prefix is used in countless scientific composita (dimer, diploid, etc) to convey two-ness.
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
Personally, I would say that the reason I don’t write “digraph” is purely cultural: I’ve never heard anyone else use it, and it’s not an abbreviation that would have occurred to me on my own. Probably my strongest association with the word “digraph” is actually the orthographic one.
-
- CommentRowNumber11.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Re 7
If so, then we shouldn’t add more content to it; any relevant content should be put on quiver or graph, as appropriate
This is interesting, I will think about it. It is of course a felicitous suggestion, and sort-of-universally-applicable method, that you mention there, namely to use the most ambiguous synonym for a concept as the disambiguation. Here, of the three terms
quiver
digraph
directed graph
it is “directed graph” which is most ambiguous.
Depending on how sort-of-original/sort-of-too-dependent-on serious-use-of-TikZ my treatment of Power’s very interesting proof comes out, I might suggest putting it on the nLab, and then we will have to discuss where to put it and how, and yes, if in Power’s method the use of digraphs sensu stricto turns out to be essential, then it should probably go to a page dedicated to the combinatorial sense.
-
- CommentRowNumber12.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
By the way, sensu stricto is partly
an existing useful slightly-shorter-and-more-abstract version of “strictly speaking”
a semi-jocular pun on the technical meaning of “strict”
which seems useful, when used in moderation.
-
- CommentRowNumber13.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
Todd,
By the way: Mike recently brought up a couple of times the issue of using footnotes (which have been much in use recently); maybe we could discuss this a little.
thanks for starting this discussion. I take this seriously, but will not be able to discuss it now, but hope to return to this soon.
-
- CommentRowNumber14.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
Terminological note: changed “pasting scheme” to “pasting diagram” in directed graph since the previous formulation
giving a rigorous justification of the notational practice of pasting schemes,
had it sort-of-backwards: the “notational practices” are the pasting diagrams, while one of the tools to make them rigorous are the pasting schemes, so the above was sort-of-saying
give a rigorous justification of the notational practice of using one of the rigorous justifications .
Minute technical note: it seems that for a sort-of-empty article like the current version of pasting scheme, the automatic-tolerance-towards the use of plural-s, which otherwise works fine, does not work: if I use pasting schemes then the result looks as if pasting scheme was yet-to-be-created. Note: this issue was not the reason to change to “pasting diagrams”.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
“di-” is very rarely used in category theory to mean 2. The only instance I can think of offhand is dioperad.
We have dinatural transformation. (Not that I think this implies anything, but it came to mind.)
-
- CommentRowNumber16.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
re 15
We have dinatural transformation. (Not that I think this implies anything, but it came to mind.)
This may not imply much but it reminds me of some linguistic issue that I sometimes noted: by and large, the existing naming conventions, in particular the choices between “bi” and “di” make good sense from the point of view of what one might call purity: if the modified word is greek-ish, the prefix tends to be “bi”, if the modfied word is latin-ish, it tends to be “di”: examples: we have bimonoid (not dimonoid, nor diunoid), and yes, we have “dinatural” not “diφύσις, nor διnatural.
Just mentioned for the joy of languages. There surely is much randomness and organic growth in all of this. And I cannot offer much expertise on that point, having only a little (and rusty) formal training in classical Latin. Greeks seem inconsistent by the way, and used both “bi” and “di”. There is διπλό for example.
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
honest believe on my part that this is one of the—maybe undiscussed or even unconscious—reasons that (can be seen to) explain the above somewhat disproportial preference for “directed graph” over “digraph” at the nLab
Thanks for elaborating, but I think such personal guesses are inappropriate and the footnote is a bad idea. Two nLab people have already given you their reasons for not using “digraph”, so that “since” is out of line. Even more grating to me is the “but” coming immediately after, which comes close to suggesting that people at the nLab had (unconsciously?) misunderstood where the “di” comes from. In any case you already explained anyway in the text that it comes from a contraction (which was always obvious to me, but that can stay), so you’re just repeating yourself with that “but”.
-
- CommentRowNumber18.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
re 17:
Good point, thanks. Removed this footnote. It was not written with any conscious intention of adding a guess, let alone insinuating a misunderstanding. it seems an almost self-evident fact, and adding coherence to the page. But, like I said, it has been cut out.
-
- CommentRowNumber19.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
Power’s proof of (I guess you mean) his pasting theorem would probably be very handy to have discussed at the nLab. It would seem to fit at one of pasting diagram or pasting scheme, but less well at an article on some notion of graph I think.
If you could even just write down the precise definitions of these various notions, that would also be very fine in my opinion.
-
- CommentRowNumber20.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Aug 1st 2017)
Re 19: yes I mean the proof in
A 2-Categorical Pasting Theorem, Journal of Algebra 129 (1990)
I am writing an exposition of that. For more than one reason I am not yet sure whether this will be suitable for the nLab.
Having for your made hardly any use of the internet, I sometimes do not realize that there are many degrees of making good use of it. Here, too, there is much more than an all-or-nothing approach.
-
- CommentRowNumber21.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
Yeah, just a little at a time is great. Copying over the definitions you are reading from Power and Michael Johnson would probably be relatively easy, and it would be helpful to others (to me particularly, as university libraries are not an easy convenience to me, and it’s been over 20 years since my head was in any degree pointed in the direction of these particular presentational schemes for higher categories).
Finding a grand generalization of Power’s proof may be a happy by-product down the road, but if it helps to hear: don’t sweat over that vis-a-vis the nLab. As you have surely seen by now, the creation of an nLab article is like sausage-making: sometimes messy, and it can take a while for it to “cure”. We surely don’t expect anything immaculate or polished right away. Even sketches of proofs from those papers (in plain unvarnished English) would be wonderful, if and when you find time for that. No hurry.
-
- CommentRowNumber22.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Re 21: thanks for the feedback. It is less about finding a “grand generalization”, rather about really understanding what Power did, not more and not less.
-
- CommentRowNumber23.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Took the comments of Mike and Todd, (for example those about using directed path to be sort-of-a-disambiguation page, and the one in # 8
would have no objection to a new article “digraph”
for permission to go ahead and start reorganizing and expanding the pages
digraph (newly created)
Please note that digraph has only just been created, and I have to postpone improving it for a few hours now, but intend to return to it soon, mostly with a view towards making it serve the purposes of documenting pasting schemes.
-
- CommentRowNumber24.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
It was not written with any conscious intention of adding a guess, let alone insinuating a misunderstanding. it seems an almost self-evident fact
Don’t take this the wrong way, but if that is true then you really need to adjust your internal awareness of when you are “guessing” and what is “self-evident”. Unless you are telepathic, you cannot know anything about why someone else did something unless you’ve heard them explain their reasons, so any statement about such reasons must be a guess, and cannot be self-evident.
-
- CommentRowNumber25.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
Re #12, to me when I hear someone using phrases such as sensu stricto it sounds as if they are trying to puff themselves up and look erudite. I’m not saying that you are doing that, but I am saying that it sounds to me as if you are. This is especially true when I hear such a person condescendingly explain the meaning of such a term, thereby implicitly assuming that the reader is not as erudite as they are. So in the interests of creating a more positive atmosphere around here, I would recommend that you cut back on the latinisms and comments of this sort and stick to mathematics written in English.
-
- CommentRowNumber26.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
I do agree with Mike’s #25, that this is something to watch out for, and I will have something much more detailed to say soon on various such matters. But I would like to say – gently – that even if sensu stricto is in part wordplay or a pun which privately amuses you, it may come across as a small but annoying distraction to others. Such distractions are cumulative, I can assure you.
I am guilty of using Latin phrases or abbreviations on occasion (and I too am a word-lover; when I was fourteen or fifteen I used to read the dictionary for lengths of time, with fascination). I’ve more recently been rethinking their use. Not long ago I was called out on using “q.v.”, which I’m sure you know, but I was told by my interlocutor that he was sure barely any of his students would know that abbreviation. I sort of got the message. In the past my attitude might have been, “Good! Let them consult a dictionary if they don’t know it; they’ll learn something!” But on further thought, it probably is out of place to play the don that way. We are here for mathematics.
-
- CommentRowNumber27.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
Actually, I sense that not a few of us are fascinated by language(s). I know Toby is, and I certainly sense that Mike is. I know for a fact that Urs and David Corfield are multilingual. So while you may be able to teach us a few things, it might not be as much as you think. ;-)
-
- CommentRowNumber28.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
Yes, I am also fascinated by language. I have little problem with using a word or phrase that the reader may not know if there is a good reason for it, but I don’t think there is usually a good reason to use latinate phrases like “sensu stricto” and (sorry Todd) “q.v.” when there is an equally serviceable English phrase with the same meaning.
-
- CommentRowNumber29.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Thanks for the comments. sensu stricto is simply thought to be a useful sort-of-innovation (it is being used in science). I could launch into giving reasons why, but won’t, not even one, sensing you are not keen on it. (When requested, I would.)
Just one thing: I find it somewhat hurting, probably this is intended, to see Todd say I wanted to teach you (linguistic) things. I had no such idea.
To get back to mathematics, it only now occurred to me, doing my 2-categorical background reading, that there is a rather stunningly relevant-to-this-seemingly-degenerate discussion thing to mention:
C.L.Douglas and A.G. Henriques have a preprint, published since 2012, revised in November 2016, in which
the neologism (in the category theoretical literature, relative to my rather limited experience)
Dicategory
appears, on page 1, in the toc, side-by-side with
Bicategory.
It surprised me to find searches for “dicategory” and “dicategories” yield exactly
0
results in the nLab, despite this preprint’s relative seniority.
So there we have a technical term of the form (latin-ish-prefix,greek-ish term) used by two mathematicians working in category theory.
How worthy-of-documentation “dicategory”, is hard to judge for me.
What do you think, should we create a page
Dicategory
?
(If so, I might take it upon myself to create the page, and document the term.)
-
- CommentRowNumber30.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
I find it somewhat hurting, probably this is intended, to see Todd say I wanted to teach you (linguistic) things.
Whoa whoa – what? I don’t think I said that, and to say I intended to hurt you…
Listen, Peter: I am truly sorry if you got that idea from me, but I intended nothing of the kind.
-
- CommentRowNumber31.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
Let us (mostly) get back to the science please.
-
- CommentRowNumber32.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
Well, not before I tell you that I really resent the accusation that I intended to hurt you; I find it an outrage in fact.
(sorry Todd) “q.v.”
Not a problem.
-
- CommentRowNumber33.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
I don’t think their “dicategories” are worth recording on the nLab; in my opinion a “bicategory with strict associativity” is not an important enough concept to dignify with a name like that. If I had to refer to a bicategory with strict associativity I might call it something like “binary-normal” (identifying the usual category-theoretic notion of “normal”, i.e. having strict units, with “nullary-normal”), although it’s unclear that that’s better than just saying “bicategory with strict associativity” or “weakly unital 2-category”.
By the way, you linked to v1 of their paper instead of the most recent v2; was there a reason for that?
-
- CommentRowNumber34.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
I think I agree with #33, although a little ways up the higher categorical ladder, isn’t there the idea of semi-strictifying tricategories and beyond by retaining weak units and strictifying the higher associativities?
-
- CommentRowNumber35.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
- (edited Jul 23rd 2017)
Well, not before I tell you that I really resent the accusation that I intended to hurt you;
Re 32: This was not meant that strongly, sorry. Or rather, it was not even meant literally, rather an irresponsible choice of words. Sorry.
-
- CommentRowNumber36.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
Re 33:
By the way, you linked to v1 of their paper instead of the most recent v2; was there a reason for that?
Well, yes and no: the version I am studying is v2, but I intentionally went back to the arXiv after my “discovery” this evening, finding it slightly surprising that for four years the “dicategories” had not found their way into any nLab article, to check whether they were there already in 2012. I then without giving it a further thought linked to v1.
-
- CommentRowNumber37.
- CommentAuthorPeter Heinig
- CommentTimeJul 23rd 2017
Will have to leave for today.
-
- CommentRowNumber38.
- CommentAuthorTodd_Trimble
- CommentTimeJul 23rd 2017
Peter: okay then (hand-shake). Thanks. Moving forward, please try to read my posts addressed to you as having benign intentions, and we should be fine.
-
- CommentRowNumber39.
- CommentAuthorMike Shulman
- CommentTimeJul 23rd 2017
Re #34, yes there is, but I would probably name those in a similar way. IIRC Kock called those something like “snu-categories” for “strict no-units”, which I think is kind of reasonable, compared to “dicategory” which doesn’t give any indication of what is meant.
-
- CommentRowNumber40.
- CommentAuthorPeter Heinig
- CommentTimeJul 27th 2017
- (edited Jul 31st 2017)
I took sort-of-a-break from A. J. Power’s proof (which has its subtleties, if taken seriously, and, sadly, if someone would ask me now to fully explain the proof, I could still not do so, but should be able to so soon), and started performing a service which I had been putting off for some time: starting to get directed graph into a fully-informed, innovative, useful, bridgebuilding disambiguation-page-plus. Currently no time to discuss much, yet hope to describe some of the intents and purposes in more detail soon, probably tomorrow.
EDIT three days later: to make the mathematical suggestions and connections to category theory clearer: there are at least two clear things relevant to graph and directed graph, and more generally, to the pursuit of finding good definitions:
to agree upon what the nLab-definition of signed graphs should be, in particular, how to sort-of-categorically define the signs on the edges
to improve the treatment of loops in the context of signed graphs and bidirected graphs; examples of the passage “slightly controversial in the combinatorial literature” in directed graph are
-
- in the paper The flow and tension spaces and lattices of signed graphs, European Journal of Combinatorics 30, p. 266 the authors mention an exception made for “positive loops”
-
- in the paper The flow and tension spaces and lattices of signed graphs, European Journal of Combinatorics 30, p. 272, positively-signed loops are omitted in the definition of the incidence matrix of an oriented signed graph
-
- in the manuscript Resolution of Irreducible Integral Flows on a Signed Graph the authors write
A tricky technical point is that this notation does not distinguish the two ends of a loop; we take an easy way out by treating and as different ends even when . (There are more technically correct means of distinguishing the ends but they make the notation very complicated.)
effectively saying that they resort to an informal technically incorrect formalization. Briefly, this is one example of the shifting definitions that Lawvere seems to be cautioning against in his thoughtful comments at Como.
My suggestion was to find nLab conventions for all this. These notions of sort-of-directed-graphs are widely used, at least in combinatorics, and in my opinion researchers in these fields would appreciate the nLab picking up on this.
-
- CommentRowNumber41.
- CommentAuthorMike Shulman
- CommentTimeJul 28th 2017
This seems pretty unnecessary to me. The page directed graph was intended as a disambiguation page in the sense of Wikipedia, meaning that it consists only of links to the pages that discuss more specific concepts. If you want to write about oriented, signed, or bidirected graphs, then they deserve their own pages, and it seems to me that the place for a comparison of these kinds of graphs is graph. But I’d be interested to hear others people’s opinions.
I do like the phrase “aversion to the void”, though. I kind of want to name an nLab page after it. (-:
-
- CommentRowNumber42.
- CommentAuthorDavidRoberts
- CommentTimeJul 28th 2017
@Mike if Lawvere could be persuaded to use the term…
-
- CommentRowNumber43.
- CommentAuthorMike Shulman
- CommentTimeJul 28th 2017
Why would that matter?
-
- CommentRowNumber44.
- CommentAuthorDavidRoberts
- CommentTimeJul 28th 2017
He’s the sort of person who would take such nomenclature seriously, and use it for an actual mathematical notion (cf being/becoming and other Hegelisms)
-
- CommentRowNumber45.
- CommentAuthorTodd_Trimble
- CommentTimeJul 28th 2017
“Aversion to the void”: sounds like something out of the Tibetan Book of the Dead, as in a description of the fifth bardo state.
-
- CommentRowNumber46.
- CommentAuthorNoam_Zeilberger
- CommentTimeJul 28th 2017
I like the idea of having a “lookup table” describing terminology usage in different references, which is a kind of disambiguation even if it doesn’t follow the usual Wikipedia convention. But perhaps this material could be moved into a separate article with a different title (something like, “Comparison of different notions of directed graph”), which would also be linked to from the disambiguation page directed graph? I’m not sure what would look most natural on the nLab.
Anyways, I have a more specific question/comment about usage. The definitions
- “oriented graph” = “undirected graph together with an orientation on each edge”
- “signed graph” = “undirected graph together with a sign on each edge”
of course make sense for any notion of “undirected graph”, without the need to restrict to simple graphs. How strong is the convention that assumes that the underlying graphs are simple? I notice that this is what they call “oriented graphs” on wikipedia, and they distinguish them from “directed graphs” (“Among directed graphs, the oriented graphs are the ones that have no 2-cycles”). On the other hand, the broader sense of “oriented graph” (allowing the underlying graph to have loops and multiple edges) is used for example in Serre’s Trees, and similarly the broader sense of “signed graph” in Kauffman’s A Tutte polynomial for signed graphs. I guess those two are not graph theorists, but even in Tutte’s Graph Theory, “graph”s are allowed to have loops and multiple edges, and he talks about “orientations” of such graphs (which induce “digraphs” that can have loops and multiple edges).
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeJul 28th 2017
- (edited Jul 28th 2017)
No need to travel all the way to Tibet for this. I’d think horror vacui is due to Aristotle.
(And probably Peter was too afraid to use Latin here, after his recent experiences :-)
-
- CommentRowNumber48.
- CommentAuthorPeter Heinig
- CommentTimeJul 28th 2017
Re 47
(And probably Peter was too afraid to use Latin here,
Yes, I was, and am. Just wrote this in order to avoid the standard Latin term you cite.
-
- CommentRowNumber49.
- CommentAuthorPeter Heinig
- CommentTimeJul 28th 2017
- (edited Jul 28th 2017)
I like the idea of having a “lookup table” describing terminology usage in different references, which is a kind of disambiguation even if it doesn’t follow the usual Wikipedia convention.
Thanks, Noam. I am still thinking how to add more useful features that existing references do not readily offer. One thing such a table (that I plan to extend in due course, there are some inconsistencies) is to tip one over from a state of doubt into certainty, when it comes to working with a text. Of course, only the thing itself can give certainty, but, in my experience such reference-work-like things can speed up the way to certainty.
One small specific example: a precise reference should be given where to find the formalization used in the reference treated in a table, so that readers can check it if need be. In this, a table on the nLab can be quicker than search engines.
Will have to interrupt for today. Hope to get back to the mathematics.
Please note that more or less the main motivation is to do justice, in a careful nLab article, to A. J. Power’s application of a function-symbol-free theory to a function-symbol-using theory. Sadly, I am stuck at a point, but discussing this here would probably create more heat than light, as they say. I should be unstuck soon, there should be something less derivative soon, but personally I think such a disambiguation-page plus has a value and use.
-
- CommentRowNumber50.
- CommentAuthorMike Shulman
- CommentTimeJul 28th 2017
Oh. If it’s a translation of an Latin phrase that has a different standard meaning, then I don’t think we should co-opt it. Better than translating the latin in that case would be to resist the temptation to write it altogether.
-
- CommentRowNumber51.
- CommentAuthorDavidRoberts
- CommentTimeJul 29th 2017
I agree with Mike in #50.
Also, I don’t think an exegesis on cultural differences in mathematics is what is needed at directed graph. Quotes like
It’s very hard to do, you know, a brain dump. It’s very hard to do that.
from Thurston add nothing to the mathematics that would make the page useful.
-
- CommentRowNumber52.
- CommentAuthorTodd_Trimble
- CommentTimeAug 1st 2017
I cut down on the note at the very top, to constrain it to brief description of what the page is and no more. I also took out most of the verbiage under the Zaslavsky quote (difference between “pragmatic” and “epistemological”, the “it should go without saying”, etc.) – the idea being to deliver the goods to the reader efficiently, in accordance with advice at writing in the nLab.
I agree with Noam that the tables may be useful (thanks Peter), but I have no ideas at present about moving them to another article.
-
- CommentRowNumber53.
- CommentAuthorPeter Heinig
- CommentTimeAug 1st 2017
- (edited Aug 1st 2017)
Another purely mathematical step would be:
- to get serious, and eventually reach sort-of-an-nLab-consensus, about the “signature”-column.
It this is done well, this would be something which is offered by no other reference work.
-
- CommentRowNumber54.
- CommentAuthorPeter Heinig
- CommentTimeAug 1st 2017
- (edited Aug 1st 2017)
[In separate comment, for referenceability]
Currently, the only thing which is almost a factual error in directed graph is
- to have written that bidirected graphs are quivers with two additional specified bits of data.
This is sort-of-wrong in the sense that
- this is not the usual way it is done in the combinatorial literature,
while it is sort-of-right in that
(0) this is how I formalized (something simlar to) bidirected graps in an unpublished manuscript of mine, let’s call this specimen of directed graphs “tetradirected graphs”
(1) and: there is a functor from the category of tetradirected graphs to the category of bidirected graphs (in the usual sense).
One should keep (0) and (1) separate; it still seems somehow excusable or even inevitable to have made this mistake, in the sense that if one takes the view that quivers are somehow the best and most flexible graphs there are, then one should start with quivers when formalizing bidirected graphs, in particular when trying to reach an nLab consensus about what bidirected graphs acturally are.
-
- CommentRowNumber55.
- CommentAuthorPeter Heinig
- CommentTimeAug 1st 2017
- (edited Aug 5th 2017)
Towards someday finding an nLab definition of bidirected graph (preferably naturally following from architectual/categorical considerations), in this comment I summarize what I perceive to be the usual definition of bidirected graph in the combinatorial literature.
One reference almost agreeing with this view is Journal of Combinatorial Theory, Series B, Volume 101, Issue 6, November 2011, Pages 464-479.
Why almost: I here allow loops, while loc. cit. doesn’t, for I think this is simpler
The combinatorial literature on bidirected graphs more generally
- evinces an aversion to loops (cf. loc. cit. Introduction, first sentence), partly for a reason.
In this comment I say only so much about the reason for the loop-aversion:
- a functor (bidirected graphs)->(signed graphs), which is useful in particular in flow-theory, seems more problematic to define if the bidirected graphs are allowed to have loops.
This leads the combinatorial literature to make at-least-logically-unnecessary no-loop-hypotheses, or adhoc exceptions, which from a category theoretic perspective appear to make things harder, not easier. I once tried to remedy this, introducing -valued signs (unit group of the Gaussian integers). I do not get into this here, in particular since this seems not to be done anywhere in the literature.
Definition (bidirected graph; using the signature of ZF; using existing nLab notation from pseudograph, and sequent-notation for an implication; perceived by me to be usual combinatorial definition, modulo corrected loop-aversion, and avoiding the minus-sign in the presentation of the sign-set, opting instead for the somewhat-canonical three-element set ).
A bidirected graph consists of the data
- any pseudograph ,
- any function ,
subject to the two axioms
EDIT: caveat lector, the use of the sequent-symbol instead of the logical symbol here is an abuse of notation; the former should be replaced with the latter.
(inns).
(nins).
Remarks
(inns) is for “incidences-non-null-signed”
(nins) is for “non-incidences-null-signed”
is my attempt to take the current definition of “pseudograph” in graph seriously and express “vertex is incident with the edge ” in terms of it. (I recall that an ordered pair in ZF is defined to be the set , hence , hence a vertex is in an edge if and only if . (Note to the occasional person from graph theory happening to read this: you might be used to seeing expressions like , not ;the reason for the latter is that the current nLab article graph strives to define more than only “undirected simple graph”, which nowadays is often defined via two-sets of vertices, by using (quotients of) the product , whose elements are, of course, sets of the form .
- Often, the two non-zero values of are written ’’ and ’’, and, sometimes, they are multiplied (for a purpose), which from a model-theoretic point of view is not possible with the above definition; getting into this would lead away from the remit of the present comment (i.e. to define “bidirected graph”).
- Sometimes, in the literature (cf. e.g. loc. cit. Fig. 1), given a pair of pairs ( , ) with ,
-
- if and , then is interpreted to mean something like
-
- if and , then is interpreted to mean something like
-
- if and , then is interpreted to mean something like
-
- if and , then is interpreted to mean something like
and pictures like this are the reason for names like “bidirected graph” and “half-edge”.
Loc. cit. is vague about what a “half-edge” is exactly; one way to make it precise in terms of the current version of graph is to say “a half edge is a a pair with ”.
Other formalizations of “bidirected graph” can, and perhaps should, be given.
I do not know of any consensus what a morphism of bidirected graphs is. The answer to this might naturally follow from category-theoretic considerations.
-
- CommentRowNumber56.
- CommentAuthorPeter Heinig
- CommentTimeAug 1st 2017
- (edited Aug 2nd 2017)
To give something like a relevant footnote to comment 55, here is a rather typical quote from the combinatorial literature, illustrative of positively-signed loops seen to be a problem and passed over in silence (note that the quote allows at most negatively signed loops)$, and also of a mathematical style which made Lawvere make thoughtful remarks:
A signed graph is simply signed if it has no loops and no parallel edges with the same sign; but it may have two edges, one positive and one negative, joining a pair of vertices. We shall be concerned mostly with signed simple graphs (those with no parallel edges) but occasionally simply signed graphs, and even loops, will play a role.
Usually, negative loops would be allowed; but that is not so suitable to the matrix theory.
-
- CommentRowNumber57.
- CommentAuthorPeter Heinig
- CommentTimeAug 2nd 2017
- (edited Aug 2nd 2017)
In a separate citable comment, relevant material for future terminological discussions:
“directed graph” graph with one-out-of the di2 bits of information per undirected edge having been specified, the choices per edge being independent of one another
“bidirected graph” graph with one-out-of the bidibidi bits of information per undirected edge having been specified, the choices per edge being independent of one another
“tetradirected graph” graph with one-out-of the tetraditetradi bits of information per undirected edge having been specified, the choices per edge being independent of one another
Here,
Definition (tetradirected graph).
A tetradirected graph consists of
data
-
- quiver , given by and ,
-
- function ,
subject to the three axioms
(s-inns),
(t-inns),
(st-nins).
One can be led to think of a choice-of-1-out-of-8 distinct possible pieces of data per edge by counting like this:
- for each , imagine that the set (which for non-loops is a 2-set) has already been agreed upon (intuitively, the underlying undirected graph is taken as a given); it then remains to specify
-
- whether is ensured by or by
-
- the value ,
- the value ,
where the ranges are , not , because of having to comply with axioms (s-inns) and (t-inns).
-
- CommentRowNumber58.
- CommentAuthorPeter Heinig
- CommentTimeAug 2nd 2017
Note to # 57: The sequents (s-inns) and (t-inns) can of course be equivalently written
- (algebraic-s-inns),
- (algebraic-t-inns).
-
- CommentRowNumber59.
- CommentAuthorPeter Heinig
- CommentTimeAug 2nd 2017
- (edited Aug 2nd 2017)
Re 51 : having re-read directed graph recently, I partly agree with David in the sense that
the two Thurston-quotes are the weakest in the article, and, to me,
- the quotes itself—precise renditions from public lectures as they may be—seem to contain too many biological and offensive words, something I seem to have been desensitized to during the editing work for directed graph, but which I now think should be kept out of a reference work)
My suggestion would be to opt for the compromise of
removing the Thurston-quotes
yet leaving in all the Rota-, Lawvere- and the Serre-quotes; they correspond with one another, and hint at some real mathematical issues, and, most importantly, are not about static things like preservation and computerized expert-systems like the Thurston-quotes, but about dynamic and positive things like category theory, style and human understanding, and could lend structure to further development of the article.
Relatedly, in a sense, at the time of Lawvere’s comments, a self-reflecting, critical era within graph-theory had already begun, and on the very topic whose naivete Lawvere is pointing out, for example in view of the long paper
- Friedman, Harvey; Robertson, Neil; Seymour, Paul (1987), “The metamathematics of the graph minor theorem”, in Simpson, S., Logic and Combinatorics, Contemporary Mathematics, 65, American Mathematical Society, pp. 229–261.
I recognize that the above, which perhaps should be added to the references in graph minor, is not about viewing minors category theoretically (loc. cit. does not define morphisms), yet it is a step in the direction of systematization-via-maps and, generally, methods.
-
- CommentRowNumber60.
- CommentAuthorTodd_Trimble
- CommentTimeAug 2nd 2017
I agree with David #51 that the whole of section 7 reads like a lengthy digression and doesn’t fit.
In its current form I’m not sure it belongs anywhere on the nLab. Some of it might be of philosophic concern (if David Corfield is reading this, I wonder what he thinks of that potential), but the wording seems tendentious in places and could come to bite us later. For example, we recently had a spot of public trouble over ’material’ vs. ’structural’ mathematics – which I guess got smoothed over – and there the wording at issue was mild compared to what is now in section 7.
(Side comments: I don’t know what is meant by the ’arithmeticality’ of Serre’s style, nor what ’geometric’ as a contrasting adjective is meant to convey. Not even sure about the use of the word ’semantic’, but I gather it’s supposed to mean something like ’pre-formal’. Also, can’t tell if I agree or disagree with “Model-theoretically speaking, combinatorics rather uninhibitedly expands the signature if the need arises, while category theory is reluctant to do so, and hardly ever does. Category theory prefers to have its constructions preplanned for a given purpose, and carried out by a more uniform method.” The claim about category theory seems a little sweeping and not self-evident, not to me anyway.)
Most nLab pages strive to be factual, disciplined, and with a clear focus. Therefore they will not go into exegeses, disquisitions, extensive stylistic commentary, etc., unless that is clearly warranted.
In the present case, the article starts off being a simple disambiguation, and then it becomes a very heightened disambiguation with large tables, and by the time we get to section 6 it begins to meander off in other directions. To me it looks like the page is seriously in need of an overhaul.
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeAug 2nd 2017
- (edited Aug 2nd 2017)
I think: A plain quote by a well-known mathematician on the topic of a given entry (like Lawvere’s here) does well fit, if maybe in the References-section or in a “History”-section. After all, this is a citation that may be of interest. But what does not fit is an accompanying essay (like the surrounding text there) that claims various completely unrelated quotes by other people into the same context. That’s neither mathematics, physics, nor philosophy, it’s just opinion (moreover opinion claiming to expand on Lawvere’s opinion, which is absurd), and hence off-topic here.
Therefore I vote for keeping the plain quote by Lawvere (the one here) and erase all the rest of that section 7.
-
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeAug 2nd 2017
But that quote should clearly go to graph theory.
-
- CommentRowNumber63.
- CommentAuthorMike Shulman
- CommentTimeAug 2nd 2017
I agree with Urs.
-
- CommentRowNumber64.
- CommentAuthorPeter Heinig
- CommentTimeAug 3rd 2017
I, too, agree with Urs’ suggestions and reasons in #61 and #62. I in particular, agree that the quote of Lawvere’s seems better placed in graph theory.
-
- CommentRowNumber65.
- CommentAuthorTodd_Trimble
- CommentTimeAug 3rd 2017
I removed section 7 and pasted Lawvere’s comments in at graph in a section provisionally titled “Lawvere’s remarks on graph theory (please feel free to retitle or move elsewhere).
-
- CommentRowNumber66.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
In the belief that directed graph is not meant to be a depository for other concepts such as oriented graph, signed graph, etc., I plan to split off some sections to new pages. I have just now created oriented graph (link from Related Concepts in directed graph).
-
- CommentRowNumber67.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Todd, re 66: oriented graphs so far did not have a “section” in directed graph, they just appear in header, table, and related concept list. Splitting off the table entry seems to me to diminish the table’s value (which if anything, should contain more, not less, standardized information side-by-side, to make patterns emerge). All of this seems obvious, and I suppose that you mainly mean the “section” on “Bidirected graphs”, right?
-
- CommentRowNumber68.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Yes they did, Peter.
I’ll take a closer look to see if anything is actually broken in your tables though, and will make any necessary repairs. I wasn’t going to split off the tables, though.
-
- CommentRowNumber69.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
A small related thing, in a separate comment, for referenceability: in my opinion
- the flags in the sense of Kontsevich and Manin, Section 6.6.3, wherein the authors say “A pair{edge, one end of it}is called a flag”, a term which seems to be used in the contemporary categorical literature, should be precisely connected and compared, preferably in the table in directed graph in a suitable format, with the half-edges in the sense of bidirected-graph-theory, like in Section 2 herein. The two definitions seem to be essentially the same, and relating them would seem to increase order.
Does anyone agree with this? And, if so, what should be the preferred nLab term? (To my mind, everything speaks against “flag”: it conjures up a misleading two-dimensional picture, it has another meaning in linear algebra, and in the nLab, and it has another meaning in extremal combinatorics. The term “half-edge”, instead, seems intuitive, and preferable, despite the use of “flag” in papers like the space of string diagrams.
To me this post seems strictly on-topic: “Kontsevich-Manin-flags” are some-sort-of-direction that an edge can be equipped with, so to me the disambiguation page should briefly say something on them, and this post collects relevant information.
-
- CommentRowNumber70.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Along the lines of #66, I’ve created signed graph.
I have temporarily removed the part which said
In a sense, the theory of signed graphs has a signature which contains at least two constant symbols, whereas e.g. the theory of undirected simple graphs (in the narrowest sense) has none.
because I don’t know what sense to make of that. If a signed graph is a structure on a set , then a “constant” in the signature when interpreted in a structure is simply an element of . I took it that in the quoted sentence you (Peter) meant the sign symbols to be constants, but that doesn’t make sense under how constants are standardly interpreted.
In fact, it’s obvious that signed graphs can be construed as a purely relational theory, by positing two relations and on satisfying suitable axioms.
In general, there is a lot of freedom in how one can describe a given class of mathematical objects by signatures. For example, one can (if one wants) replace function symbols by relation symbols that satisfy functionality axioms, and sometimes the reverse is true as well. So “the signature” is not something determined by the category of structures and their homomorphisms, and one should pause to wonder if (or to what extent) signatures need to be set in stone.
-
- CommentRowNumber71.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
So, continuing the thought of #70: to me it would make more sense to have the signature information go under the author table (the second one), because it signifies that author A is using signature X and not signature Y to describe the class of objects. I.e., which signature to choose may depend on the author and the purposes he/she put it to use.
-
- CommentRowNumber72.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
For referenceability, in a separate comment, my suggestion would be
- to add to directed graph, perhaps withing the table, an entry “Borisov-Manin-graph”, with a reference to Section 1 herein.
Does anyone agree to add Borisov-Manin graphs?
A Borisov-Manin graph (B-M-g) is some-sort-of-directed graph, yet the definition is quite different from all the entries in directed graph so far: a B-M-g consists of specified families of, respectively, (0) vertices, (1) half-edges (I am avoiding the authors’ term “flag” here), (2) boundary-map-like-maps, (3) involutions on the half-edge-set.
The term Borisov Manin category of graphs seems to be used quite widely.
-
- CommentRowNumber73.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Does anyone agree to add Borisov-Manin graphs?
Not me.
To repeat myself, directed graph was originally to be a page to disambiguate directed graph in the sense of quiver from directed graph in the sense of digraph. If people use the phrase “directed graph” to mean other things as well, then those things could usefully be mentioned on the page as well (and those things might merit their own pages, just as digraph and quiver do – or they might fit on one of those two pages, depending). But to treat the page directed graph as a grab bag or dumping ground of concepts is not a good way to proceed. That’s my opinion.
-
- CommentRowNumber74.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Re #69: there are surely some things to say about flags and various functorial constructions on various categories of graphs, such as a suitable subdivision functor. Certainly I believe bidirectional graphs could be usefully compared to structures on subdivided graphs. But the placement of this type of material on the nLab should be given some consideration.
On a slightly related note, regarding placement: I’m not happy with the shape of digraph, particularly with the miscellany of concepts. I imagine there are scores, maybe hundreds of individual concepts that appear in digraph theory, but digraph need not and probably should not be a dumping ground for all of them. More useful I think from an nPOV is to outline the most important categorical properties and the most important functorial constructions (e.g., the functor does seem useful, and maybe subdivision merits some discussion). That would help to give the page cohesion. Concepts can be added to a Related Concepts section on an as-needed basis.
-
- CommentRowNumber75.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
(accidentally reposted last message)
-
- CommentRowNumber76.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Re 73: thanks Todd, this is an interesting opinion. I personally thought to do precisely the thing you caution against, just not thinking of it negatively as a “dumping ground”, rather as the most natural and useful place on the nLab for various notions of directed graphs, just because “directed graph” is, to me, so undefined, and it seemed to be foreseeable that users seeing something directed-graph-like might go “hmm, looks like a directed graph, let’s search for ’directed graph’ “. But, again, it is interesting that you think this is not a good idea.
-
- CommentRowNumber77.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Re 74
I imagine there are scores, maybe hundreds of individual concepts that appear in digraph theory, but digraph need not and probably should not be a dumping ground for all of them.
Thanks for this view. This really surprises me since I had taken care ( excepting the currently accidentally mistaken experimental definition of constructive DAG ) to only include what is necessary to conveniently document JAlg129. Please note the sentence
The choice of definitions documented here is biased towards (one of) the uses digraphs are put to in category theory, in particular in giving a rigorous justification of pasting diagrams. The most salient example of this is the emphasis given to plane digraphs in this article.
in digraph. It is a selection made with a purpose (from a digraph-theoretical perspective, it would for example be strange that no notion of higher connectedness of digraphs is covered, digraph-theorists would for example miss Robbins’ theorem, which one can arguably call the first theorem of digraph-theory, but this was not covered since this is not necessary to Power’s proof).
So if we are still aiming at one day creating a good documentation of Power’s Pasting Theorem, like you once seemed to agree, then the “miscellany of concepts” is rather a small select toolbox.
-
- CommentRowNumber78.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
and it seemed to be foreseeable that users seeing something directed-graph-like might go “hmm, looks like a directed graph, let’s search for ’directed graph’
And they should indeed find it there, either via ctrl-F or under Related Concepts.
Possibly I can see an argument that “oriented graph” could redirect to digraph, even though it’s a pretty special case. But “signed graph” is a completely distinct concept, and so is “bidirected graph”. I think one shouldn’t redirect either of those to directed graph, for example.
-
- CommentRowNumber79.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
Todd, Re 74,
one could summarize it thus: I agree that some of the necessary concepts for Power’s proof should perhaps go to the very page pasting scheme, if the proof is documented there, it was just that at the time of writing, pasting scheme did not yet seem to me a fitting place for the notions like king, coking, plane digraph, a-b-path. (Imagine all of these in pasting scheme, with Power’s proof still missing; digraph seems an acceptable temporary place for these notions, and you know, one has to start somewhere.)
-
- CommentRowNumber80.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Re #77: I propose creating Power’s pasting theorem for such a surgical purpose.
nLab pages should be constructed with a bit of thought once they reach a certain length. A page on an important subject like digraph theory deserves a larger point of view than to be a support-system or depository for another envisioned to-be-created specialized page. Thus, it might be wholly appropriate to include an important theorem like Robbins’ theorem on digraph. That’s the type of thing a reader might expect to see. Not a long list of definitions which is mainly for the purpose of a much more specialized theorem like Power’s theorem.
Listen, we’re still jiggering stuff around. It’s a lot of work trying to figure out how to reorganize the definitions sensibly and fit them into a coherent story. My own approach would be to write up Power’s theorem on its own page, and certainly some (brief) mention of this specialized topic would not be totally out of place at digraph. Then we can see what definitions from a Power’s theorem page should be linked elsewhere.
-
- CommentRowNumber81.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
digraph seems an acceptable temporary place for these notions, and you know, one has to start somewhere
That’s where I disagree. The large mass of definitions collected at digraph made for a mess which then has to be sorted through by someone later. In my opinion, the somewhere that one starts at in this case is by writing the relevant mathematics from the bottom-up, at a page where the express purpose is adumbrated in the title.
I think it would be fine for example to state Power’s theorem at pasting scheme (or wherever). If it would be too unwieldy to include the proof there, a separate page can be created for that purpose.
(But even before one starts writing, it would be well to know what one is going to write. Personally, I would try to understand clearly what Powers has done first.)
-
- CommentRowNumber82.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Some remarks on #55:
(1) There was a question raised about defining the incidence relation for a simple undirected graph, given by a pair . The suggestion was to treat these entities as material ZF-sets and use the ZF operation of taking a union.
A structural option would be to view as a quotient, , sending to the orbit of the evident involution . Then define the incidence relation by . (With read as given, this can easily be expressed in the language of finite limits.) You come close to saying something like that under the third bullet of Remarks in #55, except at the end you revert to another ZF-ism about Kuratowski ordered pairs.
(2) The syntax of the definition of bidirected graph looks off. The turnstyle is not a logical connective; it signifies an entailment relation between formulas, and the line
doesn’t quite parse (the quantification doesn’t span across the entailment sign); it should be replaced with e.g.
(But you can also just explain the concept in words without using the symbolism of formal logic. Cf. section 14 of Halmos’s excellent paper on writing mathematics. The picture under the sixth bullet point of Remarks is helpful in getting the idea of bidirected graph across; as earlier mentioned, I think this concept can also be described in terms of subdivision.)
-
- CommentRowNumber83.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
Todd, re #70
because I don’t know what sense to make of that. If a signed graph is a structure on a set , then a “constant” in the signature when interpreted in a structure is simply an element of . I took it that in the quoted sentence you (Peter) meant the sign symbols to be constants, but that doesn’t make sense under how constants are standardly interpreted.
Todd, many thanks for these comments.
Still, I did exercise some “due diligence” (as they say) when I wrote “constant symbols”, and it still seems to me that my use of “constant symbols” was justified, at least by some standard references. I do not see why this is not a standard use of the term “constant symbol”.
Permit me to adduce two usual references, which to have quoted in this thread seems not useless, one from the more model-theoretic literature, the other from the more category theoretic one.
For referenceability, I post two relevant literature references in separate comments.
Please note: I recognize that these posts are not brief, yet they are mostly citations from textbooks, I will clearly mark them as such, so they should be clearly recognizable to be skippable and unimportant to anyone not interested in this particular terminological discussion.
-
- CommentRowNumber84.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Terminological comment, mostly background literature quotes
Todd, Re # 83:
For the model theoretic references, consider the well-known book Hodges, A Shorter Model Theory, First Edition, and therein Section 1.1 “Structures” which says:
A structure is an object [I think with ’object’, Hodges here fait la prose sans le savoir, since categories only rarely appear in his book] with the following four ingredients. (1.1) A set called the domain of , written dom() or dom (some […]). The elements of dom() are called the elements of the structure . […] (1.2) A set of elements of called constant elements, each of which is named by one or more constants. If is a constant, we write for the constant element named .
Apart from the minute terminological issue that I wrote “constant symbol” (which I think even clearer, to mark them out as names) instead of Hodges’ “constant” to refer to the names - and +, it seems to me that Hodges’ definition of “constant” is so permissive as to make my use of “constant symbol” consistent with Hodges’ book: note that he does not require dom() and the set that he calls “a set of elements of called constant elements” to have anything to do with one another, nowhere does he write something like
Constants(A)dom().
Hodges takes ’’ to be nothing else than something of a ’record’, so to speak, that one can apply ’operators’ like dom(.) and ’constants of (.)’ to, and the resulting sets upon applying these ’operations’ need not have anything to do with one another.
Note Hodges does not write ’The elements of are [..]’, rather “The elements of dom() are […]’
Upon reflection, I might agree that these are strangely permissive definitions of “constants, allowing one to call just about anything a “constant symbol”, more precisely, allowing one to simply take any set one likes to be the “set of constants of the structure ”, which indeed seems not very structural.
Yet for the time being I would just like to know whether I overlooked/misapprehended something, on the bare logical/terminological/readingcompetency level.
It seems to me that I didn’t; consider, for additional evidence, e.g. these lecture notes of J.D.Monk tell us
A signature or […] is an ordered quadruple (Fcn,Rel,Cn,ar) such that Fcn, Rel, Cn are pairwise disjoint sets, and ar is a function mapping FcnRel into . Members of Fcn, Rel, Cn are called function (or operation) symbols, relation symbols, and individual constants, respectively. […] The members of Cn are called individual constants. One might think of the function and relation symbols as constants of a different sort. [note that Monk here does not say ’constant symbols’]
Seems completely permissive to me. In particular, neither Hodges nor Monk demand that ’-’ and ’+’ be elements of .
In particular, Monk seems to have decided not to make the connection ’constants are 0-ary function symbols’, as far as I can see from his text. Do you agree?
-
- CommentRowNumber85.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Peter, where Hodges says
The elements of dom() are called the elements of the structure .
He is telling you that “elements of ” means “elements of ”. Thus, when he follows with
A set of elements of called constant elements
he means a set of elements of called constant elements. In other words, a subset .
Yet for the time being I would just like to know whether I overlooked/misapprehended something, on the bare logical/terminological/readingcompetency level.
If you think it meant anything other than what I just said, then I think you really misunderstood.
Where you quote Monk, you should probably examine what he says about interpreting the various items of a signature. (I don’t know what he says, I don’t have the book, but even blindfolded I would ask you to look that up.)
It doesn’t matter a whit that he doesn’t call them constant symbols. I might say “constant symbol” to signify that this is part of syntax, and then I can refer to a “constant” in a structure when interpreting a constant symbol in a structure.
In particular, Monk seems to have decided not to make the connection ’constants are 0-ary function symbols’, as far as I can see from his text. Do you agree?
Not that this seems relevant to what we’re discussing, but:
As I say, I don’t have the book, but I’m certainly prepared to agree, because for some reason, traditional logicians almost never lump in constant-(symbols) with function symbols. To a categorical logician it makes perfect sense to do so, however. Perhaps “aversion to the void” of having as an admissible arity, or some old-fashioned attitude like that. I don’t know.
-
- CommentRowNumber86.
- CommentAuthorPeter Heinig
- CommentTimeAug 4th 2017
- (edited Aug 4th 2017)
Terminological comment, background citations for further possible use in composing tables
Todd,
For the category-theoretic reference, consider P.T.Johnstone: Sketches of an Elephant, Volume 2:
Definition 1.1.1 A (first-order) signature consits of the following data.
(a) A set -Sort of sorts.
(b) A set -Fun of function symbols, together with a map assigning to each -Fun its type, which consists of a finite non-empty list of sorts (with the last sort in the list enjoying a distinguished status): we write to indicate that has type . (The number is called the arity of ; in the case , is more usually called a constant of sort .)
(c) A set of -Rel of relation symbols, together with a map assigning to each -Rel its type, which consists of a finite list of sorts: we write
to indicate that has type . (The number is called the arity or ; in the case , is more usually called an atomic proposition.)
What is wrong with taking this as a licence to define the signature of signed graphs to be the folowing:
Let
-Sort ,
where and are to be taken to be just names for elements of a set, possibly to be interpreted elsewhere according to what their telling names suggest, in particular in proofs in which one need to have some arithmetic structure on the signs (which e.g. can be useful to define the basic signed-graph-theoretic notion of ’odd circuits’ via multiplication, instead of having to resort to an ’IsOdd’-predicate).
-Fun , the anonymous type-assigning map stipulated by Johnstone being the map which
maps to the list ,
maps - to the list ,
maps + to the list .
(Note that the lists are empty here; in particular the arity of both and is .)
and -Rel ,
with being a relation-symbol,
the anonymous type-assigning map herebeing the map which
maps to the list .
The axioms of the theory of signed graphs then should be the four axioms
(irr) ,
(symm) ,
(sign.symm.neg) ,
(sign.symm.pos) .
In particular, - and + here are function symbols of arity 0 hence constant symbols in the sense of Johnstone.
Just for my own peace of mind, setting aside whether one should use ’constant symbol’ in directed graph,
- do you agree that both Hoges and Johnstone give, in their various ways, some sort of licence to call - and + “constant symbols”?
To my mind, this post is to the point; it tries to answer to a question of Todd’s what sense to make of my use of “constant symbols”.
I will have to interrupt for today now.
-
- CommentRowNumber87.
- CommentAuthorTodd_Trimble
- CommentTimeAug 4th 2017
Well, now you’re at least trying to spell out the signature. Before it was really confusing what you had in mind, which is why I asked.
Please note that Johnstone allows multi-sorted signatures, whereas in many logic books they don’t even refer to the set of sorts of a signature; they just refer to function, relation, and constant (symbols). That traditional type of signature could be called “mono-sorted” by categorical logicians. The (Tarski-style) interpretation of the (usually unspoken-of) sort is just this set .
Anyway, let’s see. So you wish to interpret as constants of the sort (I’ll call it )?
Ultimately I think such an approach is doable, but in order to really nail it down, you’re going to have to add more axioms, and the result is going to be cumbersome, and I think people would laugh at it.
The most sensible approach along these lines would have to cut down on the size of so that its only elements are , and some other element which I’ll call . So have exactly 3 constants of sort , and then add an axiom that says , and also axioms . (If you don’t do this, then I think you’re going to have unintended consequences in your models.)
Then have an axiom if – is false, as well as if – is true.
Together with the rest of your axioms.
Personally I think it would be much simpler to go the two relations route, but in summary reply, yes you can define a theory of signed graphs according to your sketched suggestion, a multi-sorted theory which includes two or three constants for one of the sorts and no other elements, but it looks pretty silly to insist on this as being “the signature” for signed graphs.
do you agree that both Hoges and Johnstone give, in their various ways, some sort of licence to call - and + “constant symbols”?
Johnstone: yes, if done right. Hodges – I think I have a copy of his book somewhere, but the answer is again yes if he discusses multisorted signatures or structures; if not, then I don’t see that he’s given “license” in his book, although if he were pressed on the matter in person, I can imagine his giving an airy shrug of the shoulders.
-
- CommentRowNumber88.
- CommentAuthorMike Shulman
- CommentTimeAug 5th 2017
In general I agree with everything Todd is saying. In particular, digraph is not the place for any sort of discussion of Power’s work or of definitions that are specific to it. However, as a slight moderation to #80 I would say that I think it’s okay to create a page A mainly because one needs it to “support” another page B, even if the resulting content at A is somewhat lopsided and incomplete because of the original author’s limited interest in A as a means to B, as long as the content that is placed on the page A is about A in general (e.g. standard terminology and theorems about A, even if a somewhat idiosyncratic choice of such to include) rather than about the use of A in B.
-
- CommentRowNumber89.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
- (edited Aug 5th 2017)
Re 80,
Todd, many thanks for all the comments.
Listen, we’re still jiggering stuff around. It’s a lot of work trying to figure out how to reorganize the definitions sensibly and fit them into a coherent story.
I hear you. I agree.The most substantial issue in all of this seems, to me, that I do not deliver (an exposition of Power’s proof). There are reasons, yet it would be bad style to write about any. I am working to change this; it will take still a little while.
Re
Re #77: I propose creating Power’s pasting theorem for such a surgical purpose.
Re 80:
My own approach would be to write up Power’s theorem on its own page,
This seems to be a good approach.
-
- CommentRowNumber90.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
Todd,
Re 80
A page on an important subject like digraph theory deserves a larger point of view than to be a support-system or depository for another envisioned to-be-created specialized page. Thus, it might be wholly appropriate to include an important theorem like Robbins’ theorem on digraph. That’s the type of thing a reader might expect to see. Not a long list of definitions which is mainly for the purpose of a much more specialized theorem like Power’s theorem.
I certainly agree with this, yet I am surprised to see you see this this way. I take the principle of only adding things which make sense for category theory very seriously, at least as an intellectual exercise, and if I take this view, then I am led to not favoring writing an article on usual digraph theory, rather letting all material included be guided by category theoretical considerations.
However, if, like you at least seem to say, there is a wish around here to include some digraph-theory-style material, then I would be able and glad to do so. (Briefly, this would mean: the usual notions of connectedness, i.e. arc- versus vertex-connectedness, higher connectedness, Robbins’ theorem, the directed Menger theorem, flows). It seems wiser to first try to deliver something presentable on Power’s proof though, yet afterwards I could contribute some of the usual fare.
-
- CommentRowNumber91.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
- (edited Aug 5th 2017)
Todd,
Re 82:
(2) The syntax of the definition of bidirected graph looks off. The turnstyle is not a logical connective; it signifies an entailment relation between formulas, and the line * doesn’t quite parse (the quantification doesn’t span across the entailment sign); it should be replaced with e.g. *
Thanks for catching that. Yes, I simply abused , using it like . Thanks for amplifying that. I will mark my old comment accordingly, to warn inexperienced readers, without hiding the error.
In #86 the sequent notation was correctly used, it seems to me.
Incidentally, you say “entailment relation”. Do you think there is a reason that Johnstone in Definition 1.1.5 of Volume 2 resorts to the circumlocution “[…] a sequent [is] a formal expression […]”, i.e. to the undefined “formal expression”?
Do you think the author is consciously avoiding saying “relation” here?
Probably this is a stylistic/expository decision, to avoid confusion, since he has recently defined “relation symbols” between sorts. It seems to me though, that using a sort called “formula” the author could make into a relation-symbol, literally.
-
- CommentRowNumber92.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
Todd,
Re 70
So “the signature” is not something determined by the category of structures and their homomorphisms, and one should pause to wonder if (or to what extent) signatures need to be set in stone.
Yes, certainly a signature is not a property of a category of structures (in any reasonable sense of “property” that I know of), regrettably perhaps. So, if done badly, listing a signature in a table, can be misleading. I was never meaning to suggest to readers something like “aha, the signature of digraphs is this”, or something like that. Whence the perhaps overly lengthy caveats in the table.
Yet to me it seems advisable to use signatures in directed graph, for pragmatic/systematizing/standardizing reasons. If one tells readers clearly and briefly that the choice of signature is a somewhat arbitray one, but does choose one for each of the variants of directed graphs, this seems, to me, to add structure.
Personally, thinking about signatures helps me to orient myself in the literature.
In my opinion one should simply use the usual conventions from categorical logic, for each of “digraph”, “quiver”, “bidirected graph”, “signed graph”, “Borisov-Manin directed graph”, making some reasonable arbitrary decisions for each, and listing them side by side in the table.
-
- CommentRowNumber93.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
- (edited Aug 5th 2017)
Todd, re 70
In fact, it’s obvious that signed graphs can be construed as a purely relational theory, by positing two relations and on satisfying suitable axioms.
First of all, you are right in the sense that this is often done, sort of, in parts of the literature. A textbook-example is Schrijver’s Trilogy, Volume C, Section 75.2. I say “sort of” because Schrijver’s signed graphs are specified triples with , and with the element of being spoken of as “negative edges” and reasoned about in informal logic, first and foremost, counting the number of members of per cycle and calling those with an odd number of “negative edges” “odd cycles”.
Your definition is, moreover, exactly followed in what is arguably the first paper of signed graph theory, part of which is anticipated in Kőnig’s 1936 textbook.
However (and it seems that Zaslavsky agrees, when writing about Harary’s 1953 paper that “here is the first recognition of the crucial fact that labelling edges by elements of a group-specifically the sign group-can lead to a general theory” [my emphasis])
it seems to me that
- the relational view on signed graphs seems not the right way to go, especially with a view towards category theory.
Reasons:
to me it seems desirable to avoid using unnecessary words and predicates as much as reasonably possible, and instead strive for equational reasoning
if one defines derived notions like “odd cycle of a signed graph”, “balanced signed graph”, and, most importantly for the nLab,
-
- when defining a functor
-
it seems best to have a group structure on the set of signs, and to then multiply signs, and e.g.
- formalize “odd” via “the product is equal to the constant -“.
This then is algebraic/equational reasoning. I am partly interested in doing formal proofs, and
if you use the relational approach, then you have to
- resort to expanding the signature you are working with to finite cardinals (to do the countingof the edges-called-negative), and
- resort to some “IsOdd” predicate in order to formalize “odd cycle”.
Moreover, perhaps more importantly for the nLab, which one day should have a functor
which the combinatorial literature is still lacking,
it seems to me to be true that
the usual map , which
- takes any bidirected graph to the signed graph with defined by , where the minus-sign is one of those arbitrary traditions, and where I resorted to the product-symbol in order to evade issues related to graph having the -function be an unordered pair,
cannot reasonably be defined if you do not have the signs present as part of the signature used (you cannot reasonably define a multiplication on your ), while if you have the and a function symbols, you are free to have ’add-ons’ later.
-
- CommentRowNumber94.
- CommentAuthorPeter Heinig
- CommentTimeAug 5th 2017
Todd, re 87
(If you don’t do this, then I think you’re going to have unintended consequences in your models.)
Do you have any particular “unintended consequences” in mind here? I do not see a reason why the additional axioms
…. axiom that says , and also axioms . (If you don’t do this, then I think you’re going to have unintended consequences in your models.)
if – is false, as well as if – is true.
that you give in 87 are necessary, though I have not yet thought about it yet.
Actually, I do not even type-wise understand what you mean by
The most sensible approach along these lines would have to cut down on the size of so that its only elements are , and some other element which I’ll call .
Please note that in comment 86 I defined ’-’ and ’+’ to be names of elements of the set -Fun, see
-Fun , the anonymous type-assigning map stipulated by Johnstone being the map which
in 87.
More specificall,
- it seems wrong to me to speak of (see 87)
… constants of the sort (I’ll call it ) […] cut down on the size of so that its only elements are , and some other element which I’ll call .
i.e., wrong to speak of a sort having elements. From what I learned,
- “sort” is just a primitive logical concept, or rather, a synonym for “member of the set whose name in the Elelphant is -Sort”.
and, as such, cannot have any elements, nor can you “cut down on [its] size.
Would you please clarify? What definition of “sort” were you using there?
-
- CommentRowNumber95.
- CommentAuthorNoam_Zeilberger
- CommentTimeAug 5th 2017
Re #66 and #46, I’ve expanded oriented graph a bit to include also this more general sense of “oriented graph” (duplicating a bit of content that was already in graph).
-
- CommentRowNumber96.
- CommentAuthorTodd_Trimble
- CommentTimeAug 5th 2017
I may run out of steam responding to all this because I have other things to do, and your comments are numerous and long.
Actually, I do not even type-wise understand what you mean by
The most sensible approach along these lines would have to cut down on the size of so that its only elements are , and some other element which I’ll call .
Obviously I meant that axioms should be added so that in models, where sorts and are interpreted as sets, the set for is to have 3 elements. I think this is a very common type of notational overloading, where the same notation (here ) is used both as a formal symbol and for interpretations of that symbol. Usually the reader should figure out from context which is meant. I do this again below, so be forewarned.
Please note that in comment 86 I defined ’-’ and ’+’ to be names of elements of the set -Fun, see
Yeah, I know. Specifically, they are constant (symbols) of type/sort .
Do you have any particular “unintended consequences” in mind here?
Sure. The set becomes part of the data of what you intend to call a signed graph. Unless the axioms dictate otherwise, in a model, could be a set like where elements other than are irrelevant dross or unintended stuff having nothing to do with the notion of signed graph. Thus you could have two models which look exactly alike as far as all the data that is relevant to signed graphs is concerned, but fail to be isomorphic because e.g. gets interpreted as an infinite set in one and a finite set in the other – differing cardinalities of dross. Thus signed graph isomorphism would not be reflected in model isomorphism.
Anyway, this business about constants seems reasonably cleared up now. It’s good you tell me of generalizations of signed graphs, with edge labelings in more general groups. That does help make this choice of signature seem more natural.
Personally, thinking about signatures helps me to orient myself in the literature.
This may be related to my point that choice of signature varies from author to author, so that that information would better fit the second table by author/reference work.
Do you think the author is consciously avoiding saying “relation” here?
Maybe, I don’t know. I was using the word “relation” informally, at a metalanguage level.
-
- CommentRowNumber97.
- CommentAuthorPeter Heinig
- CommentTimeAug 6th 2017
- (edited Aug 6th 2017)
(Context-adding comment re 70
Along the lines of #66, I’ve created signed graph.
just to add one piece of relevant context for future use in the newly created signed graph: there is some literature on homomorphisms between signed graphs, such as this by Éric Sopena et al.. Note that category theory is absent from that paper, barring one appearance in the bibliography. I do not mean to say that this should be the morphisms of the still-to-be-worked-out category . These morphisms should perhaps be suggested by category theoretical considerations, in particular, by what functors
can be constructed with what definition of morphisms.)
1 to 97 of 97