nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Circular reasoning in definitions
Bottom of Page1 to 30 of 30
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
For those of you who haven't been following, a number of changes have been made to the nLab articles that I am afraid are circular. Previously, the lab had taken the notions of functors and categories to be the fundamental "units" of category theory with which we could define all other concepts. However, if we define a functor in terms of diagrams commuting, we necessarily must define diagrams in a suitable way. However, this requires us to take the notion of a quiver (or multidigraph) and a morphism of quivers (or multidigraph) to be the fundamental "units" of category theory. However, this means that we cannot define them as presheaves of sets on the category with two objects and two morphisms, because presheaves are by definition functors!
I think that as things stand, much of the stuff written is either circular or incorrect. Also, why would we, in category theory, take our "units" to be quivers and morphisms of quivers? The definition of a quiver that does not rely on the definition of a functor is much nastier than the definition of a category (it involves multisets). The objects of study are categories, and the morphisms of study are functors. The whole relationship between categories and diagrams is even described functorially, so I would argue that defining things in terms of quivers is going to implicitly use the adjunction between categories and quivers! This means that we are implicitly using functors anyway. What is the real argument for defining things in terms of diagrams? Eric, your argument that it is easier for engineers and scientists to understand is not an argument that I would agree with, because quivers are nasty to define explicitly. This means that you are hiding all of the machinery of the functor in statements about diagrams that are vastly more complicated than the original notion!
-
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeApr 4th 2010
Hi Harry,
I can appreciate your frustration, but let me try to reassure you that nobody is trying to redefine functors, categories, diagrams, etc with the intention of throwing out the standard definitions. The standard definitions are good ones and will always be displayed prominently on the pages. It's true that I would like to see how far I can get with treating commutative diagrams as the fundamental "units", but this is nothing more than an exercise that I hope will benefit me and possibly other "scientists and engineers". Even if I successfully rewrite Category Theory 101 using commutative diagrams as the fundamental units, we would never replace the standard material. We might supplement it, but not replace it.
My goal is to add knowledge or at least add perspectives. Not take away.
Your points about circular reasoning are good ones and I hope they are only temporary as things work themselves out.
Instead of complaining about it, help us work it out :)
Cheers
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Here, I think that this should explain my dissatisfaction with your new definitions:
Notions preceding a functor in the standard approach:
- Set
- Ordered Pair
- Function
- Category
Notions preceding a functor in the new approach:
- Set
- Ordered Pair
- Function
-Multiset
- Category
- Quiver
- Morphism of quivers
- Commutativity
If you can figure out a way to shorten the second list, I will be very surprised (no, ordered pair cannot go without removing it from the first list as well).
My point is that you're making this much harder than it needs to be. If you understand linear transformations (something that engineers and scientists should be familiar with, no?), it's not much of a stretch to define categories and functors. Another way to say that a functor preserves composition is to say that it distributes over composition in the sense of multiplication!
If we think like Bourbaki for a second, a morphism preserves the structure on a set. Then immediately it follows what a morphism of categories should be.
Another problem: You are basing your definitions on your intuitions about commutative diagrams, but what you seem not to be understanding is that commutative diagrams are harder to define than functors if we want to do so noncircularly. -
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Haven't you ever asked "What if?" :)
What if things had started a different way?
What if category theory had come before Descartes?
What if category theory could be presented purely pictorially as the "language of arrow theory"?
What are the fundamental laws that govern our universe?
What if the universe is a category and these "fundamental units" are actually "fundamental units of the universe"?
What if the diagram
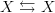
represented virtual particles pairs in the quantum vacuum?
What if the Committee on Laws that Govern the Universe decided that category theory should dictate the laws of nature? Would they stand up there and say "a functor is a map that preserves identities and compositions"? Maybe. I would think they'd have some more poetic way to lay down the laws of nature.
I know I'm being silly here, but I hope you can see my point. I think it is worth examining the basics because I think these basics mean something deeper than they are usually ascribed.
I think your lists are good to think about, but I think they are, to a certain extent, accidents of history. If history had unfolded differently, maybe it wouldn't seem odd that we need to know about quivers before we can talk about functors.
Anyway, I can appreciate that you may not want to help with the project, but I would at least hope you don't try to stand in my way.
If we think like Bourbaki for a second, a morphism preserves the structure on a set. Then immediately it follows what a morphism of categories should be!
See? There we go :) This sounds like another nice alternative way to define functors. Thanks! :)
"A functor is a map between categories that preserves structure." :)
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Yes, this is precisely what the definition of a functor says, in explicit terms. I feel like we can split a functor up into two main ideas: A functor is a map of the underlying geometry of the category that also preserves algebraic structure.
Please be careful, though. I mean that it preserves the algebraic structure of the category itself. -
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Thanks Harry. That is an interesting way to think of it (that I hope finds a home on the nLab!) :)
So this means the "structure" of a category is its commuting diagrams.
[I know you will not like that :)]
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
I think that the only way to develop any intuition for category theory at all is to drop the enriched cases (which have a purely arrow-theoretic description) when you're first starting and assume that all of your hom-sets are honest sets (or algebraic objects in set, so enriching in groups or abelian groups, etc. is alright). The arrow theoretic definitions are nice, but there is a very real sense in which they use the definition in terms of sets as a bootstrap to get off of the ground (for instance, you can't build higher categories without functors in the first place. That would be madness no matter what model of infinity categories you use).
Similarly, trying to abolish the use of set theory entirely (regardless of your choice of set theory (as long as it supports category theory), be it SEAR, ETCS, ZFC+Universes, structural, material, intuitionistic, etc.) seems like a misguided goal.
If you read the discussion over at foundations (or maybe it was at etcs), you can see the problems that one can have defining category theory in the total absence of an ambient set theory. -
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
Harry, I wrote a definition of directed graph (aka "quiver") in nuts-and-bolts terms, which avoids explicit reference to functors. There is no mention of multisets.
I'm not sure why you think we have a serious logical problem with circularity here. On the other hand, one of the things I've always found delightful about category theory is a kind of kaleidoscopic conceptual circularity, where concept A can be understood in terms of concept B which can be understood in terms of concept C which can be understood in terms of A again. This means that there are all sorts of starting places for a reader to begin approaching a concept, and I believe we should be developing this rich interplay of conceptual circles in the Lab.
For example, one very good way to package the concept of internal category in a finitely complete category $C$ is as a monad in the bicategory of spans in $C$ (therefore, an endospan with extra structure -- note that an endospan is the same as an internal directed graph). This may seem circular on the surface, but it should really be thought of as a concise and insightful way of packaging a more nuts-and-bolts definition, one which is richly suggestive of further developments.
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Absolutely, but you need a useful notion of a 1-functor between 1-categories to get anywhere useful. The problem that I have (had?) with the circularity here is that we had direct dependence on the things we were trying to define, which is obviously wrong (morally, of course). That is, we based our definition of a functor on the notion of commuting diagrams, but we were about to define diagrams in terms of digraphs, which were characterized by functors! I feel like the first definition you give after the definition of a category should be the definition of a functor. Working with categories without functors is pretty much just begging for annoyances.
Examples similar to the one you mentioned exist in classical algebra, of course, where just the number of definitions of a module is impressive.
-
- CommentRowNumber10.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
If you think we have any serious problems with logical circularity within the Lab, you should point to them specifically, so that we can fix them. In response to what you wrote above, I did that at directed graph. Anywhere else?
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Nope, you got the one I was worried about. Eric edited one of the pages earlier that I reverted for circularity, which was when I posted this thread.
I think that when we're adding new definitions/etc, we should make sure that the definitions that we're using to construct this definition do not depend on some other formulation of that definition. That is, I urge people who add/change foundational definitions (like functor, diagram, etc) to be very careful to avoid circularity, since it's sometimes hard to spot. -
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
I think your concerns are reasonable, and taking them into account would make for a structurally stronger Lab. Besides avoiding logical circularity, we should also be mindful of readers who don't want to figure out a very slicked-up definition which goes back through a long chain of linked concepts, but want just the facts ma'am. That is: give both the slicked-up conceptual definition, and more nuts-and-bolts formulations, whenever feasible.
Please let us know if you spot such circularity. I'm hoping in all such cases there are easy on-the-spot fixes.
-
- CommentRowNumber13.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
(never mind). -
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeApr 4th 2010
That is: give both the slicked-up conceptual definition, and more nuts-and-bolts formulations, whenever feasible.
Amen. Have a look at 2-category. Huh? Do I really need to know what an
 -category is before I can know what a 2-category is?
-category is before I can know what a 2-category is?How about a 2-morphism? Nope! You need to know what a k-morphism is first. So let's check it out. To know what a k-morphism is, it helps to know what an
 -category is. Deja vu! :)
-category is. Deja vu! :)To be fair, k-morphism does spell out some nuts and bolts, but still. By the way, is the definition at k-morphism restricting things to bigons? What about cubes (my personal favorite shape)?
-
- CommentRowNumber15.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Well... There's something to be said for that.
Let's say that no, you don't need to know what an infinity-category is to understand the definition of a bicategory, but this knowledge does not generalize without passing to the appropriate infinity-case. The list of axioms for a weak 3-category is something like 9 pages long (although I heard that Joyal proved a result that significantly shortens the list of axioms). I don't know if weak 4-categories have been explicitly axiomatized, but I would imagine that doing so would take at least fifty pages (if not far more). This is one of the problems with explicitly axiomatizing weak n-categories called the combinatorial explosion.
Once the appropriate notion of an infinity-category is in place, a weak n-category is as easy to define as a strict n-category, where you enrich over infinity,n-1 categories instead of n-1-categories. So yes and no... -
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
I suspect whoever wrote the article 2-category realized there are two distinct things we mean by that: one is a strict 2-category and the other is what is known by the older term bicategory. The stuff about
 -categories can be read as philosophy which explains why two notions (and then the reader is directed to those two pages). Those two pages seem to me, at a quick glance, reasonably non-circular.
-categories can be read as philosophy which explains why two notions (and then the reader is directed to those two pages). Those two pages seem to me, at a quick glance, reasonably non-circular.I'll see if I can do anything...
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Harry, you might be amused by tetracategory. Not quite 50 pages, but...
Edit: Oops! Yes, there are 51 there (and more work is needed to make the definition absolutely complete).
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Fifty-one pages! Although, I have not actually clicked them, but if you add up the number of pages, it's fifty-one.
Edit: I see exactly why operads are important in an algebraic-type definition of an n-category. They're exactly the right structure to keep track of all of those data. (I can only tell by looking at the little tree diagrams you sketched!) -
- CommentRowNumber19.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
I did a little rewriting over at k-morphism, but it could probably stand a fresh pair of eyes. Please feel free to improve.
Harry: yes, I was pretty directly inspired by operads: the shapes of higher associativities are directly based on associahedra (Stasheff polytopes), and the shapes of the unit data and equations are based on similar polytopes which I call monoidahedra, which I may get around to writing up in the Lab one of these days.
-
- CommentRowNumber20.
- CommentAuthorzskoda
- CommentTimeApr 4th 2010
Limit is a special case of a Kan extension and (pointwise) Kan extension is a special case of a limit. It is a general feature of categorical foundations that everything is a special case of everything to paraphrase George Janelidze. In most of the entries there are multiple ways of definining thing; the nlab does not have an intention to form a linear and complete description of all details. It is sad that people are spending so much effort on polishing trivial issues while there is so little content in many very basic fields of mathematics absent. Like today I noticed that there is no definition of a matroid (basic notion of a whole fundamental theory created in first half of 20th century). Physics is so much absent that it is unbelievable. We do not have such a universal notion in geometry, physics, representation theory, graph theory etc. as it is Laplacian. No Laplacian in nlab. It is destimulating to open the nForum page and seeing that the only discussions going on are about if graph is the same as a quiver or not, when we had the same discussion few times already in last one year. Guys enjoy the discussion if you like, but I want to express that to me, the times when I do not see those nice discussions on infinity bundles Urs has with others but only these issues, I feel kind of missing the interesting part. Is it really that you do not share that feeling of content versus less content ?
-
- CommentRowNumber21.
- CommentAuthorTodd_Trimble
- CommentTimeApr 4th 2010
I appreciate what you're saying, Zoran, and I have these feelings too at times. But sometimes more trivial matters need to be addressed. And polishing can sometimes be a worthwhile and publicly-minded activity.
I am very much interested in putting something up about matroids, but I have also been thinking about other things (and catching up on sleep). Even if I don't know so much about them, they are a fantastic subject. I'd also like to see more physics, but my ability to write about that is limited. Take care -- Todd.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeApr 5th 2010
Zoran, I think you have somewhat unreasonable expectations. You do realize that the nLab is barely a year old, right? And that its focus is mainly on higher category theory? I'm not at all surprised that Laplacians and matroids are missing; in fact I would be more surprised if they were present. I think discussions about proper category-theoretic terminology, and in particular how to choose that terminology to conflict as little as possible with terminology in the rest of mathematics, are at least as much in the spirit of what the nlab is for as would be writing about Laplacians (which have a fairly extensive page on wikipedia already).
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeApr 5th 2010
Guys I am not against clearing up trivial things, I just think that some are carried away by local disturbances away from content-building where it may be also natural for them to contribute. This phenomenon plagued category theorists in history and is one of the principal reasons why say TAC is not included in various databases and why many category theorists leave to other areas at the critical points of their career. People intend to do something with applications in mind, start defering this to future, until they allienate themselves from the original problems. My (mis?)understanding is that Urs cretaed nlab to foster the role (higher) category theory and new foundations have for modern mathematical physics, geometry and topology, and especially with interests in homotopy and cohomology where it does the best. Initial balance at cafe, fostered by John has much more physics. I am not saying this manifesto of connections to "applications", to allienate non-physics inclined people but to remind them of existence of huge empty spaces which are sometimes easy to get growing with some attention. Moreover if we write more widely than it is better chance to attract more contributors to nlab than if we stay some closed community thinking only on pure category theory. Nlab has a chance to contribute to breaking the wall between category land and the wider mathematics community, it would be nice to use that opportunity.
Yes, I am aware that nlab is only one and half years old.
The page at wikipedia is extremely special. The notion of Laplacean exists in much wider contexts including in some parts of discrete mathematics. It leads to conformal field theory, noncommutative geometry, Hodge theory. Hodge theory has ramifications for cohomology of algebraic varieties, not only in characteristics zero. In fact it is pretty central there. Its importance for physics can not be overestimated. For example, Urs was eager at some point to understand the category of mixed motives. But word MIXED points more or less to the wider picture than pure motives, which is in fact extension of the discovery of MIXED Hodge structures of Deligne in cohomology theory. The general thing is that exactly the nPOV is needed to make the picture on, say Laplaceans, clear and wide, and saying that this is not in scope of nlab is in fact giving up the faith in importance of nPOV.
-
- CommentRowNumber24.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
I'd help, but I don't even know what a Laplacian is. -
- CommentRowNumber25.
- CommentAuthorzskoda
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Writing nlab is good to learn it :) Good point to start is to define formal adjoint of an operator on a Hilbert space. Then if you have an operator d in some sort of de Rham complex you look at its formal adjoint d star, and define the Laplacean as (d+d star)^2. Looking at images and kernels, the harmonic forms (those on which Laplacean is zero) split into parts, what leads to Hodge decomposition. This is in very wide contexts. For example, the Casimir operator in a unitary representation of a compact Lie group is sort of Laplacean, it can be written that way and leads to Hodge decomposition. The classical paper of Kostant on Borel Weil Bott theorem (or the one following or before it) has that case for example. Dirac operator comes out from the factorization of Laplacean on a spin manifold (this is the case of Laplace-Beltrami operator on a Riemannian manifold). It tells you all information about the metric, so the definition of Connes of noncommutative manifold starts with a Dirac operator. The spectral picture can be extended to graphs. Over there one has a version of Laplacean and a version of zeta function. Zeta function in many contexts is related to corresponding Laplaceans whose spectra alterantively define the zeta function...
at 7: > If you read the discussion over at foundations (or maybe it was at etcs), you can see the problems that one can have defining category theory in the total absence of an ambient set theory.
It maybe enough to have countable sets to label things, do recursive definitions and so on. Or one may need to have a language of collections of elements, say of families of morphisms. One certainly does not need anything even close to standards like ZF. Joyal had in a parallel discussion an argument with Toby in which he said that one needs some set theory to be able to do categories, and Toby said no and the discussion broke. But what Joyal seemed to mean is that one needs to have some language of finite sets to talk about some families of objects and so on. I mean explain to a person from the Street topos theory and you will see that you very quickly start talking some collections of arrows or something. I do not know what is minimal, but some sense of things like equality of elements in families or collections is certainly kind of set theory in wider and weaker sense, and that one may be needed before starting doing categories.
-
- CommentRowNumber26.
- CommentAuthorzskoda
- CommentTimeApr 5th 2010
and in particular how to choose that terminology to conflict as little as possible with terminology in the rest of mathematics
I agree, in every particular concrete case. But it seems that some of the dicussion is based Eric is questioning the whole edifice of nlab for circularity, where I see multiple paths of defining things are usually present, and the places of missing grounds are gradually being filled in. It is nice that Eric is trying to creatively finding alternatives and provoking us with that. I am just said that when I come to nlab and see no other activity I could connect to but the old boring notion of a functor or things like that. I liked very much a discussion Urs had with Domenico on searching for rather general definition of the Chern character, or of origin of cyclic cohomology. Finding the true mathematical meaning of widely important, while nontrivial constructions with many instances in mathematics and theoretical physics is the most exciting endeavour. This is true certainly also for not well understood but important notions in category theory proper as well.
-
- CommentRowNumber27.
- CommentAuthorEric
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
I liked the conversation between Urs and Domenico also. Now that Urs is back from vacation, I hope more interesting discussions can take place.
The past week or so have been extremely helpful to me personally. I hope I can learn to "walk" and then maybe start contributing something more meaningful. It might have seemed superfluous, but the process I went through was necessary for me to proceed. It's the way my brain is wired. I can never "accept and proceed". It is more like "question, propose, defend, understand, concede, proceed". It's not particularly efficient, but it is effective.
-
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
@Zoran: I am saying that it's much easier to do category theory in an ambient set theory (not ZF necessarily). This was the conclusion that Mike and Toby reached over at the discussion at foundations long before I started posting here. For all intents and purposes, it suffices to base your intuitions on categories defined in an ambient set theory. -
- CommentRowNumber29.
- CommentAuthorMike Shulman
- CommentTimeApr 7th 2010
@Zoran #23, I definitely wasn't saying that the Laplacian isn't potentially in the scope of the nLab. Only that, as we have frequently said, for most of us it is a tool we use more or less selfishly to aid in our research, not primarily an encyclopedic endeavor. But it would be great if it can help to make category theory better accepted, and I do agree that there is sometimes a bit of a tendency to get carried away on small things. On the other hand, I think lack of respect for established notions and terminology is another thing that contributed to the "public relations" problems of category theory, so it's worth taking some care there.
-
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeApr 11th 2010
I agree with all you have said.
1 to 30 of 30