Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration finite foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: diagram

Bottom of Page

1 to 11 of 11

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeApr 5th 2010

    The minute before I had entered offline territory a few days ago, I had expanded the list of examples of (commuting) diagrams at diagram.

    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeApr 6th 2010

    I added a few more, and also improved (I hope) the introduction.

    • CommentRowNumber3.
    • CommentAuthorEric
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

    Edit: Changed this comment to a question.

    Is 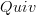Quiv on diagram the category of free categories on graphs or is it the same thing as 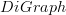DiGraph as defined on directed graph?

    • CommentRowNumber4.
    • CommentAuthorHarry Gindi
    • CommentTimeApr 6th 2010
    I just checked the page, and it means the non-John Baez version of quiver.
    • CommentRowNumber5.
    • CommentAuthorEric
    • CommentTimeApr 6th 2010

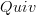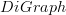    Thanks Harry. That's what I thought. So Quiv and DiGraph mean the same thing.

    • CommentRowNumber6.
    • CommentAuthorDavid_Corfield
    • CommentTimeOct 31st 2017

    We had the definitions of limit and colimit as terminal and initial (co)cones round the wrong way, so have corrected at diagram.

    • CommentRowNumber7.
    • CommentAuthorwillymox
    • CommentTimeJun 12th 2020

    Hi I’m new here. First of all thanks for this great resource you all created. I think there might be a mistake in the component definition of a diagram here. Particularly in the definitions of limiting cone (limit) and limiting co-cone (co-limit). I think it should be stated that the limiting cone is initial among all possible cones and the limiting co-cone is terminal among all possible co-cone. Not the opposite. I might be wrong here, I’m just a hobbyist category theorist ;) Did I misunderstand something ?

    • CommentRowNumber8.
    • CommentAuthorTodd_Trimble
    • CommentTimeJun 13th 2020

    No, it’s right as it is, but I think I can understand why some might find it confusing.

    Take a simple example, where diagrams are over a discrete category with just two objects. If the diagram consists of objects X,YX, Y, then a general cone looks like

    A f↓ ↘g X Y\array{ A \\ \mathllap{f} \downarrow & \searrow \mathrlap{g} & \\ X & & Y }

    The limiting cone is the product X×YX \times Y together with its product projections:

    X×Y π 1↙ ↓π 2 X Y\array{ & & X \times Y \\ & \mathllap{\pi_1} \swarrow & \downarrow \mathrlap{\pi_2} \\ X & & Y }

    and for any cone as in the first diagram, there is a unique map of cones to the product cone, given by a map

    A→(f,g)X×Y.A \stackrel{(f, g)}{\to} X \times Y.

    Thus the product cone is terminal among all cones: terminal means that for any object there exists a unique map to the terminal.

    • CommentRowNumber9.
    • CommentAuthorwillymox
    • CommentTimeJun 13th 2020
    • (edited Jun 13th 2020)

    So we agree, the definition should say it’s terminal, not initial like it is now : over this diagram (def. 2.3) which is universal or initial among all possible cones, in that it ... <– This is from the definition of a limiting cone in definition 2.4, it should say terminal instead of initial. Same for limiting co-cone.

    • CommentRowNumber10.
    • CommentAuthorTodd_Trimble
    • CommentTimeJun 13th 2020

    I see; I was looking at a different part of the page where it was correct. You’re right.

    • CommentRowNumber11.
    • CommentAuthorTodd_Trimble
    • CommentTimeJun 13th 2020

    Fixed definition 2.4.

    diff, v34, current

1 to 11 of 11

  1.