nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeApr 5th 2010
added the full statement to (infinity,1)-Yoneda lemma
It's an easy consequence of the sSet-enriched Yoneda lemma, using the theorem that oo-presheaves are presented by fibrant-cofibrant sSet enriched presheaves.
Notice that this appears without stating the name "Yoneda lemma" as Lemma 5.5.2.1 in HTT. (Beware, though, that there are typos in there. There is a general mix-up of ops already in the statement of the lemma and the first
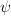 in the proof is a
in the proof is a 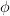 . )
. ) -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
added to (infinity,1)-Yoneda lemma the statement that the -Yoneda embedding preserves all -limits.
Also slightly restructured the entry.
-
- CommentRowNumber3.
- CommentAuthorTim_Porter
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
Just a query, is this a generalisation or related to the homotopy coherent Yoneda lemma that is in the paper I wrote with Cordier: Homotopy Coherent Category Theory, Trans. Amer. Math. Soc. 349 (1997) 1-54? Because of the different context, I was unable to decide.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
Just a query, is this a generalisation or related to the homotopy coherent Yoneda lemma that is in the paper I wrote with Cordier:
All statements in your paper with Cordier will be about -category theory once we have that the homotopy coherent ends and coends that you consider are indeed the relevant kinds of resolutions.
Notably if it is true that your simplicial categories of simplicial functors
are (under homotopy coherent nerve and passing to the core) the correct Dwyer-Kan-hom complexes for the simplicial localization of the category of simplicial categories at the class of Dwyer-Kan weak equivalences, then you are guaranteed that all your statements are indeed about a model for and your Yoneda lemma therefore will be the -Yoneda lemma.
I would be surprised if it were not true that the resolutions that you consider give the correct Dwyer-Kan simplicial resolution. But I haven’t tried to check. Has anyone? Probably by invoking the right theorem about bar resolutions it becomes immediate.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeNov 24th 2010
I didn’t think that simplicial functors and homotopy coherent transformations actually formed an honest simplicial category, since composition of coherent transformations is only associative up to homotopy. I thought you could only make them into some sort of category.
Also, I would normally expect one to need to restrict to the fibrant+cofibrant simplicial categories in order for homotopy-coherent transformations to correctly reproduce the DK-hom-spaces of the category of simplicial categories. The point being that merely using ho-co transformations between simplicial functors does nothing to make sure that all the -functors that should exist from A to B are actually modeled by strict simplicially enriched functors—I expect you would need fibrancy+cofibrancy of A and B for that.
However, if you restrict things in that way, then I would expect the homotopy coherent Yoneda lemma to be equivalent to the (∞,1)-Yoneda lemma.
I also think it’s relevant that in Categorical strong shape theory, M. Batanin showed that coherent transformations can be used to give a model for the “homotopy bicategory” of sSet-Prof obtained by inverting the (2-cell) levelwise weak equivalences of sSet-profunctors. In fact that bicategory should be a proarrow equipment on sSet-Cat, and inside any proarrow equipment there is a Yoneda lemma that comes for free. That Yoneda lemma should also be a model of the (∞,1)-Yoneda lemma.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
I didn’t think that simplicial functors and homotopy coherent transformations actually formed an honest simplicial category,
Ah, thanks, I had not been aware of that.
Also, I would normally expect one to need to restrict to the fibrant+cofibrant simplicial categories in order for homotopy-coherent transformations to correctly reproduce the DK-hom-spaces
Hm, if that is really necessary then the use of homotopy coherent transformation would be small: for passing to a cofibrant replacement of the source is already a major “homotopy coherence”-step. I would have hoped that this is the kind of resolution that is implicitly accomplished by a homotopy coherent end calculus.
For instance we know that since the model structure on is combinatorial, it is equivalent to a simplicial model category structure. If we pass to that, then cofibrant+fibrant replacement is all there is to do and no further resolved ends are necessary.
(That’s just an observation, not an argument that this route is really simpler. But it makes me wonder.)
-
- CommentRowNumber7.
- CommentAuthorTim_Porter
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
Batanin’s nice paper used more or less the same machinery and produced what we thought of as an A_infty cat. The idea was already in Vogt’s work. I think it has some pedagogic value as an approach. My feeling, and memory, is that there was a span (anafunctor?) of actual simplicial things, using the rectification process that generalised Street’s.
I have not known how to encorporate some of this into the Lab . I found the texfile of the paper this morning whilst looking for something else, so perhaps it can be useful, but it hit problems because of one or two lacks of insight that had to wait for others to provide them.
Our idea was to use actual homotopies whenever possible, so as to avoid weak equivalences until the last moment. We got quite far, and I liked that approach. In more modern parlance, we used fibrant and/or cofibrant replacement plus homotopies to get the necessary step.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
Which result by Batanin are we talking about, precisely?
I guess one in
Homotopy coherent category theory and -structures in monoidal categories (pdf)
?
So there is an --category . That’s fine with me. Do we have a good notion of simplicial nerve of that (hm, I should know that, but right now I don’t)? If so, did anyone try to compare its homotopy type to the correct Dwyer-Kan space ?
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
hm, I should know that, but right now I don’t
I do: by the rectification result every --category is -equivalent to a strictly associative -category. Pass to that and take the ordinary homotopy coherent nerve.
-
- CommentRowNumber10.
- CommentAuthorTim_Porter
- CommentTimeNov 24th 2010
Suppose that is fibrant (locally Kan), then a h.c.diagram is a simplicial map from Ner(A) to Ner_{hc}(B), and the nerve of Coh(A,B) should be the corresponding function complex of maps from Ner(A) to Ner_{hc}(B). That corresponds exactly to the structure one would want, but will probably only be equivalent to the Dwyer-Kan one, of course that is to be expected.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeNov 24th 2010
The issue as I see it is that since sSet-Cat is a 2-category, there are two different kinds of homotopy-coherence. On the one hand, for simplicial categories A and B, we need A to be cofibrant and B to be fibrant in order for all (∞,1)-functors A→B to be represented by honest simplicial functors A→B. On the other hand, for two functors F,G:A→B, we would need F to be cofibrant and G fibrant “as functors” in order for all (∞,1)-natural transformations F→G to be represented by honest simplicial natural transformations F→G. However, for general A and B, there may not be a good model structure on the category of simplicial functors A→B. Instead, we can look at coherent natural transformations to get a good model for the (∞,1)-category of functors A→B. But this doesn’t do anything about the problem of needing A and B to be (co)fibrant in order for all the functors to exist that should.
Maybe that is obvious, but I thought someone should say it explicitly.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
since sSet-Cat is a 2-category
That is a plausible reason for the role of a two-stage resolution.
On the other we know that it is possible also to get away with just a single-step resolution, at least if we want as an -category, which is sufficient to get say the -Yoneda lemma: we know that there is a simplicial model structure on that presents . And in that a single-step resolution is evidently sufficient.
In any case, somebody still has to work this out, it seems. It is very plausible that applying homotopy coherent transformations between fibrant+cofibrant resolutions in presents (probably then even as an -category). But how would we go about proving this?
Did nobody consider something like this before? What were the design criteria for the definitions in homotopy coherent category theory? It must have been checked against something, I guess?
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 2nd 2011
added to (infinity,1)-Yoneda lemma a proposition that in lack of a name I called Local Yoneda embedding (maybe not the best term).
1 to 13 of 13