nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeApr 6th 2010
I think that, given a (noncommutative) differential graded algebra
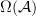 over a commutative algebra
over a commutative algebra 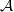 , we can obtain a directed graph.
, we can obtain a directed graph.We can do this (I think) by associating a directed edge to each element of degree 1 (I'll call it a 1-form)
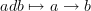
This smells like a forgetful functor
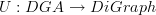
As far as I can tell, the only obvious thing to do when someone hands you a forgetful functor is to form an adjunction so that we talk about a "free differential graded algebra on a directed graph"
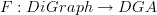
If this makes any sense, then I think I just summarized about half of Urs and my paper in that one statement. In the paper, we did this in explicit gory detail.
There are special commutative algebras that are particularly neat for doing this kind of stuff.
Under what circumstances does a commutative algebra admit a complete set of projections
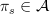 ? I define a complete set of projections by the relation
? I define a complete set of projections by the relation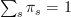
and

where
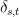 is the Kronecker delta.
is the Kronecker delta.I called an algebra that admits a complete set of projections an algebra of projections (ericforgy) (imagine that!). Is there a standard term for such a thing?
An algebra of projections provides a convenient basis for a noncommutative DGA and we have
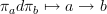
and the projections can be interpreted as the nodes of the directed graph.
I hope that with something like this, all the algebraic gymnastics we performed can reduce to a simple wave of the adjunction wand. Am I dreaming?
Does this ring a bell for anyone? I would appreciate any pointers to references on similar ideas.
Thanks!
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeApr 6th 2010
Systems of primitive/orthogonal idempotents/projectors are a standard topic in the study of rings, look at classical topics like artinian rings, Wedderburn theorem, matrix rings, Morita etc.
A-infinity algebras can be introduced in the language of k-linear quivers, or of k-linear cocategories. See the approach by Lyubashenko.
-
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeApr 7th 2010
Thanks Zoran. I hope I can connect the dots (although it is probably obvious) between what I'm trying to describe here and dg-quiver. I'll have another look at Lyubashenko, but it seems a little heavy.
1 to 3 of 3