nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: path category vs cobordisms for bundles
Bottom of Page-
- CommentRowNumber101.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 16th 2010
Urs,
no need to apologize, I was joking :)
(yet looking forward to seeing you back here)
-
- CommentRowNumber102.
- CommentAuthorUrs
- CommentTimeApr 16th 2010
Okay, I am on the train back home. Time to get something done! :-)
Here is a thought that migh serve to interpolate a bit between some things that have been said:
We want for
our target space object;
our background field
our parameter space cobordism
the quantum propagator along such in the most abstract-nonsense way.
The action functional on the space of fields is the induced morphism
,
where angular brackets shall denote the -groupoid valued hom. (In lack of a boldface .)
Let’s further postcompose this with passing to cohomology
.
I assume now for definiteness for the moment that is closed and that the cohomology on the right is , by integration without integration. Then we get a total morphism
.
This is an -groupoid over , that happens to be just a groupoid over . So we are entitled to the -groupoid cardinality of it. This is precisely the DW-invariant of :
the sum over iso-classes of of their value in under times one over the automorphism of the iso-class.
Do you see what I mean?
Now consider the case with nontrivial and …
-
- CommentRowNumber103.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 16th 2010
perfect. and what is most important, totally irrelevant to which model for one chooses (nice topological spaces, oo-groupoids,…)
now, the case with nontrivial and . according to the relative cohomology prescription we have been discussing/suggesting above, the only change should be in passing to cohomology. this time we should have
assuming that is connected the cohomology on the right is again , and taking oo-groupoid cardinality ne recovers DW receipt for the matrix elements of the 1-morphism associated with .
next step, a clean nonsense description of the vector spaces associated with and . these should be described in terms of sections of the -bundles associated with flat -bundles on and sketched in #95
-
- CommentRowNumber104.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 18th 2010
a few lines on the top-dimensional part of the Yetter model. the abstract nonsense works so well that it’s just copying and pasting from Urs #102 above, with the changes for and for . as usual, I’ll be topological (one swithces to the groupoidal version by writing \mathbf in place of \mathcal and in place of ). so, for a given finite strict 2-group , let be its homotopy type. fix a background field , and let be a (closed, compact, oriented) -manifold. The action functional on the space of fields is the induced morphism
,
where angular brackets denotes the -groupoid valued hom. one further postcomposes this with passing to cohomology
.
and gets a total morphism
.
This is an -groupoid over , that happens to be just a 2-groupoid over . indeed, since is a 2-type, so is ; this can be easily seen, e.g., as follows: . the -groupoid cardinality of over is the Yetter invariant of .
one can explicitly compute it using a combinatorial (i.e. groupoidal) model, e.g., taking a trinagulation of . since this will be just a way of computing an intrinsic object, the result will be manifestly independent of the triangulation chosen.
-
- CommentRowNumber105.
- CommentAuthorUrs
- CommentTimeApr 19th 2010
- (edited Apr 19th 2010)
Domenico,
sorry for not getting back to you earlier, I was forced offline after my last message here and then was distracted all weekend by family matters.
one recovers DW receipt for the matrix elements of the 1-morphism associated with Σ.
Yes, I had meant to type this, but it is kind of clear.
next step, a clean nonsense description of the vector spaces associated with and . these should be described in terms of sections of the -bundles associated with flat -bundles on and sketched in #95
Yeah, something like this. There ought to be a very systematic way to go about this…
-
- CommentRowNumber106.
- CommentAuthorUrs
- CommentTimeApr 19th 2010
Domenico,
much as I am fascinated by the discussion we are having here, you should know that I will have to refocus my attention for a bit for a few days. Right now I am on my way to Regensburg, where I meet Ulrich Bunke this week. We will talk about infinitesimal and finite path oo-groupoids and differential cohomology, and so I need to concentrate on that for the time being.
I dearly hope, though, that we can come back to discussion of the quantization step, a little later on. I would still ike to advertize the idea that there ought to be a systematic way to include all the things that have been said here into one uniform picture in which the total space of the background field bundle plays a central role, but I need more time to spell this out in more detail than I have right now.
-
- CommentRowNumber107.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 19th 2010
Urs,
no need to apologize, really.
I’m now thinking of the use of loop space functor in these constructions. this is clearly inspired by your preprint with Zoran, where you make the following really interesting remark: consider and as pointed spaces and transgress the background field to loop spaces. what you get is (up to homotopy) . clearly, in the naive form I’ve just presented it, this is an highly noncanonical construction, since there is no preferred choice for basepoints. but then we can easily make it canonical by choosing all basepoints at once: over we have a canonical -bundle: the universal -bundle , which up to homotopy is the paths bundle of . in other words, up to homotopy is the bundle whose fiber at is the based loop space . similarly, over we have a canonical -bundle . transgression of maps a based loop at to a based loop at , so is a canonical bundle morphism .
-
- CommentRowNumber108.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 19th 2010
- (edited Apr 19th 2010)
let me add another tiny tessera to the kantization mosaic we’re trying to compose here: let be any group and let be its delooping. then . a linear representation of is a functor and we can push this forward along the projection to isomorphism classes by taking the right Kan extension of
this is precisely -invariant elements of .
-
- CommentRowNumber109.
- CommentAuthorzskoda
- CommentTimeApr 19th 2010
- (edited Apr 19th 2010)
Urs, if you are going to Regensburg, remember that Ulrich Bunke has several papers on eta invariants, zeta functions and so on, so he is the right person to talk to connect the picture discussed in this entry with the more fundamental origin of the anomalies at the level of renormalization. BTW today on the arXiv there is a related paper by Lisa Jeffreys.
Domenico, as fr as your consideration of zeta function regularization as non-fundamental, I should refer you to the picture of the paper of Tamarkin on renormalization which is unfortunately just the first of an ubruptly left series of works (the partial results he got on nonlinear sigmamodels will never appear, and he left the problematics); in Tamarkin's picture the zeta function regularization is one choice of a homotopical resolution. All resolutions are equivalent of course, and there is a group of automorphisms among the resolutions, in fact a torsor. If we restrict to a subclass than this is more or less the generalization of Connes-Kreimer Hopf algebra which should be a function algebra on one of such affine groups, corresponding to the torsot with a choice of base point.
-
- CommentRowNumber110.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 20th 2010
Zoran, that’s exactly what I meant: zeta function regularization should be a way of computing something more intrinsically defined. thanks a lot for the reference. you’re referring to “A formalism for the renormalization procedure, math/0312219”, right?
-
- CommentRowNumber111.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 20th 2010
- (edited Apr 20th 2010)
generalizing slightly #108 above, given a flat vector bundle , one can define the vector space of -equivariant sections as the set of sections such that for any path from to . then the pushforward (right Kan extension)
is a collction of vector spaces indexed by elements in the set . pushing still forward along , one gets a single vector space: the vector space of equivariant sections of .
-
- CommentRowNumber112.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 20th 2010
- (edited Apr 20th 2010)
assume now we have two topological spaces and and two flat vector bundles and . denote by and the equivariant sections of these bundles, and let be a morphism which lifts to a natural transformation . then, by the universal property of right Kan extension we have an induced natural transformation , i.e. a linear map
-
- CommentRowNumber113.
- CommentAuthorUrs
- CommentTimeApr 20th 2010
the vector space of equivariant sections of .
Where -equivariant means: flat! Yes.
-
- CommentRowNumber114.
- CommentAuthorzskoda
- CommentTimeApr 21st 2010
Yes, it is that preprint of Tamarkin (pretty hard to read, it assumes familiarity with the preliminaries in Beilinson-Drinfeld). I somewhere have handwritten writeups of few lectures of Tamarkin beyond that material. Namely this first lecture is just for deformation of the free theory in 4 dim. The main prupose was preinrt #2 which was abandoned where nonlinear Poisson sigma model of Kontsevich-Cattaneo-Felder was to be discussed as well as some cute things like showing that topological sigma models A and B (from mirror symmetry business) are derived Hamiltonian reduction (concept due Tamarkin, unpublished) of the former: the data fro the reduction were geometric. Everything boils down to the singular behaviour of D-modules, what is to be expected. The singular behaviour of solutions of differential equation is all what matters in field theory in a way of thinking. Tamarkin somehow got disappointed with his original aspirations in this business and left the project. Now Costello is doing renormalization with another kind of homotopical resolutions formalism, with less D-modules and Tamarkin told me he likes it. However, Costello is doing a limited case, which does fit with approaches mainstream theoretical physics, but it is only about the perturbation of quadratic potentials and does not really do deformation theory of field theories around an arbitrary vacuum; one can not consider any theory a deformation of free theory (the classical QM tricks like interaction picture are of no use to cure this problem, the generality of the geometry of, say, vacuum propagators to be deformed is really a limiting factor). This is a bit surprising having in mind that he had works in CFT which is a different case from that point of view.
-
- CommentRowNumber115.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 22nd 2010
thanks Zoran, I’ll try to look at Tamarkin paper as soon as these TQFT toy models will have stopped obsessing me.. :)
I’m currently still trying to understand which vector space is associated to a 2-manifold by the DW model..
at the moment the idea I’m pursuing is something like the following: the background field is a map . if is a 3-manifold, transgressing gives a map and the target space is non-connected (in general). so its first interesting topological invariant is .
when is 2-dimensional, instead, is 1-connected, but (I guess) not 2-connected. Let be universal cover of and let us pull this back to . we obtain a cover of the (non connected) space . now I’d like to associate a flat vector bundle to this cover. to do this, recall that is a principal -bundle over , so the only thing I need is a representation of .
I’m unfortunately been unable so far to compute this fundamental group, which however I guess should be closely related to : the idea is that a path in is an element in , and is now a 3-manifold (with boundary..), and for a (closed connected) 3-manifold one has .
should this relation between and come true, then we would have the defining representation of and would end up with a flat line bundle on . the space of its flat section would then be the vector space associated to .
-
- CommentRowNumber116.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 22nd 2010
quite unbelievable, but what I was conjecturing about for a closed connected surface was correct! :)
here is a reference: Spaces of maps into Eilenberg MacLane spaces, Vagn Lundsgaard Hansen, Can. J. Math., XXXIII n.4 (1981), 782-785 (one finds it on google books, but I’ve been unable to link to that). I think it’s worth adding Thom-Federer and Gottlieb theorems (Theorems 1 and 2 in the reference) and to Eilenberg-Mac Lane space. I’ll do this tomorrow; too tired for doing it now.
-
- CommentRowNumber117.
- CommentAuthorzskoda
- CommentTimeApr 22nd 2010
Federer of the geometric measure theory ? I do not know what is Thom-Federer theorem...but have hi opinion of Federer.
-
- CommentRowNumber118.
- CommentAuthorUrs
- CommentTimeApr 22nd 2010
Thanks, Domenico! That’s very useful. I am on a bad internet connection, so I gave trouble checking google boks at the moment. What’s the statement of the general theorem here?
-
- CommentRowNumber119.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
- (edited Apr 23rd 2010)
yes, that Federer :)
here are the statements from the reference:
Theorem 1: let be a discrete abelian group, and a connected CW-complex. then , for .
Theorem 2: let be any discrete group, and let be a finite dimensional connected CW-complex. For a fixed map , let be the centralizer in of . Then the connected component of in is a 1-type, with .
-
- CommentRowNumber120.
- CommentAuthorUrs
- CommentTimeApr 23rd 2010
Thanks, Domenico.
That theorem 1 I consider a general triviality. Theorem 2 is useful. But how does this imply statements like for general closed ?
-
- CommentRowNumber121.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
- (edited Apr 23rd 2010)
Yes, Theorem 1 is almost trivial: it is completely trivial in case is connected, and with little effort one works on a connected component in the nonconnected case.
let me sketch the proof of the trivial case for our readers: since is abelian, is an H-space, and so is with pointwise multiplication. hence acts trivially on , and so this latter group is identifies with . this cohomology group will have two contributions, one from and the other from . since we are assuming is connected, .
But how does this imply statements like $\pi_0Top(M,B^3U(1))=U(1)$ for general closed M?
this I was not referring to, since I was considering the 3-manifolds/ case as acquired, and so I directly moved to 2-manifolds, where is involved. as far as concerns : what we want is for a compact closed oriented . and this is just universal coefficients plus the fact that is an injective -module: .
-
- CommentRowNumber122.
- CommentAuthorTim_Porter
- CommentTimeApr 23rd 2010
This reminds me of some of the results in my paper with Joao ( J. Faria Martins and T.P., On Yetter's Invariant and an Extension of the Dijkgraaf-Witten Invariant to Categorical Groups, Theory and Applications of Categories,18, 2007, No. 4, pp 118-150; (available also at ArXiv: math.QA/0608484) and perhaps it is worth glancing at the calculations we did there.
-
- CommentRowNumber123.
- CommentAuthorUrs
- CommentTimeApr 23rd 2010
- (edited Apr 23rd 2010)
Domenico,
I was thinking about theorem 1 that this works in full generality, for any two objects
 and
and  in an oo-topos we have
in an oo-topos we have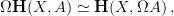
because forming loop space objects is taking homs and limits, and both are respected by
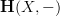 .
.So it follows generally that
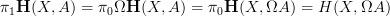 .
.Concerning the second theorem
this is just universal coefficients plus the fact that
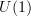 is an injective
is an injective  -module:
-module:Ah, thanks, I have an education gap here. Need to remind myself of the universal coefficient theorem...
-
- CommentRowNumber124.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
- (edited Apr 23rd 2010)
Tim,
thanks for the reference!
Urs,
your proof of Theorem 1 in a oo-topos is extremely nice! and we finally have boldface in markdown-itex: :)
As far as concerns the universal coefficients theorem, it states one has a short exact sequence of abelian groups
If the abelian group is injective as a -module, then for .
-
- CommentRowNumber125.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
let me sum up what we have so far for the vector space the DW-model should associate with a closed connected 2-manifold : over the space there is a canonical principal -bundle. since we are considering as a discrete goup, this is automatically flat, and so the defining representation of induces a flat -bundle over . pulling this bak via the background field, one has a flat line bundle over . taking flat sections, i.e. pushing forward to a point, we obtain the vector space .
next steps are describing the linear operator associated with a cospan , and describing the additive category the (extended) DW-model associates wit . a clear indication of what the latter should be is in the preprint by Urs and Zoran, so I’ll concentrate on this now.
(and I have to add Theorems 1 & 2 of post 119 to Eilenberg-MacLane space, will do during the weekend)
-
- CommentRowNumber126.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
mmm.. the pattern just used for 2-manifolds seems to continue to 1-manifolds.. the space is connected and simply connected, so can look at its 2-connected cover, which is a -bundle over . but we have just said that , so we have a canonical (2-flat? that is what should be) -bundle over and by the background field we can pull this back to a 2-flat (?) -bundle over . now, I’d like to have a sort of “defining representation” of to end up with a 2-flat linear 2-bundle over , whose 2-flat sections could be the desired linear category.
any suggestion? :)
-
- CommentRowNumber127.
- CommentAuthorUrs
- CommentTimeApr 23rd 2010
- (edited Apr 23rd 2010)
Domenico,
it looks like you are onto something here.
I’d like to have a sort of “defining representation” of to end up with a 2-flat linear 2-bundle over , whose 2-flat sections could be the desired linear category.
any suggestion? :)
Yes:
a 2-vector space is a category of modules over some algebra (or algebroid, more generally).
Every strict 2-group coming from a crossed module has a canonical 2-reprepresentation induced from any ordinary representation of :
the representation sends
the single object to – the algebra generated from the linear operators in the image of ;
a 1-morphism to the -bimodule which is itself as a vector space, with the obvious acton from the left and the -twisted action from the right, where we use thatfrom the crossed module has a homomorphism to which in turn acts on by algebra automorphisms (by its action on the generators).
a 2-morphism to the bimodule homomorphism obtained from multiplying with from the right.
For the simple case of and the standard representation of on , this induces a canonical 2-representation of :
the representation 2-vector space is the one induced by the algebra , hence is ;
the single 1-morphism goes to the identity bimodule, = the identity functr ;
the 2-morphism goes to the -bimodule homomorphism given by multiplying with , i.e. the natural transformation of the identityfunctor on given in components by multiplication by .
-
- CommentRowNumber128.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 23rd 2010
mmm.. this calls for the final step: down to the point. in this case we should just be looking to the 3-connected cover of ; this shold be a 3-flat -bundle, and as such should induce a standard 3-flat 3-vector bundle on which we can pull back to via the background field. taking 3-flat sections could then produce the seeked .
-
- CommentRowNumber129.
- CommentAuthorUrs
- CommentTimeApr 23rd 2010
Right, I think we mentioned this before somewhere.
A 3-vector-space is given by an weak algebra object in , i.e. . And so on. See the end of Topological Quantum Field Theories from Compact Lie Groups for an indication of te full story.
Again in the very simple case of there is a canonical 3-representation which
sends the point to regarded as a trivial algebra object structure on the algebra
sends the single morphism of to regarded as the identity bimodule object in on ;
sends the single 2-morphism of to regarded as the bimodule homomorphsim object in on ;
sends the 3-morphism of to the evident (once one thinks about it) multiplication operation. :-)
-
- CommentRowNumber130.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 24th 2010
Yes! I now see we are precisely in the situation described in the box at the end of Topological Quantum Field Theories from Compact Lie Groups. somehow I had to redo the whole way by myself to understant it, but I’m here now :)
so we start with a background field and we end up with a canonical morphism
and we want to obtain an extended 3-dimensional TQFT out of this, pushing forward along .
-
- CommentRowNumber131.
- CommentAuthorUrs
- CommentTimeApr 24th 2010
Yes! Only that we still need a better idea of what “pushing” means here exactly.
Maybe we can join forces on this: I mean to write an nLab entry on the standard theory of push-forward in Eilenberg-Steenrod generalized cohomology. You know, the procedure where you form normal bundles and Thom spaces, choose a spectrum-orientation etc. We should have a close look at this and extract the functorial abstract nonsense that hopefully underlies it.
-
- CommentRowNumber132.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 24th 2010
I’m in the game :)
I was going to say we should start a new discussion on push-forwards in cohomology, since I suspect this could to be of interest to a wider audience than generalized TQFTs, but I see you’ve already done :)
-
- CommentRowNumber133.
- CommentAuthorUrs
- CommentTimeApr 24th 2010
Yes. In case sombody hasn’t noticed it yet: I started fiber integration.
-
- CommentRowNumber134.
- CommentAuthorzskoda
- CommentTimeApr 25th 2010
129 Is this picture on 3-Vect in TFT fundamentally different of the picture in CFT context where Douglas et al. form a 3-category of conformal nets to feed into the Stolz-Teichner picture. I mean something as fundamental as elliptic cohomology should in first approximation come from something as simple as working the way we do here; on the other hand, the 3cat of conformal nets took few years to construct, not to mention now to use. Finally why Segal in the first place suggested that the loop space picture (and thus by the transgression the relation to the appropriate K theory of 2-bundles) is not sophisticated enough but one needs full fledged conformal field theory kind of picture ?
-
- CommentRowNumber135.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 26th 2010
Zoran,
indeed the emergin picture for DW seems to be extremely neat and simple, maybe too simple..
as a convincing test I’m trying to see how the Drinfeld double modular tensor category from DW you describe in your paper with Urs is expressed in the topological formulation I’ve sketched above for DW, assuming we have good notions of pushforwards in cohomology wherever needed
-
- CommentRowNumber136.
- CommentAuthorzskoda
- CommentTimeApr 26th 2010
There is a nice approach of Paul Bressler from 2002 on Pasquier-Rocher-Dijkgraaf-Witten model where he actually emphasised the role of loop space of loop space. Namely the SL(2,Z)-action which is responsible for modularity of CFT is coming from this second iteration, the fact that one has TWO transgression is responsible for 2 in SL(2,Z); one can imagine models with SL(n,Z) in the game and higher transgressions in the game. Then the formulas become really complicated. Bressler says that all these things were known much befroe his work so he never wanted to publish his manuscript (I have excerpts from ms and I was in some of his talks…). There is much about relation to cyclic picture and inertia orbifolds. This enabled me to conjecture in 2002, and prove independently in 2004, what is now called Hinich’s theorem (Drinfeld double of orbifold, arxiv) later used in BenZvi-Nadler; and also to suspect the role of monads in the business of Connes-Moscovici Hopf algebra cyclic homology with coefficients (my preprint on cyclic objects from comonads was the first attempt to see the role of Yang-Baxter in cyclic homology via comonads, and then Bohm-Stefan found independently more complete result which had my case as a special case and also the Connes-Moscovici as another special case).
-
- CommentRowNumber137.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 27th 2010
I’m now dealing with the notion of section as is in Urs and Zoran’s 1004.2472v1. this is closely related with a right Kan extension, as follows.
let a pointed oo-category (nice, i.e., with all the properties needed in what follows) and another nice oo-category. finally, let be a functor (the geometric picture to have in mind is that is a space and an (higher) vector bundle on that space). then sections of are defined in 1004.2472v1 as , where is the terminal morphism. assume now has a right Kan extension along . then the universal property of Kan extension would say that . this suggests that if has internal hom’s, then a canonical choice for would be an object corepresenting the identity of , so that in this case.
this gives for instance the choice in case is the category of -vector spaces, as in 1004.2472v1 9.1.
-
- CommentRowNumber138.
- CommentAuthorUrs
- CommentTimeApr 27th 2010
- (edited Apr 27th 2010)
Domenico,
thnaks, yes.
Quick remark before I have to dash off:
I have been thinking about the following, which should be relevant: one cool model for is the symmetric monoidal (infinity,1)-category of presentable (infinity,1)-categories: the objects are all localizations of presheaf categories, the morphisms are colimit preserving oo-functors. You think of a site as a basis, the oo-presheaves on it or a reflecttive subcategory thereof as the vector space spanned by that basis, of colimits as sums and colimit preserving oo-functors as sum-preserving i.e. linear maps. This view on is that underlying much of the geometric infinity-function theory, really.
So one might want to universaly take . That would have the possibly noteworthy consequence that any “oo-vector bundle” then necessarily embeds into an -category bundle . For that lots of abstract machinery exists. For instance we know that the (infinity,1)-Grothendieck construction constructs for us the corresponding “lax pullback of the point”, i.e. the “total space” of that beast.
But most importantly maybe, there are special simple formulas for limits and colimits of oo-functors with values in or (some remarks and references are here): they are expressed as being equal to that total space or, respectively, to be the oo-category of sections of that total space.
I keep thinking that this ought to allow us to make some grand statements. But I am not quite sure that have fully obtained these ;-)
-
- CommentRowNumber139.
- CommentAuthorzskoda
- CommentTimeApr 27th 2010
- (edited Apr 27th 2010)
Do we have some page treating (internal) action -groupoids ? I mean actions of Kan complexes in terms of the associated “action Kan complex”, and its internal counterpart in some cartesian category instead of Sets ?
-
- CommentRowNumber140.
- CommentAuthorDavidRoberts
- CommentTimeApr 27th 2010
HI Zoran,
do you mean the work of Glenn (and Duskin)? If so, I don’t think we do. There’s a mention of them on the page principal 2-bundle, but the links there are not to the oo-category versions.
-
- CommentRowNumber141.
- CommentAuthorzskoda
- CommentTimeApr 27th 2010
What I meant is that the picture with abstract infinity-categorical pullbacks like in entry action groupoid should be compared with the hands on Kan complex definition like in Glenn-Duskin. If we are say in a Barr-exact category is it clear that the Glenn-Duskin construction gives the same what the infinite pullbacks like in 1-categorical version explained action groupoid gives the same. I would like to have that clear to see if I can generalize my 2006 theorem on equivariant 2-descent along internal 2-torsors in the base 2-category of fibered 2-category in the sense of Herminda, but which is a 2-stack, to infinity case in a clean way. First of all, I do not see clearly the equivariant fiber of a categorical fibration over an object acted upon by internal Kan complex in a base quasicategory.
-
- CommentRowNumber142.
- CommentAuthorUrs
- CommentTimeApr 27th 2010
the theory of action oo-groupoids beautifully parallels the 1-categorical theory: I added a remark on this at action oo-groupoid
-
- CommentRowNumber143.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 27th 2010
- (edited Apr 27th 2010)
in the meanwhile I’ve completed working out the details of representations of twisted Drinfeld doubles out of the topologicla description in #126. I’ll post it tomorrow since now I’m completely worn out and there’s the IRC seminar starting in half an hour.
a technical question to be sure (I guess the answers to both questions are yes): morphisms between 2-vector spaces are functors between categories of modules. are they required to be additive? are they required to be the tensor product with a bimodule?
-
- CommentRowNumber144.
- CommentAuthorUrs
- CommentTimeApr 27th 2010
yes, yes.
-
- CommentRowNumber145.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 28th 2010
- (edited Apr 28th 2010)
so, let me sketch a derivation of representations of twisted Drinfeld doubles for our non combinatorially oriented reader (e.g., me :) ). the basic example to have in mind here is the following: given a flat rank complex vector bundle on a topological space , fix a point in and a linear isomorphism . then these data naturally give a reresentation .
what we’re going to describe is a one-step-higher version of this. so, let be the flat 2-vector bundle on described in posts #126 and #127 above. the fiber over a point in is a 2-vector space isomorphic to . since the bundle is 2-flat, it carries a representation of . more explicitly, for every point in we have a 2-vector space , for any path an additive functor , and for every 2-simplex with edges and a natural transformation between and .
then, a section of will consist in a morphism of representations of from the trivial -bundle to . that is, for any 2-simplex in , we have a prism compatibility equation (this is the analogue in 2 dimensions of the square compatibility equation defining natural transformations of functors between 1-categories, where any 1-simplex in the source category gives rise to a square in the target category).
to be more explicit, let us denote by the three vertices of the 2-simplex, by and the three paths, and by the 2-simplex. then:
1) on the three vertices in the “top” base of the prism we have three copies of ;
2) on the three vertices in the “bottom” base of the prism we have , and ;
3) on the three “vertical” edges of the prism we have additive functors and similarly for and (since is additively generated by , one can think of as the datum of an object in , and similarly for and ).
4) on three edges of the top base we have the identity functor
5) on the three edges of the bottom base we have functors , and
6) on the top 2-simplex we have the identity natural transformation
7) on the bottom 2-simplex we have the natural transformation between and
8) on the square corresponding to the edge in the original 2-simplex we have a natural transformation ; similarly for the other two square faces of the prism.
everything in sight has to commute, and this gives the compatibility equations.
If we now take and fix an isomorphism between and , then these data correspond to:
3’) a -vector space
5’) -vector spaces , and
7’) an isomorphism
8’) isomorphisms , and such that the diagram
commutes.
-
- CommentRowNumber146.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Yes, exactly, that’s what’s going on. This prism is drawn in my article with Zoran, in the section on “twisted vector bundles”. Precisely.
There it is labeled in . Use the inclusion to get your labeling here.
Incidentally, and I have to smile a bit while typing this, precisely this reasoning appeared in November 2006 in the blog entry Flat Sections and Twisted Groupoid Reps.
The reason I have to smile is that, once again, I never got much reaction on that (as you can see there). So it’s really very enjoyable for me to talk with you about that!
-
- CommentRowNumber147.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 28th 2010
of course the prism is in your paper with Zoran: I’ve it open on the window next to this :) as I said at some point, the only thing I’m doing here is rewriting parts of your paper with Zoran for the non combinatorially-oriented reader (i.e., for myself :) ). well, to be more honest to myself, the way I’m working these days is starting with basic elements (e.g., a flat 2-vector bundle here) and trying to work out with them the most natural possile constructions, keeping as a reference point some diagram I can see in your paper. so I can figure myself as a tourist in an unknown city, with a map I do not fully understand the language. at times I say things like “mmm.. I should meet this strange prism here in the neighborhoods..” :)
and now, to the blog! I’m sure I’ll find other pieces of the map there!
-
- CommentRowNumber148.
- CommentAuthorUrs
- CommentTimeApr 28th 2010
Okay, great. Thanks Domenico. I am hoping at some point we copy-and-paste some of the comments here into Dijkgraaf-Witten theory.
-
- CommentRowNumber149.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 28th 2010
sure. but before moving to the nLab, I’d like to work out something here on the nForum on morphism in DW theory. I mean, now we have a quite simple and uniform understanding of the “spaces” associated with closed manifolds in terms of sections of flat bundles. this is half of the Freed-Hopkins-Lurie-Teleman picture, so we should now be able to work out the other half: morphisms associated with manifolds with boundary. for instance, spheres with three holes should induce the fusion product of representations of twisted Drinfeld doubles. so I’ve now to study the fusion of bibranes from your paper :)
-
- CommentRowNumber150.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
so, let us work out trivial bibranes today. for each positive integer , let be the set . for every such , we can look at as to a (trivial) rank 1 -vector bundle over . now consider the span of sets , where the two arrows are the two projections and . then on the set we have two line bundles: and . the set of -bibranes over is the set of morphisms of vector bundles . note that, since both and are trivial line bundles over , any such a morphism is a map , i.e., a set of elements of with two indices ranging between and and and respectively. ok, now you already see the conclusion, so I could stop here, but let me write it just for the sake of writing…
associating to correspond to considering the functor which maps each object to (here we are considering as a trivial category), and the set of -bibranes over is nothing but the set of natural transformations between and .
assume now an -bibrane and an -bibrane are given. then we have the following diagram of functors with natural transformations
which we can complete to
the outside square herecomes equipped with a natural transformation between the composition of the left edges and the composition of the right edges; but it is not an -bibrane over , since the top vertex is not . however, there’s a natural map , and we can push the whole diagram along this map to get an -bibrane over . the natural transformation will be a collection of elements of , and since is given by a push-forward, these will be given by integration along the fibres of . explicitly
that is (let’s be completely explicit! :) )
so we’ve found what we all knew: matrix multiplication makes no sense except in the light of higher category theory :P
(to be continued with action of bibranes on branes, but have to go now: zbl bounty hunters are on my tracks..)
-
- CommentRowNumber151.
- CommentAuthorUrs
- CommentTimeApr 29th 2010
Hi Domenico,
nice, thanks. You know, you really should fill all this into some nLab entry, where suitable. Please do.
Something along these lines is for instance at category algebra.
I wish I had time for this now, but i am absorbed with reflective oo-subcategories for the time being…
-
- CommentRowNumber152.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
Urs,
don’t worry: everything in this thread will be cleaned up and transferred in the nLab, just give me the time to arrive to some conclusion here and there :)
I was now thinking on bibranes and their action on barnes as it is defined in your paper with Zoran. you begin with bibranes with “arbitrary top vertex”, and in this context you have a natural fucion product: from a -bibrane (i.e. a bibrane with on top) and a -bibrane you naturally get a -bibrane. this works very nicely and is very generat, but as the matrix product example shows, this is not what one usually wants. so you choose a monad ; this way from two -branes you get a -brane and pushing this forward along you get a -brane again. and this too is extremely nice. finally you say that branes are bibranes of a particular type, and so there’s a natural action of bibranes on branes. and I agree, but I think it should be said better:
1) if we use arbitrary ’s, then the fusion of a -bibrane with a -brane is a -brane, and we may be happy with this, but it is often not what we had in mind (again, the matrix action on vectors example)
2) if we use a monad , then the fusion of a -bibrane with a -brane is a -brane, but this is way too restrictive (e.g. the charged quantum particle example does not nicely fit within this pattern (it can be made to fit, but I feel this is forced))
what I would propse is something lying in between 1) and 2): a monoid and a -module , i.e., an object with a morphism with the axioms of module satisfied. in this setting we would have a natural action of -bibranes on -branes, and this seems to be a convenient framework to work with. what do you think?
-
- CommentRowNumber153.
- CommentAuthorUrs
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
Yes, right we can do this. Effectively there is the bicategory of spans, and one can consider monoids in it and modules over these monoids. Here the spans are enhanced to “bibranes” and again we can look for monoids and for modules over thes monoids, yes. (This bibrane category is what Lurie calls the “Fam”-category in his TFT-classification article.)
The modules can be related to boundary conditons. For instance the bibrane that gives the fusion product for the DW model is really to be understood as arising from homming the “string cospan” into the target space to get , and the monoid structure and hence then the fusion product is obtained from the “string concatenation product”. For what you are suggesting one would have a situation where this string would sit with one end on something, and we would get an action instead of just a product. Yes. I would have to think more about this, in this direction, though.
-
- CommentRowNumber154.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
yes. let us work out the charged particle example.
here the geometric datum is a manifold endowed with avector bundle with a connection . our monad is the space of paths from to , or, more precisely, the span . the monad structure is given by composition of paths (this is associative up to thin homotopy). our module is the span . the action of the monad on the module is , where is a point in and is a path in with .
now look at branes and bibranes. considering the vector bundle as a functor (the source category is , we are not considering the connection here) branes
are sections of . holonomy of the connection along path in is a morphis of bundles over , namely, it is a morphism of bundles between and . so it is a bibrane
fusion then produces a brane
and pushing this forward along we finally obtain an -brane, i.e., a section of . this way bibrane action maps a section of to another section of . if we want to see more explicitly which is the section obrained from a section , we have to work out the push-forward. this is given by fiber-integration along , so the value of at a point in is given by
:)
-
- CommentRowNumber155.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 29th 2010
so, in general it seems all we need is a pushforward. more precisely, if we adopt the “ is a -module” formalism, what we need is a pushforward between -branes and -branes induced by the module structure morphism . in full generality it’s not clear to me whether we have such a pushforward, and under which hypothesis. yet, in finite models (e.g. the DW model) we should be able to work it out.
-
- CommentRowNumber156.
- CommentAuthorUrs
- CommentTimeApr 29th 2010
- (edited Apr 29th 2010)
Right, that push-forward of bibranes still needs being formulated abstractly, so that it happens “by itself” and doesn’t need us to do it by hand-
I think for that one needs to categorify a bit and replace numbers by (tame) -groupoids. An -groupoid corresponds to the number , if that exists.
So replace with (the symmetric monoidal (infinity,1)-category of presentable (infinity,1)-categories). In there itself plays the role of the ground field regarded as a vector space over itself. Consider in the following hence a “line bundle” that assigns to every point.
The linear maps are colimit preserving functors. Since every object in is an -colimit of copies of the point, such a linear functor is determined by what it does to the unit , hence is entirely determined by an -groupoid itself.
This is entirely analogous to how a linear map is fixed by its value on the unit 1 as
This categorification of numbers to -groupoids is necessary in order to get the follwong to work: given two bibranes
and
we want a category of morphism betwen them, so that we can do Kan extension of bi-branes to describe push-forward, something we can’t do if instead of we use .
So if we take for simplicity to be the trivial line bundle, i.e. the functor constant on the object then the components of and will be ovber each point a linear map
and
But these now have transformations between them
Think about the naturality condition for these transformations: over a morphism in the component is
I have to think about if it is really the general case, but at least once class of solutions of this comes from taking a fixed -functor and setting .
With that in hand now consider the functor from the category of bibranes of the form
to that of bibranes of the form
given by precomposition at the tip with .
Then form the right adjoint of that functor. That should be the push-forward in question (after decategorification of the respective component -groupoids). By the fact that we have morphisms between our numbers, that Kan extension should just form the coproduct of -groupoids etc, hence just sum up the corresponding -groupoid cardinalities. As it should.
I am getting a bit too tired to do this justice now.
-
- CommentRowNumber157.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 30th 2010
- (edited Apr 30th 2010)
precomposition at the tip with $s:P_1(X) \to X$$.
I’m ot sure about this: the charged paticle example in #154 above seems to suggest that the push-forward should be along rather than along .
I agree we have to categorify to get a nice pushforward.
-
- CommentRowNumber158.
- CommentAuthorUrs
- CommentTimeApr 30th 2010
But is just .
-
- CommentRowNumber159.
- CommentAuthorUrs
- CommentTimeApr 30th 2010
On the other hand, elsewhere we said that the right internal analog of , i.e. when we pass to the parameterized sitution (smooth, notably) and want the stack of vector bundles, should be: take an oo-site such as the duals of simplicial smooth algebras , , and then let be the stack classifying its tangent -category fibration.
It would be interesting to play the bi-brane game in this context, with replaced by this way. But I am afraid that the special mechanism that I used above with as a model for won’t work, since this , while certainly a higher categorical version of , does not come with “categorified numbers”.
It’s all still a bit confusing. :-)
-
- CommentRowNumber160.
- CommentAuthorEric
- CommentTimeApr 30th 2010
But is just .
On an otherwise extremely stressful day, this put a smile on my face for some reason :)
-
- CommentRowNumber161.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 30th 2010
- (edited Apr 30th 2010)
But is just .
sure, I was enjoying so much the general picture that I missed what it becomes in this particular case :(
coming back to the general problem, I agree with the approach in #156: at the level of objects the morphism induces a map between -branes and -branes. so we would like to have a category of bibranes so that is a functor. and we would like to have an adjoint . this would be the pushforward. yes, it could work like this.
-
- CommentRowNumber162.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 30th 2010
I’ve worked aout a very simple geometric example whcih could help us seeing which is the rght thing to ask.
consider a morphism of manifolds and two vector bundles amd over . finally, let be a morphism of bundles over . for any , let be the fibre of over . these are our data. then, for every , the morphis gives a morphism , i.e. an element of the vector space . therefore, if comes equipped with a measure, we can integrate on the fibre and get a morphism . the collection of these gives a morphism of bundles over , .
this is very naive, but maybe clarifies an aspect: an integration measure on fibres is needed, and this is independent of all other data. in the oo-groupoid version of this groupoid cardinality seems to provide the correct integration measure (we’ve already said this, but repeating at times can be useful, one has thought other things in the meanwhile..)
-
- CommentRowNumber163.
- CommentAuthorUrs
- CommentTimeApr 30th 2010
an integration measure on fibres is needed, and this is independent of all other data. in the oo-groupoid version of this groupoid cardinality seems to provide the correct integration measure (we’ve already said this, but repeating at times can be useful, one has thought other things in the meanwhile..)
Yes, right, explicitly or not, there is a measure in the game. Of course in the path integral that we want to see, that is the most delicate ingredient. For the finite cases it is just the counting measure corrected by “gauge invariance”, a kind of discrete BRST measure, and that turns out to be nothing but the groupoid cardinality measure. Yes.
At some point I had been hoping that the groupoid or more generally the category measure would serve for all purposes, in some limit. In that we think for instance of a manifold as a continuum limit of some graph, which we think of as some category, which we have a canonical measure for. But I am not sure if that can be made to work in a fully satisfactory way.
In this context I was wondering if it is noteworthy that a Lorentzian manifold is really just a smooth posetal category with a volume measure on it. That may be relevant here. Or maybe not. It’s really a subtle issue Which is why I am more than glad that I can talk about this with you.
This gets to Sorkin’s old idea: he said effectively that if a Lorentzian manifold is just a poset with a measure on it, then clearly this indicates that fundamentally it should really just be a “coarse grained” poset, namely where we take just the counting measure on its objects but have the “density” of objects vary, such as to give a varying effective measure.
If something like that is assumed, then we can get away with using just bare categories (groupoids, higher groupoids) as we did, with their intrinsic cardinality. This would seem conceptually very satisfactory, if it works out all right. But one will still have to see how it really does work out.
-
- CommentRowNumber164.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 1st 2010
- (edited May 1st 2010)
Yes, right, explicitly or not, there is a measure in the game. Of course in the path integral that we want to see, that is the most delicate ingredient. For the finite cases it is just the counting measure corrected by “gauge invariance”, a kind of discrete BRST measure, and that turns out to be nothing but the groupoid cardinality measure. Yes.
Indeed, the oo-groupoid measure precisely does (and in a single step!) what BRST-type measures are supposed to do: one looks at isomorphism classes of objects (and this is as taking a gauge-fixing slice of representing field configurations in the BRST gauge-fixing); each object is weighted by its automorphism group (ghosts in the BRST parlance); and then further weighted by automorphisms of automorpisms (ghosts of ghosts), and so on.
in the discrete case, the counting measure is taken at each step. in the general case we should expect something involving measures on all homotopy groups.
-
- CommentRowNumber165.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 1st 2010
looking back through this entry, I feel we have a consistent amount of material on the DW model so far. so I think it’s time stopping posting here for a while and starting cleaning up and copying and pasting into the lab. I’ll do during the whole next week. (Urs must be not believing in what he’s reading.. :) )
-
- CommentRowNumber166.
- CommentAuthorUrs
- CommentTimeMay 2nd 2010
- (edited May 2nd 2010)
Indeed, the oo-groupoid measure precisely does (and in a single step!) what BRST-type measures are supposed to do:
Yes, indeed. Moreover, one can notice that the BRST complex is nothing but the Chevalley-Eilenberg algebra of the Lie n-algebroid corresponding to the action n-groupoid of the gauge n-group acting on the space of fields.
-
- CommentRowNumber167.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 3rd 2010
- (edited May 3rd 2010)
I’m now working on the following toy example: a 1-dimensional TQFT out of a finite rank flat vector bundle on with a finite group. In order to forget orientability issues, assume further an equivariant inner product on is defined: given two vectors and in the fibre and a path , one has . A pairing is then defined for any path as .
The vector space associated to a point by the TQFT arising from these data is the space of flat sections of . The inner product on is
The operator associated with the 1-manifold is
The complex number associated to the 1-manifold is
there are several checks to be made: is finite dimensional? is the identity operator? is the dimension of ? I’ll do them in the next post.
-
- CommentRowNumber168.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 3rd 2010
- (edited May 3rd 2010)
1) is finite dimensional? sure: fix a point in , and let be the fibre of at . the holonomy action of gives a representation of on . evaluation at , induces an isomorphims between and , the subspace of -invariant elements of . since is finite dimensional, so is .
2) is the identity operator? this is trivial: since is a flat section, for any . so the forula for reduces to
and the only thing we need to check is that . which is the measure we have on this space of paths? the Leinster measure prescription tells us that integartion on the groupoid (with fixed and ) is the sum over with the point weighted by . Since the space is a 1-type, this weight is 1, and integration over produces a factor . similarly, integration over is the sum over a single point (the space is connected) weighted by the weight . In the end , as we wanted.
3) is the dimension of ? of course: since is connected, is identified with the quotient of by the adjoint action on itself. in other words, the groupoid (the free loop speace on ) we are integrating on is equivalent to the action groupoid . so we have a point for every element of , and each point is weighted by the weight . the trace of the holonomy of can be computed fixing an arbitrary basepoint, so we can chose as basepoint; what we are then computing are the traces of the operators , where is an element of and is the holonomy representation of on . we therefore find
now open your favourite book on representations of finite groups…
-
- CommentRowNumber169.
- CommentAuthorUrs
- CommentTimeMay 3rd 2010
I’m now working on the following toy example: a 1-dimensional TQFT out of a finite rank flat vector bundle on with a finite group.
All right, very good. For comparison, notice that this is discussed briefly also on p. 4 of FHLT.
A complex vector bundle on is classified by which is – an group character.
is finite dimensional? sure:
Yes, I guess you can shortcut your argument a little by explicitly fixing the model for from the beginning. The vector bundle associated to our clssifying map is just the action groupoid of the vector space on which represents by this induced action of , and the projection map just forgets all the vectors and just remembers the -action.
I would have thought that what I just said is what you are thinking about anyway, but now I am not so sure. What are those paths that you consider under point 2), precisely?
-
- CommentRowNumber170.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 3rd 2010
Yes, I guess you can shortcut your argument a little by explicitly fixing the model for from the beginning
I agree. but I wrote that topologically in an attemp to bridge the “categorical divide” a potential reader could have.
A complex vector bundle on is classified by
I would say this for line bundles rathere than vector bundles, which should be classified by . but I agree line bundles are the relevant example in the DW direction.
What are those paths that you consider under point 2), precisely?
I had in mind paths for a variable point to a fixed point . one splits the integration into a two-steps integration: one over and one over paths from to with both endpoints fixed.
-
- CommentRowNumber171.
- CommentAuthorUrs
- CommentTimeMay 3rd 2010
I would say this for line bundles rathere than vector bundles,
Right, sure.
I had in mind paths for a variable point x to a fixed point y.
Okay, but what is a path here? A continuous map from the interval to the topological space ?
I think we should look at this in the finite groupoid model, there it is simpler.
-
- CommentRowNumber172.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 3rd 2010
Okay, but what is a path here? A continuous map from the interval to the topological space ?
yes. the idea is that since the connection is flat, all paths in the same homotopy class give the same contribution, so there is an “infinite factor” that “gauge fixing” takes automatically care of, reducing to the finite groupoid model.
-
- CommentRowNumber173.
- CommentAuthorUrs
- CommentTimeMay 3rd 2010
I see, okay. I was just thinking that it might be more helpful to stick to the finite models, using more of the abstract nonsense, but possibly you are right that it helps readers to lift essentially trivial entities here to huge ill-defined sums quotiented by huge ill-defined gauge fixing terms. That may make it look more familiar. ;-)
-
- CommentRowNumber174.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 4th 2010
- (edited May 4th 2010)
That may make it look more familiar. ;-)
yes, that’s precisely my intent. I think we can use DW model to bring the reader back and forth between a familiar ill defined sigma model picture and a maybe less familiar but completely rigorous finite groupoid picture. it could be a nice palying field for an invitation to higher categories in everyday maths. I’d like to write a note on this, but later: first, as promised, I’ll move cleaned up contents from this discussion into the Lab.
just a little (but nice :-) ) addition to the proof of point 3) in #168. we can compute the integral
also directly using the Leistner measure on , without realizing it as . namely, is the set of conjugacy classes of and, as noticed in #119, if is a representative of the conjugacy class of , then the connected component of in is a 1-type, with fundamental group , the centralizer of in . therefore
now reopen your favorite book on representation theory (or work it out yourself, which is faster.. :-) )
-
- CommentRowNumber175.
- CommentAuthorUrs
- CommentTimeMay 4th 2010
Hi Domenico,
yes, right, I agree.
By the way, these computations as you spell out here can be found discussed in some detail in Simon Willerton’s article.
-
- CommentRowNumber176.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 4th 2010
By the way, these computations as you spell out here can be found discussed in some detail in Simon Willerton’s article.
I see, and I should have seen before, everything I’ve been writing lately is already there. and also the background field with values in and in , I was going to write as simpler cases of the DW model are already there. a bit depresssed, now :-(
ok, I’ll think to something else. and I’ll still mantain my promise of writing a clean DW model entry on the nLab :-)
-
- CommentRowNumber177.
- CommentAuthorEric
- CommentTimeMay 4th 2010
a bit depresssed, now :-(
When I rediscover something, I’m usual happy. It means I was on the right track :)
The more recent the rediscovery, the better. I used to rediscover results that were 100+ years old and as I progressed, I’d rediscover new and newer things. Simon’s article is just 5 years old. I have no doubt there will be new insights coming out of this discussion :)
-
- CommentRowNumber178.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 4th 2010
Thanks, Eric :-)
actually I don’t feel that bad, but in the last few days I had really been thinking writing a short note on the DW model could have been a nice idea. now I see it’s not worth doing.
yet, on second thought, I have a vague impression in Simon Willerton’s paper only 0-1-2-3 manifolds without boundary are discussed. from a very abstract perspective this is more than enough: via the cobordims hypothesis, only the linear 2-category associated with the point counts, and all the rest follows from this. after all, according to the nLab entry on Topological Quantum Field Theories from Compact Lie Groups, “what exactly the functor does to -morphisms is apparently left as an exercise for the inclined reader.”. so maybe working out that exercise for the DW model is worth doing. or maybe not?
-
- CommentRowNumber179.
- CommentAuthorEric
- CommentTimeMay 4th 2010
now I see it’s not worth doing.
Au contraire :)
I would LOVE to see a write up from you on this subject. You have a rare talent to write stuff that I can understand (sometimes!).
-
- CommentRowNumber180.
- CommentAuthorUrs
- CommentTimeMay 4th 2010
I see, and I should have seen before, everything I’ve been writing lately is already there. and also the background field with values in and in , I was going to write as simpler cases of the DW model are already there. a bit depresssed, now :-(
Domenico,
sorry for that. I would have mentioned this before, had I been actively aware that it needs mentioning. My bad.
But I do think there is something to add here, from the perspective that we have been entertaining here, namely amplifying the point that really everything in sight has nice natural expressions in terms of some general oo-groupoid machinery. This was for instance part of the motivation of that section on the Drinfeld double in my writeup with Zoran, to show that this transgressed cocycle on has a nice general-nonsense expression as an internal hom.
So while lots of the formulas are already known, I do still think a few gems are still to be picked here by putting all this in its completely right general perspective. Namely having this and then internalizing everything from the oo-topos to something like should tell us a lot about Chern-Simons theory etc.
So i think there is no need to be depressed for you, given the discussion we had here. On the contrary.
-
- CommentRowNumber181.
- CommentAuthorUrs
- CommentTimeMay 4th 2010
“what exactly the functor does to -morphisms is apparently left as an exercise for the inclined reader.” so maybe working out that exercise for the DW model is worth doing. or maybe not?
Definitely, yes. I should say that Johan Alm had thought about this hard back then when we looked into this, and some things became clear, but a general puzzlement on one point was unfortunately left.
-
- CommentRowNumber182.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 4th 2010
Urs,
no reason to be sorry. On the contrary, should I have had my attention pointed to Simon Willerton’s paper from the beginning, I would have never gone so deep in my understanding of DW. so it’s much better things have gone this way. really. I’ve had an “and now? what’s left to do? nothing!” moment, but it’s gone, now :-)
-
- CommentRowNumber183.
- CommentAuthorBruce
- CommentTimeMay 5th 2010
As far as I understand it, there still hasn’t appeared a simple geometric description of the full 1-2-3 finite group TQFT (let alone the 0-1-2-3) theory. As you say, one can write down the numbers, vector spaces, linear categories, and linear 2-categories associated to closed 3-manifolds, 2-manifolds, 1-manifolds and points respectively, and that’s nice, but often people sort of stop there because our language for dealing with the functors and the 2-morphisms etc. associated to cobordisms between cobordisms and so on seems to be unwieldy.
With the 1-2-3 version of the 3d finite group TQFT, one way to proceed is to write down the category associated to the circle. Then if someone asks you “calculate the linear map assigned to this cobordism between cobordisms”, you do a Turaev kind of construction on that category. So you let R = (+) X_i (x) X_i^*, and play games with that thing. It works, but it’s not a “first principles” solution; one would really like to be able to describe everything geometrically from first principles. Freed kind of did that in the 90’s, working out explicitly the braiding, twist, etc., but my impression was that it was still not a “first-principles” thing; there wasn’t an explicit geometric formula for working out “the natural transformation corresponding to this cobordism from this cobordism to that one”, although people can write such formulas down after making a few choices, basepoints, etc.
So in conclusion: I think there’s still lots of room here for elegant geometric explanations along the lines you have been working out, Domenico! Where one tries to be as canonical as possible.
Also, along these lines: In the 90’s people talked about “C-extended” TQFT’s, where C is some linear category. Remember, from Turaev’s book? This formalism was carried on in Bakalov and Kirillov. My understanding is that nowadays we would refer to a “C-extended TQFTs” simply as a 1-2-3 TQFT (C is the category assigned to the circle). But even this equivalence hasn’t been made entirely precise, as far as I’m aware.
-
- CommentRowNumber184.
- CommentAuthorBruce
- CommentTimeMay 5th 2010
Just after my post I realized I was talking nonsense as usual. Jeffrey Morton’s thesis, of course, does a complete and canonical geometric description of the full untwisted finite group 1-2-3 model; nice summary of the construction on the arXiv at arXiv:1003.5603. Ok, but I guess it’s the twisted case where Kantization really comes into its own..?
-
- CommentRowNumber185.
- CommentAuthorUrs
- CommentTimeMay 5th 2010
one would really like to be able to describe everything geometrically from first principles.
I am relieved to hear you say this! Hopefully you find a free minute here and there to help Domenico and me and others here think about that.
-
- CommentRowNumber186.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 5th 2010
My understanding is that nowadays we would refer to a “C-extended TQFTs” simply as a 1-2-3 TQFT
I completely agree with this. And, if I correctly understand Bruce point of view, the main puzzle here is something of this kind: assume we are given the tensor category associated with the circle; then we can compute a 3-manifold invariant by playing some suitable Turav game. On the other hand the same data we have should be the shadow of a sigma model (with some background field), and in this sigma model we would have an “obviously defined” 3-manifolds invariant, given by the path integral. So the result of the Turaev game should be thought as the result of the ill-defined path integral. But then there’s a check to be made (as in the very toy example at #167): at least in finite models we are also able to compute directly the path integral in a rigorous way. So we now have two 3-manifolds invariants which should be the same, and we have to check this, or (better) find a first principle telling us they are the same (a mathematical first principle, I mean.. I guess from a physics perspective they must obviously be the same :-) )
-
- CommentRowNumber187.
- CommentAuthorBruce
- CommentTimeMay 6th 2010
Ok, I completely agree with that summary of affairs. I don’t have anything interesting to say right now! So carry on with your computations, don’t let me sidetrack them.
-
- CommentRowNumber188.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 7th 2010
Thanks, Bruce. I’m glad you agree. I’ve been terribly busy during the last couple of days (not even able to work on the DW entry in the Lab, sorry for this), but now I’ll try to sketch a few lines of a sort of small research project along the lines above:
The state of the art of the functorial point of view on 3D TQFT during the ’90s can be summarized in this sentence from the introduction of Bakalov-Kirillov’s book: “under some (not too restrictive) assumptions, the notions of modular tensor category, 3D TQFT and 2D modular functor (topological and complex-analytic) are essentially equivalent”.
Today, we would express the first part of this quite vague “essentially equivalent” by saying that a 1-2-3 TQFT is completely determined by the modular tensor category it assigns to , and even better in terms of representations of (3-dimensional cobordism up to codimension 2). Moreover, in finite sigma models it seems we are able to give a categorical path integral construction.
Now, let us consider the complex-analytic 2D modular functor “essentially equivalent to the given 1-2-3 TQFT”. We know that the algebraic/categorical data of modular tensor category can be seen as the datum of projectively flat vector bundles on moduli spaces of complex curves. This is precisely the kind of datum we end up after path integration in string theory. So it seems that a few tricks and phenomena of string path integrals (zeta functions regularization, anomaly) are not arbitrary at all, since the result they produce is exactly of the kind one one would have computing the “categorical path integral”. And this clearly suggets that the two results should be the same.
Apparently, there are only few situations where we have both points (the categorical and the complex moduli one) of view on the path integral at the same time. this is mainly due to the difficulty of having a sigma model target which is at the same time a simple categorial object and a complex analytic object. But here comes the beauty of the DW model: if is a finite group, the target is on the categoical side the delooped groupoid , and on the complex analytic side the stack . so one should expect a Rosetta stone between the 0-1-2-3 TQFT arising from the DW model and the geometry of moduli spaces of stable maps (in particular, I would expect projectively flat vector bundles on to arise as pushforwards of flat line bundles on along the natural projection , but this is just a very vague idea).
this would provide a neat explanation for elliptic phenomena on the categorical side of the DW model (twisted elliptic characters, see Simon Willerton’s paper)
-
- CommentRowNumber189.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
Added a “As an extended TQFT” section to Dijkgraaf-Witten theory.
-
- CommentRowNumber190.
- CommentAuthorBruce
- CommentTimeMay 10th 2010
This sounds good. I am still quite a long way from understanding the complex analytic side of things; I only have a hand-waving understanding of “moduli stack”, “KZ connection” and so on, far from enough to actually do real computations with. I have spent my time in the other parts of the BK correspondence. So I am unable to contribute to the Rosetta stone at this stage. Mightn’t major parts of the Rosetta Stone already be contained in Ben-Zvi and Nadler’s geometric infinity function theory?
-
- CommentRowNumber191.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 10th 2010
Mightn’t major parts of the Rosetta Stone already be contained in Ben-Zvi and Nadler’s geometric infinity function theory?
might be.. I should look back at that having this in mind!
-
- CommentRowNumber192.
- CommentAuthorUrs
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
Added a “As an extended TQFT” section to Dijkgraaf-Witten theory.
Thanks for starting doing this, Domenico!
I have two requests:
for the equation it would be good to add a remark on how this follows from the universal coefficient theorem;
it seems to me something is missing in your discussion after that, since you describe a -vector bundle on the space of phases while you should describe one on the space of fields .
It seems to me that you really want to pull back the vector bundle that you describe along the map
I would suggest to write it like this:
By the universal coefficient theorem we find that . This means that the transgression of the background field
to the space of field configurations over is a cocycle
This classifies a -principal infinity-bundle over the space of field configurations, given by the pullback
By the canonical representation we have associated to this canonically a -vector bundle , which is the pullback
If is closed then the -vector spaces associated by the TFT to is the space of sections of this bundle .
-
- CommentRowNumber193.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 11th 2010
it seems to me something is missing in your discussion after that…
yes, absolutely! somehow I got distracted in the copy-and-past process and I forgot pulling back.. now I’ll remedy :)
-
- CommentRowNumber194.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
by the way, I feel
By the universal coefficient theorem we find that
should rather be
By the universal coefficient theorem we find that , where the subscript on the left hand side denotes the -truncation.
But I have to think more carefully to this (actually, postcomposing with the truncation morphism from a space to its -truncation, the above argument holds without changes).
-
- CommentRowNumber195.
- CommentAuthorUrs
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
Thanks, Domenico. I edited the entry a bit further, but nothing nontrivial.
You write:
by the way, I feel
By the universal coefficient theorem we find that
should rather be […]
You know, that may well be, that’s why I would like to ask you to spell out the details of your argument involving the universal coefficient theorem. I am being dense and uneducated here and would really like to understand this completely. Currently I do not. So please: spell out in full detail, for me, your argument for how to determine the homotopy type of !
-
- CommentRowNumber196.
- CommentAuthordomenico_fiorenza
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
I could be wrong, but it should be as follows: we have seen at some point that
moreover, we now (universal coefficient theorem in its classical version, but we should think to nPOV on it..) there’s an exact sequence
Since is an injective -module, and so we have an isomorphism
For , the right hand side is zero, and so for . For , instead, , since is a closed -manifold and so . After this point homotopy groups of does not seem to vanish, since has nontrivial homology in degrees .
-
- CommentRowNumber197.
- CommentAuthorUrs
- CommentTimeMay 11th 2010
Ah, thanks, that helps. Yes. I’ll put that argument into the entry…
-
- CommentRowNumber198.
- CommentAuthorUrs
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
Okay, I put in the details here in the form of a formal proposition.
Very nice, this argument that is something I had thought should be true in my discussion of “integration without integration” but didn’t really show. Very good indeed to have this. This fills a gap in my understanding of the universe. Very nice.
-
- CommentRowNumber199.
- CommentAuthorTim_Porter
- CommentTimeMay 11th 2010
@Urs There seem to be some typos in what you put in and I am not sure what exactly you intended so cannot correct them.
-
- CommentRowNumber200.
- CommentAuthorUrs
- CommentTimeMay 11th 2010
- (edited May 11th 2010)
@Urs There seem to be some typos in what you put in and I am not sure what exactly you intended so cannot correct them.
If you let me know what you think is a typo, i can try to reply.