nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: path category vs cobordisms for bundles
Bottom of Page-
- CommentRowNumber1.
- CommentAuthorDavidRoberts
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010 by Mathforge Admin)
Discussion continued from here.
Incidentally, Domenico, if we have a span (this is conjectural)
![\mathcal{P}_1(X) \leftarrow [\Delta^1,X] \to Bord_1(X) \mathcal{P}_1(X) \leftarrow [\Delta^1,X] \to Bord_1(X)](/extensions/vLaTeX/cache/latex_bd5990964eb84d8737d88577e1491067.png) where the left leg is the localisation at all arrows and the right arrow is the canonical one to the free symmetric monoidal category, then this is very cool, since the universal property of the localisation means we can go from functors
where the left leg is the localisation at all arrows and the right arrow is the canonical one to the free symmetric monoidal category, then this is very cool, since the universal property of the localisation means we can go from functors 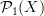 to functors
to functors 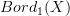 without too much trouble. All this needs checking, but puts our remarks on the other thread on a more solid footing.
without too much trouble. All this needs checking, but puts our remarks on the other thread on a more solid footing. -
- CommentRowNumber2.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010)
fine. so we can state our current problem as follows: let ; then we have a natural functor . since the target is a groupoid, this factors through a morphism , and we are wondering whether this is an equivalence.
second problem: assume we are ok with the extension prolem; then a linear representation of is a vector bundle with a connection on (and we can decide to consider -connections here, but let us leave this for later). pushing this forward along produces a 1-dimensional TQFT. according to Quantization as a Kan Extension this push-forward should be a Kan extension. in paticular, at the level of objects one should have the global sections of the original bundle (note that this is the push-forward to a point of the sheaf of sections of the original bundle), and morphisms should be given by path integrals (what about taking this as a definition of the path integral?) -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010)
(what about taking this as a definition of the path integral?)
When we did the Kantization thing, there were still puzzling open questions.
I think now I have a refined idea of how the push-forward should work:
as you know, the full picture for the differential cocycles is actually not quite functors from paths to somewhere,, but twisted cocycles in the homotopy fibers of
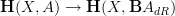
(in the case that A is a group object).
Here on the left we have the plain underlying cocycles of the bundles
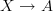 and on the right we have their curvature, which is a functor on paths:
and on the right we have their curvature, which is a functor on paths: 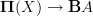 such that the underlying
such that the underlying 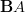 -cocycle
-cocycle 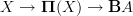 is trivial.
is trivial.Given this description, it is clear what the right push-forward should be: you push-forward both
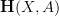 and
and 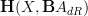 and this then induces a morphism between their homotopy fiber. That should be the push-forward on differential cohomology that we are after.
and this then induces a morphism between their homotopy fiber. That should be the push-forward on differential cohomology that we are after.So first of all, this gives manifestly the right answer on the underlying bundles, because we push the underlying bundle cocycle by itself. So a vector bundle will be sent to its space of sections, when pushed to the point as a cocycle for A the K-theory coefficient, by standard lore.
Similarly, the push-forward of the curvature bit should be clear, this must be just the fiber integration of the curvatures. For vector bundles in K-theory again, I think this should give the fiber integration of the Chern-character, as usually considered.
And then the push-forward on the differential cocycle itself is induced from this.
I haven't fully penetrated this story, but this looks right. I think it provides a missing aspect from the original Kan-tization ansatz. There the transport functors directly were pushed, not taking into account that they need to be understood as cocycles in twisted cohomology, sitting in the homotopy fiber of two other cohomology theories.
So I think this explains why the results mentiones at Kantization exhibit an unexpectedly overstrictified behaviour, it's because some additional degree of freedom in the problem wasn't taken care of. So the source of the puzzlement is really the same as that of the original "fake-flatness" puzzlement: it comes from not being serious about the fact that differential cohomology is not a plain cohomology, but a twisted cohomology theory.
-
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010)
If the God's of math would grant me one wish, it would be to have enough knowledge to understand what you just said.
My gut tells me (and has told me since you first started saying it) this is important.
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010)
it seems the God of math decided to disrupt our understanding of gauge fields by confusing our languages.. a quite old trick, it has to be said.. :-)
(or it is just me who is not able anymore to read math formulas in the forum?) -
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 8th 2010
:D
-
- CommentRowNumber7.
- CommentAuthorAndrew Stacey
- CommentTimeApr 8th 2010
Looks alright to me :P
(Okay, mea culpa. I forgot to recreate the cache so the latex plugin broke. Fixed now, I hope.)
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeApr 8th 2010
@Andrew: You rock :) Thanks
-
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 8th 2010
@Urs: so, if I'm following what you wrote, you're saying: the background field is an element in twisted cohomology, i.e. in the homotopy fibre of two cohomologies for the space . pushing both these cohomologies forward along we obtain a big commutative diagram and so a map between homotopy fibres. this map you are suggesting is the path integral, taking values into the twisted cohomology of the point.
I think I agree with this, but I'd like to spend another couple of days with the basic paths in differential manifolds/bundles with connections picture to fix my ideas in teh concrete situation, first. -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeApr 8th 2010
- (edited Apr 8th 2010)
if I'm following what you wrote, you're saying: the background field is an element in twisted cohomology, i.e. in the homotopy fibre of two cohomologies for the space . pushing both these cohomologies forward along we obtain a big commutative diagram and so a map between homotopy fibres. this map you are suggesting is the path integral, taking values into the twisted cohomology of the point.
Yes! Exactly.
but I'd like to spend another couple of days with the basic paths in differential manifolds/bundles with connections picture to fix my ideas in teh concrete situation, first.
Sure. As I said, I need to work out for myself more details of this picture. What I said was just a reply to your suggestion that the path integral might be defined as the push-forward of functors on paths. I just wanted to point out that this does not seem to be the general definition. Even though the general definition does involve this as an ingredient and as a special case.
-
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 9th 2010
- (edited Apr 9th 2010)
thinking to the special case, I've done a step backwards: from 1-paths to 0-paths. so I have a smooth manifold
 and I want to define a "functor"
and I want to define a "functor"  . looking at
. looking at  as to a category with only identities, this amonts to giving a vector space
as to a category with only identities, this amonts to giving a vector space  for any point
for any point  of
of  . so a way to make the smooth structure come into play is to define a "smooth functor" from
. so a way to make the smooth structure come into play is to define a "smooth functor" from  to
to  to be a smooth vector bundle
to be a smooth vector bundle 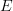 on
on  . next, I want to push forward to a point. so I want to resume all the spaces
. next, I want to push forward to a point. so I want to resume all the spaces 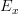 into a single one. forgetting about the smooth structure one has an obvious answer: take the direct product
into a single one. forgetting about the smooth structure one has an obvious answer: take the direct product
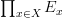 . but this is nothng but the set of sections of the projecton
. but this is nothng but the set of sections of the projecton 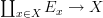 , so one can make the smooth structure come in by thinking of sections of
, so one can make the smooth structure come in by thinking of sections of 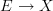 as a "smooth direct product". this is in a sense obvious, but I must admit I had never thought to sections this way before. I'd like to say this more precisely, and here is where -I suspect- differential cohomology comes in: the formal way of saying "smooth functor" is saying "a cocycle in
as a "smooth direct product". this is in a sense obvious, but I must admit I had never thought to sections this way before. I'd like to say this more precisely, and here is where -I suspect- differential cohomology comes in: the formal way of saying "smooth functor" is saying "a cocycle in 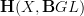 , for some suitable smooth topos
, for some suitable smooth topos  . and the "smooth direct product" is the image of this cocycle along the pushforward to the point. this pushforward, however, I must admit I don't clearly see it, so for a while I'll keep writing in terms of the naive idea of smooth functors, smooth direct products, etc.
. and the "smooth direct product" is the image of this cocycle along the pushforward to the point. this pushforward, however, I must admit I don't clearly see it, so for a while I'll keep writing in terms of the naive idea of smooth functors, smooth direct products, etc. -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeApr 9th 2010
- (edited Apr 9th 2010)
Domenico,
yes, the fact that forming the space of sections of a vctor bundle over a discrete set is nothing but taking thr direct sum of its fibers, is what was in Freed's old article on quantizatioin and higher structures part of the motivation for him to suggest that the path integral is just the top dimension piece of a more general "categorical summing operation" that expressess quantization: the space of section assigned in codimension one is itself something like a "codimension-1-path integral", namely a sum over points.
Ever since, the question has been how exactly to find from this observation the precise and fully generally working definition. That's of course what we are talking about here.
By the way, I don't see any displayed math in your latest comment. But it does display in the commentsfurther above. Maybe we need to ask Andrew for help again.
In any case, let me just see if I have understood correctly the question that you want to be looking at now: you want to consider the stack (on CartSp, I would suggest) of vector bundles --
 -- and then a manifold
-- and then a manifold  and think of a vector bundle on
and think of a vector bundle on  as a morphism of stacks
as a morphism of stacks 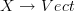 . Then you want to see in which sense this pushes forward to a morphism
. Then you want to see in which sense this pushes forward to a morphism 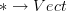 from the terminal stack on CartSp to vect, i.e. to a vector space.
from the terminal stack on CartSp to vect, i.e. to a vector space. -
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeApr 9th 2010
If so, I think then for instance the left Kan extension in the 2-category of stacks on CartSp of
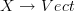 along
along  does seem to me to yield the vector space of smooth sections of the vector bundle on
does seem to me to yield the vector space of smooth sections of the vector bundle on  .
. -
- CommentRowNumber14.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 9th 2010
- (edited Apr 9th 2010)
By the way, I don't see any displayed math in your latest comment.
that was since at first I formatted the content as html (so neither I could see maths); then I reformatted it as markdown and now it should work (at least, I see maths now).
let me see if I understand what you're telling me: the naive idea of a vector bundle as a smooth functor from a manifold
 to
to 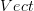 is (almost tautologically) encoded in looking both
is (almost tautologically) encoded in looking both  and
and 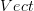 as stacks over cartesian spaces:
as stacks over cartesian spaces: 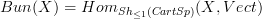 , where
, where 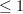 refers to the fact that we are considering 1-stacks and not arbitrary oo-stacks. in particular, since
refers to the fact that we are considering 1-stacks and not arbitrary oo-stacks. in particular, since 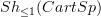 is a 2-category,
is a 2-category, 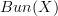 is a category, and one recovers the classical notion of morphisms of bundles.
is a category, and one recovers the classical notion of morphisms of bundles.now, given a bundle
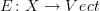 and a morphism of smooth manifolds
and a morphism of smooth manifolds 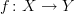 we can wonder about the Kan extension of
we can wonder about the Kan extension of 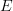 along
along 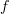 , and this we suspect is somethink like fibrewise smooth global sections.
, and this we suspect is somethink like fibrewise smooth global sections. -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeApr 9th 2010
Yes.But not “fiberwise smooth sections”. (What does that mean?) But smooth sections.
Here is the proof: let be the terminal morphism to the terminal stack on (the presheaf that assigns the one-object category everywhere).
Let be the morphism of stacks on classifying some smooth vector bundle on . Let be its vector space of smooth sections, regarded as a vector bundle over the point.
We need to show that for every other vector space , morphisms (i.e. 2-morphisms) from to are in bijection with morphisms from to .
It is sufficient to test this for the ground field. (Right?) For that case, manifestly both these sets of transformations are the set of smooth sections of .
(for this to work we need to regard as category-valued stack of course. So this here takes place in a -topos as opposed to a -topos. )
-
- CommentRowNumber16.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 9th 2010
Yes.But not "fiberwise smooth sections". (What does that mean?)
that referred to the case of a general morphism
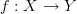 ; so my conjectural naive answer was, in that case, that over the point
; so my conjectural naive answer was, in that case, that over the point 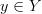 one has the vector space
one has the vector space 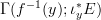 , where
, where 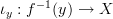 is the inclusion. actually it's likely one should work with homotopy fibres rather tahn with fibres, but let us concentrate on the case
is the inclusion. actually it's likely one should work with homotopy fibres rather tahn with fibres, but let us concentrate on the case 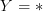 for now.
for now.now I'll go into the details of your proof here above.
-
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 9th 2010
- (edited Apr 9th 2010)
(Right?)
Right: the stack morphism is represented by the trivial bundle , and this is a direct sum of trivial bundles .
It seems I’ve finally learnt what global sections of a bundle really are :-)
-
- CommentRowNumber18.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 9th 2010
so let us take the next step and go from
 to
to 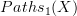 . the naive picture is that given a smooth manifold
. the naive picture is that given a smooth manifold  , a smmoth functor
, a smmoth functor 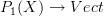 is the datum of a vector bundle on
is the datum of a vector bundle on  endowed with a connection. how can we formalize this? an obvious answer seems to look again at stacks on cartesian spaces: given
endowed with a connection. how can we formalize this? an obvious answer seems to look again at stacks on cartesian spaces: given  , one considers the internal path category of
, one considers the internal path category of  (basically we have so far been discussing it in the path-groupoid version), and stack morphisms
(basically we have so far been discussing it in the path-groupoid version), and stack morphisms 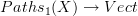 . if now we want to push this forward to the point, what we should get is again the space of smooth sections of the bundle, seen as a vector bundle over the point (and so, clearly, with the trivial connection). things become nastier if we want to go from
. if now we want to push this forward to the point, what we should get is again the space of smooth sections of the bundle, seen as a vector bundle over the point (and so, clearly, with the trivial connection). things become nastier if we want to go from 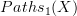 to
to 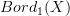 . indeed, even in the vector bundle one is considering is finite dimensional, pushing it forwrward to a point one gets an infinite dimensional vector space and so a non fully dualizable object. this obstructs the extension along
. indeed, even in the vector bundle one is considering is finite dimensional, pushing it forwrward to a point one gets an infinite dimensional vector space and so a non fully dualizable object. this obstructs the extension along 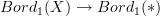 at least in a naive way. moving from paths to "measured paths", i.e., paths with a length, seems to be a solution, but I have to think more to this.
at least in a naive way. moving from paths to "measured paths", i.e., paths with a length, seems to be a solution, but I have to think more to this.quite obviously, next step would be considering
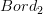 , and there for some reason I don't see yet, the right thing to do will be considering "surfaces with a conformal structure". anyway, it would qui quite senseless to represent
, and there for some reason I don't see yet, the right thing to do will be considering "surfaces with a conformal structure". anyway, it would qui quite senseless to represent 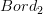 (which is a 2-category) in
(which is a 2-category) in 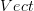 which is a 1-category, and 2-Vect seems a more suitable target.
which is a 1-category, and 2-Vect seems a more suitable target.strings here we come :-)
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeApr 9th 2010
- (edited Apr 9th 2010)
Domenico, I’ll reply directly to your last two comments later. Right now I would like to state some thoughts on the general abstract definition of “push-forward in cohomology” in the style of the intrinsic notion of cohomology of an oo-topos.
The following is supported by a handful of plausibility considerations, but might still be lacking some crucial insight, I am not sure.
Fiber-integration of cocycles
Let be an -topos.
For a fibration sequence (for every choice of base point of ) and for an -valued cocycle on , the fiber integration of over is, if it exists, a cocycle on the base ; with coefficients in the internal hom-object .
Without further extra structure, this exists canonically for the trivial -bundle over . In this case consider the adjunct of . Then the fiber integrated cocycle is the composite
of this adjunct with the transgression of the coycle to the mapping space object.
Notice that the precomposition operation produces the cocycle on which, roughly speaking, sends a point of to the integration of the cocycle on the fiber over this point.
The above construction only depends on the existence of any morphism , it need not be the identity . Call such a choice
an -orientation of . Then with respect to that we have fiber integration of cocycles as above.
-
- CommentRowNumber20.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 10th 2010
- (edited Apr 10th 2010)
apparently I’m missing something: for the trivial fibration sequence , it seems to me that is seen as a point in , and at the moment I’m unable to work out ho this reproduces the toy example of an -form which integrated on an -manifold gives a number (a 0-form on the point). there’s something crucial I must be missing :-(
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeApr 10th 2010
The basic example to keep in mind is that where and . Then the cocycle is a closed -form on the sphere. And is equivalent to the -fold delooping of , which is . So in this case the procedure I indicated is supposed to produce the “integration without integration” of the -fom over the -sphere.
One important point here is that this fiber integration procedure takes care of the shift in degree in cohomology. In the ordinary case, the push-forward of a degree -class along a map with -dimensional fibers is supposed to produce a cocycle of degree . Usually this is expresed by taking the original cocycle and sending it to the thing that evaluates on the cup product with the fundamental cycle of the fibers or something like this.
My abstract-nonsense formula above is an attempt to see what the very general mechanism behind this procedure in the context of intrinsic cohomoloy the way we discuss it here should be. But as I said, I am not fully convinced myself yet that I entirely understand this. But the above hopefully gives some indication now.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeApr 10th 2010
Domenico,
to further further expand: the basic example of fiber integration to be modeled here is that in Deligne cohomology. This is what originally my notes on transgression and “integration without integration” were getting at. A less genera-abstract-nonsense approach based however on the same intuitive idea was developed by Baer et al. A brief review of this is here in Baer on fiber integration and Cheeger-Simons characters. Notice that the main point there is effectively to take the fiber integrated cocycle to be , although the formulas there look more complicated and hide this simple idea a bit.
-
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 10th 2010
coming back to (extended) TQFTs, I’ve thought to what one earns when upgrades from paths to measured paths: a measured path can be split in two. to be more precise, let be the set of lenght paths from to , and let and be such . then composition of paths induces an isomorphism of sets
so, if is any representation (i.e., is a vector bundle with a connection on ), if one sets
(whichever meaning one is able to give to this integral), then one gets
so, if one thinks of at the “matrix element of position ” for an endomorphism of , one obtains the semigroup law . we have already remarked that in the smooth setting, the “smooth direct product” is the space of global sections, so all the informal nonsense above seems to lead to the following idea: pushing forward a linear representation of euclidean 1-bordism along produces a 1-dimensional euclidean QFT with . so, if one can see by other means that such a push-forward exists, then one can use it as a definition of the above path integrals.
(more on this tomorrow)
-
- CommentRowNumber24.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
a few other thoughts on the naive picture. when euclidean paths are considered, connected closed 1-cobordisms (i.e., copies of with a lenght) have a very simple moduli space: the half-line . evaluating the 1-dimensional euclidean QFT on connected closed manifolds, therefore produces a function on this moduli space. this can be seen as a section of a (trivial) line bundle on .
something similar happens for 2-dimensional conformal cobordism. in that case the topology of closed surfaces is completely encoded in their genus, and for each genus there is a (non topologically trivial) moduli space (this should better seen as a stack, but let us be extremely naive for now). the straightforward adaptation of the 1-dimensional argument to this case would suggest that one ends up with a funcuion on moduli spaces, but actually by the phenomenon of so-called conformal anomay one ensd up with a which is a section of a nontrivial line bundle.
what I’m convinced of, but this is still extremely foggy in my mind, is that from the right perspective this phenomenon should be not anomalous at all, and that the surprising fact should have been ending with a trivial line bundle. this perspective should involve a categorization of enriched cobordisms. for instance, in the euclidean case we have only one kind of isomorphism between Riemannian manifolds, namely diffeomorphisms mapping one metric to another by pullback. in other words, morhisms are the same as in the topological case, and preserving the metric is a constrain. in the conformal case, instead, we have a whole new bunch of isomorphsms, given by conformal transformations of the metrics. so, on the one hand, one should have the diffeomorphisms stuff which is the analougue of the topological case and so would allow mimicing everything and end up with a trivial line bundle; but then there is the conformal transformation action and its subtle interplay with diffeomorphisms to make the line bundle non-trivial. as I said, extremely foggy, but I’m convinced that when well categorized this will say that what one should expect to come out with starting with a linear representation of is a section of a nontrivial line bundle on . I mean, from the right perspective this should be the natural aswer, and not a mysterious byproduct of the particular technique chosen to give a meaning to the path-integral as it is usually find in string theory textbooks.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
Domenico,
concerning these parameterized paths, I have come to think that the following is a good picture:
let be the “parameter space” for the particle, and let be target space. Then we can consider the diagram
where the horizontal morphism encodes the action. Notice that since morphisms in are fully determined by their source and target, these serve to measure lenght: a morphism in is a path in with a length (and with a “time” associated to its source).
So here the action may have various components. Notably it may have a gauge interaction part
coming from a vector bundle with connection, but it may also have a kinetic part, which sends a path of length to the morphism (tensored with the gauge interaction part above).
If we regard as a groupoid, then we would have to “Wick rotate” this by adding an imaginary unit in the exponent, but we can also regard as paths in regarded as a Lorentzian space, then its morphisms would be futute directed paths and not invertible, as described in one of the section at Lorentzian manifold. In this latter case would really be spacetime, not just space, and we would add a square root in the exponent and end up with the action for the Klein-Gordon particle.
We have the canonical point and can form the lax pullback of that along the action, to obtain a diagram
This is the groupoid that is described at “exercise in groupoidification – the path integral” (it is roughly – but not exactly – something like an Atiyah-groupoid, therefore my symbols). Its objects are vectors in fibers of and its morphisms are path in with length, that go from one vector in one fiber to the corresponding result of parallel transport/kinetic action of that vector along the path to another vector in another fiber.
Think of an -groupoid under -groupoid cardinality as a rational number. An -groupoid over a fiber of is a collection of rational numbers over elements of the vectors in the typical fiber of - By multiplying and adding this all up in this defines a vector in . So an -groupoid over the space of objects of decategorifies to a section of , a wave function. Pull-pushing this -groupoid over the space of morphisms of is precisely the path integral, as described at “exercise in groupoidification”.
-
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
rather than , I would consider a whose 1-morphisms are pairs , where is a map from a 1-manifold to , and is a Riemannian metric on that 1-manifold (this is clearly reminiscent of Polyakov way of looking at string actions). then one would have a diagram
where is the moduli space of Riemannian 1-manifolds (i.e., the datum of topological type and lenghts). this is almost the same thing as , so I guess I can verbatim follow your argument to end up with a diagram like
which is of the shape I was seeking. I guess “an exercise in groupoidification – the path integral” refers to the nCafe’ entry and not to the NLab one, right? is there a cleaned up version of that? (otherwise i can clean it up or the Lab, I can’t imagine a better way to learn things contained there). a final question: by the canonical you mean the morphism picking up the base field?
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
I guess “an exercise in groupoidification – the path integral” refers to the nCafe’ entry and not to the NLab one, right? is there a cleaned up version of that? (otherwise i can clean it up or the Lab, I can’t imagine a better way to learn things contained there).
I am right now in the process of cleaning up the nLab entry exercise in groupoidification - the path integral. Right now it is however back in birth state. You can see the history links to get the previous version, of course.
a final question: by the canonical you mean the morphism picking up the base field?
Yes.
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
rather than , I would consider a whose 1-morphisms are pairs , where is a map from a 1-manifold to , and is a Riemannian metric on that 1-manifold (this is clearly reminiscent of Polyakov way of looking at string actions).
We can do that. For the present purpose this is equivalent to what I porposed, because you can think of a path to the (pseudo)Riemannian manifold as providing via pullbacl of the metric on a metric on .
I am thinking that for further developments thinking of will be more beneficial. But maybe I am wrong. And for the time being it does not matter much. So for the purpose of the discussion we can think of either definition.
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
By the way:
One indication hat should be considered is the material at multisymplectic geometry.
-
- CommentRowNumber30.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
you can think of a path $\gamma_\Sigma : [0,1] \to \Sigma$ to the (pseudo)Riemannian manifold $\Sigma$ as providing via pullback of the metric on $\Sigma$ a metric on $[0,1]$.
Sure, and in string parlance this would be a Nambu-Goto point of view. this is classically equivalent to the Polyakov point of view which adds a metric on the source as an independent field, but since this second point of view seems to be more fruitful when computing string path integrals, I would adopt it from the beginning. anyway, since at this level the two approaches can be considered equivalent, I agree: let us think of either definition.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
you can think of a path to the (pseudo)Riemannian manifold as providing via pullback of the metric on a metric on .
Sure, and in string parlance this would be a Nambu-Goto point of view.
Not quite. For the Nambu-Goto point of view I would pull back the metric from . Here I am pulling it back from , which already is the worldsheet!
I think rather what I am getting at there is a distinction not usually made: that between parameter space and paths in parameter space.
My motivation here is to get to the setup in my AQFT paper: i know that a parallel transport on the path (n,1)-category of a Lorentzian worldvolume induces a local net of observables, hence an AQFT on . That is similar to a factorization algebra on , which is known to be related to cobordism reps by topological chiral homology, at least in the topological and Euclidean case. But here I find it interesting to really deal with the physical/non-topological and Lorentzian case. So I want a quantization prescription that sends a differential cocycle on target space to one on paramater space .
Anyway, i have continued working on exercise in groupoidification - the path integral a bit more. This is not yet in the form of a good exposition. But you will be able to follow it.
-
- CommentRowNumber32.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
a remark on the definition of the groupoid in #25.
given a group , a set endowed with a -action is the same thing as a functor . building the action groupoid can therefore be seen as a map . exactly the same thing happens for : one starts with a representation and ends up with a groupoid . and the analogue of the fibration sequence is the square
where is the vector bundle defined by (forgetting the datum of the connection).
edit: ok, I see this is already discussed at the nCafe’ exercise in groupidification. I’ll wait I finish reading that before coming back here.
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
seen as a map
Sorry, could you say that piece again? This is probably a typo, I guess. I am not 100% sure how it should be read.
-
- CommentRowNumber34.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
The map (presumably a functor) is the assignment
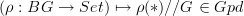 . This functor could be lifted to
. This functor could be lifted to 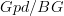 , if desired, and it probably should be.
, if desired, and it probably should be. -
- CommentRowNumber35.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
that should have been , there was a missing arrow :)
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
Oh, I see. That functor is called the hocolim, by the way! The action groupoid is the oo-colimit over the action functor.
-
- CommentRowNumber37.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I’m on the nCafe’ blog entry now. the first post ends with
So the “total” space of over is the -colored set , where I write for an element colored by . If has an additive structure, for instance if it is a vector space, we have the cardinality operation on -colored sets and get that the cardinality of the above is . But that’s the right path integral kernel for propagation from to acting on the state over .
I totally agree, but maybe instead of -colored sets, I would first talk of sections of bundles. more precisely, let us denote by and the copies of sitting over and respectively. then the total space of over can equivalently be seen as the constant section of the trivial -bundle over , or as the (“nonconstant”) section of the trivial -bundle over . then, precisely since the bundle we are considering is trivial, a section of its is just a function , and so a -colored set. The “measure” of this -colored set is , i.e. the above written sum in the discrete case.
-
- CommentRowNumber38.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
just to see if I’m following the span of groupoids idea: if is a morphism of groupoids, then I have both simple and natural pullbacks and pushforwards . the first is defined by ; the second is just the composition .
so, in particular, given a span of groupoids , we have a push-pull .
is this correct?
-
- CommentRowNumber39.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
@Domenico
Yep!
-
- CommentRowNumber40.
- CommentAuthorzskoda
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
A general remark I always like to emphasise: the pushforward in the span/correspondence tricks whenever things have problems with size is the proper pushfoward rather then the usual pushfoward in all geometric situations I know of. This is related to the ability to integrate (“integral transform”, “cardinality”) what you can do only if you correctly control compactness by teh appropriate version of properness. Of course, the rarely used alternative to use the non-proper pushfoward but then to restrict the attention to the sheaves which behaves well with respect to it, as if the map/pushforward were proper, i.e. to work with proper sheaves/objects only.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
Domenico writes:
I totally agree, but maybe instead of V-colored sets, I would first talk of sections of bundles.
I think I see what you mean, but does this generalize well to the case where we do not start the pull-push with a “delta-state” but with a general state?
The most general picture is that we pull-push any “geometric oo-functions” along the span. Overcategories of sets of groupoids or oo-groupoids are just the simplest example of that. Maybe it is evenn good to apply the oo-Grothendieck construciton and think equivalently not of oo-groupoids over the spaces of fields being pull-pushed, but oo-sheaves on these spaces o fields. I am not sure yet if I have found the most elegant perspective here.
just to see if I’m following the span of groupoids idea: if f:A→B is a morphism of groupoids, then I have both simple and natural pullbacks
Yes. More generally speaking, we make use of the fact that forming overcategories is a geometric function object as discussed there in more detail.
Zoran writes:
A general remark I always like to emphasise: the pushforward in the span/correspondence tricks whenever things have problems with size
Yes, that’s a good comment. Generally one might amplify the “size” issues here (which are about finite versus infinite,not set versus class here): in what we are dewscribing, all the subtlety with the non-well-definedness of the path integral is pushed into a decategorification step, that which takes cardinalities of oo-groupoids over . If this step is postponed ad infinitum then the problem that the path integral does not produce a well defined number never appears.
There are different conclusions one might eventually draw from this, of course, but for the time being it is useful to just notice this fact.
-
- CommentRowNumber42.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
so, I’ve been thinking to “paths with absolute time”, i.e. what in Urs picture is . if I’m right in interpreting it, the idea is that objects are pairs , where is a point of at time and morphisms are paths such that and . this way one is able to “break a path at intermediate times” and to obtain the 1-parameter group discussed in #23.
I’m wondering whether this is nothing but a simplified version of a spacetime manifold , in which one has “factored out” the time component. then one is parametrizing worldlines using absolute tiem as a parameter. is it so?
-
- CommentRowNumber43.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
if I’m right in interpreting it
yes.
I’m wondering whether this is nothing but a simplified version of a spacetime manifold , in which one has “factored out” the time component.
No, we want to think of as being Lorentzian spacetime. Rather, here and generally is the extended configuration space as discussed in multisymplectic geometry. This is really an important motivation for considering it. Please have a look at the entry on multisymplectic geometry.
-
- CommentRowNumber44.
- CommentAuthorEric
- CommentTimeApr 12th 2010
The shift to Lorentzian spacetime makes me happy. That was one of the things that bugged me about the original “Kantization”. I asked at An Exercise in Kantization:
Eric: “Let be the groupoid which has as objects pairs , where and , and as morphisms paths of proper time .”
Why do we consider groupoids here? I wouldn’t expect paths to have “inverses”, I’d expect them to have “adjoints” or maybe “opposites”.
Shouldn’t there be a partial order somewhere related to causality?
-
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
Yes, Eric, right, you had a good point back then, I am now headed firmly in this direction.
However, as i said before, the main provblem with the Kantization approach was that it didn’t realize differential cocycles in twisted cohomology, hence didn’t disstinguish “orbifold morphisms” from “paths”. In the new version of exercise in groupoidification - the path integral this is now imporved. Unfortunately, it also makes the discusison more involved. I’ll try to give a better exposition later. Maybe later today.
-
- CommentRowNumber46.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
I’ve completed reading through the nCafe’ entry. there is an 11 points road map to path integrals. steps 1-7 are worked out in full detail (at least in a discrete toy example, with a trivial vector bundle ove , but let us play with this for time being). then we have:
Step 8) Pull back a V-colored set along the map “in” Step 9) Push-forward a V-colored set along the map “out” Step 10) There it is – the path integral Step 11 +) The canonical path integral measure from the Leinster measure/ groupoid cardinality
steps 8-9) should be just a particular case of push-pull described in #38 and (more precisely) in #41 above, so these two steps should be ok. (thanks Zoran for the vs. remark)
step 10) should be taking V-cardinality of the last V-colored set one finds, so also this step should be ok (by the way, I’m now convinced that a section of a trivial bundle is a particular case of V-colored set, but are these latter who behave well under push-pull, so I’m converted to the V-colors now).
step 11 +) seems to be completely missing at the moment. where do I look for it?
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
step 11 +) seems to be completely missing at the moment. where do I look for it?
Section 1.4 here has some remarks. But a really good writeup I have not produced so far.
Well, maybe I am right in the middle of producing it, there is this article that Zoran is pushing me to finish, which I should be doing right now instead of posting to the nForum…
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
But Domenico,
as far as the recipe goes, there is no new step: we still just form the pull-push, and the formalsim takes care of everything. All we may have to do is identify the result as really being what is discussed in other language in the literature.
Notably, say in the the example of DW theory, the field configurations
is a nontrivial groupoid, so as we pull back groupoids to this, we pick up a copy of this groupoid with its automorphisms.
Let’s look at the most simplified setup where there is a single point and a single path starting at that point, but that path has automorphisms, so is a . Then for an -groupoid over the point, we pull-push it through
and obtain the groupoid over the output point. So the groupoid cardinality coming from of that will differ from that of by factors one over . That’s really what that groupoid-cardinality/Leinster measure thing is about.
The punchline is that if we set up the pull-push correctly, then there is no extra step involved.
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
Domenico,
it is kind of remarkable that you are the first person apart from a very small number that I talked to in private, from whom I have an indication that he or she has read my article “exercise in groupoidification” and understood it.
I don’t know if this means no-one else understood it (I can’t imagine that), but at least I never got any feedback from someone who understood it.
-
- CommentRowNumber50.
- CommentAuthorEric
- CommentTimeApr 12th 2010
From here:
This Lorentzian path (∞,1)-category is roughly described as follows:
its space of objects is ;
the elements of its space of morphisms are generated from
morphisms given by smooth spacelike curves ;
morphisms of the form for every in the causal structure of .
Why do these curves need to be smooth? Couldn’t they just as well be lightlike random walks? Or, why isn’t the second bullet sufficient?
-
- CommentRowNumber51.
- CommentAuthorEric
- CommentTimeApr 12th 2010
it is kind of remarkable that you are the first person apart from a very small number that I talked to in private, from whom I have an indication that he or she has read my article “exercise in groupoidification” and understood it.
I don’t know if this means no-one else understood it (I can’t imagine that), but at least I never got any feedback from someone who understood it.
That’s why I’m so happy Domenico is here :) I wish dearly that I could understand. If two people on the planet understand it, the chances I will someday increases :)
I’m not quite sure it is THE answer, but it rings of truth.
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
Why do these curves need to be smooth? Couldn’t they just as well be lightlike random walks? Or, why isn’t the second bullet sufficient?
There is quite a bit of flexibility here. When you look at the constructon in From FQFT to AQFT, you see that all that really matters is that (in 2d) spacelike separated points are connected at all. (See also the remarks on the time-slice axiom).
But the second bullet alone won’t be sufficient, because here is it crucial that these morphisms are future-directected paths.
The main point is that the 2-cells are, in one way or other, regions “of spacelike width and future-directed height”. That’s what makes any 2-functor on this induce a local net of observables.
-
- CommentRowNumber53.
- CommentAuthorEric
- CommentTimeApr 12th 2010
I think I get your point. If all we had was for , then we could have spacetime looptie loops :)
So why not let be a directed space? Then the only way would be if the path was future directed and the second bullet would be sufficient (I think).
-
- CommentRowNumber54.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
Urs #49, Eric #51, I’m flattered! :)
now I feel obliged to write something here on Diijkgraf-Witten and Yetter models, which could hopefully interest you (I’ve just read section 1.4 from Urs paper and fell in love for these toy models :) )
but I’m going out for a while. will be back this evening.
-
- CommentRowNumber55.
- CommentAuthorEric
- CommentTimeApr 12th 2010
now I feel obliged to write something here on Diijkgraf-Witten and Yetter models, which could hopefully interest you
Oh! Oh! Please :) That would be awesome.
I’ve just read section 1.4 from Urs paper and fell in love for these toy models :)
By the way, why do people insist on calling these “toy models”? What if the continuum turned out to be the toy model and these finitary models actually turned out to be more fundamental? Bias! :)
-
- CommentRowNumber56.
- CommentAuthorEric
- CommentTimeApr 12th 2010
I’ve just read section 1.4 from Urs paper and fell in love for these toy models :)
By the way, which paper?
-
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I’ve just read section 1.4 from Urs paper and fell in love for these toy models :)
By the way, which paper?
Mentioned in #47: these notes.
Please note that these are old notes that have meanwhile be superceded by better stuff. In the unlikely case that you feel an urge to run around and show this to other people, then please check back with me first and I provide links to imporved accounts. Except for instance for that section 1,4 there
So why not let X be a directed space? Then the only way x≤y would be if the path x→y was future directed and the second bullet would be sufficient (I think).
No, somehow it seems I haven’t yet communicated yet what I have in mind. A Lorentzian manifold is a directed spac eof sorts, already, which is exhibited by the fact that its Lorentzian path (oo,1)-category is indeed that: an (oo,1)-category not all whose morphisms are invertible.
Also closed timelike paths are not the problem here, everything I want to do can be done for Lorentzian spaces that are locally globaly hyperbolic (as discussed in the last section of my article).
No, as I meant to say before, the crucial point is that causal subsets appear as top-dimension morphisms.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
By the way (to Domenico or Zoran, or whoever is listening): where in the new version of exercise in groupoidification - the path integral I start using the pushout 2-categiry , things get a bit sublte, as always when forming colimits of n-categories. I think what I am claiming is correct, but a careful reasoning requires a bit of care here.
-
- CommentRowNumber59.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
I wrote:
I think what I am claiming is correct,
No, it’s not. I’ll rework the entry now to fix this, by falling back to “fake-flat” n-transport. Then it works again. It’s sufficient for the example with abelian gauge group anyway, but I had hoped it would work more generally. But maybe not.
-
- CommentRowNumber60.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
I’m now on Diijkgraaf-Witten model in Section 1.4 from Urs. there’s a point where I’m confused. on page 10 one reads
To make this technically more easily tractable without losing any information, we may choose a point in each connected component of and let be instead the full subgroupoid of the fundamental groupoid on these chosen points. That makes the parameter space groupoid and hence also the configuration space groupoid a finite groupoid.
does this mean that for one has the terminal groupoid? I guess no, otherwise I would be confused by
a few lines later, which I interpret as a (higher-)groupoid version of the topological equivalence .
need help
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
Domenico,
That's not well written and possibly subject to errors, as I see.
We should be looking at morphisms
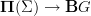 in the category of smooth
in the category of smooth  -groupoids. A priori this can be done choosing a Chech groupoid for
-groupoids. A priori this can be done choosing a Chech groupoid for 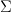 , but since
, but since 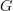 is finite a much smaller finite model is sufficient, obtained from a triangulation of
is finite a much smaller finite model is sufficient, obtained from a triangulation of 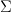 .
.In modern terms I would say: by adjunction
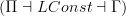 and definition
and definition 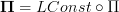 we have that
we have that 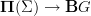 is adjunct to
is adjunct to 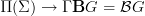 , where
, where 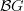 is supposed to denote the bare groupoid, and I am using that
is supposed to denote the bare groupoid, and I am using that 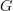 is discrete. Here we may pick a finite equivalent model for
is discrete. Here we may pick a finite equivalent model for 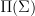 .
.Sorry, that writeup you are looking at is probably really badly written.
-
- CommentRowNumber62.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
wait. you’re saying that what there (in section 1.4, I mean) is should rather be , right? (by the way, this would make almost-trivially true)
-
- CommentRowNumber63.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
should rather be , right?
Yes.
…almost-trivially true
Yes.
Meanwhile, I have thought about how to construct that groupoid over that enters the “exercise on groupoidification” in a better way. But I need to do a telephone call first…
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I corrected that statement that involved pullback over that pushout category at “exercise in groupoidification”.
I try to bring the entry into better shape, but here the key point:
define to be the category given by the ordinary pullback
where is the interval category, the functor category and picks the ground field vector space. Via the remaining map this maps to and then further to .
We want to pull back
along our differential cocycle to , i.e. form the pullback of the diagram
Over this is nothing but the total space of the vector bundle over , pulled back to . Over this should now correctly be the groupoid as stated before: objects are triples – a vector in the fiber over , and morphisms are paths in and , taking to , where is the corresponding parallel transport.
Notice, crucially, that the nontrivial 2-morphisms in drop out in the pullback, as there are none in . So it comes out nicely.
The only point that I am now wondering about is what intrinsic oo-categorical construction this models. I mean, we know that over the ordinary pullback of models the lax pullback (really: comma object) of the point. But in the above construction it is key that is also used over , instead of . This means that we are computing some lax pullback (or rather comma object) of the point in , but subject to some constraint. I am not sure yet how to state that fully intrinsically…
-
- CommentRowNumber65.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
still playing with baby toys. Dijkgraaf-Witten, at the moment. I’m now convinced that a way of looking at that is as to a manifestation of the homotopy hypothesis at its best. let me explain what I mean by making a step backwards and going from baby toys to toddler toys: finite group cohomology.
here we have a finite (or discrete) group , and a discrete abelian group , and we want to define . a way of doing this is to realize everything topologically: from we build the classifying space , and from the Eilenberg-MacLane space . then we consider the space of maps (these are our cocycles) and take its .
this way we have a in a certain sense familiar (topological spaces, continuous maps, homotopies,..) description of the set . the drawback is that the topological spaces involved here are “gigantic” (infinite dimensional CW-complexes), where we had started with a very “little” datum: a finite group. so one can wonder if there is a finite model for the above construction, and the homotopy hypotesis serves it on a silver plate. namely, since is discrete, is a 1-type, and nothing but the topological realization of the delooping groupoid (boldface here); similarly is the topological realization of the -groupoid , and the space of cocycles is . since is a finite group, is a finite groupoid, and so is a finite set. this set is the finite model for we were looking for.
now, the Dijkgraaf-Witten model (in the next post)
-
- CommentRowNumber66.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
Domenico,
so far: yes, exactly. I suppose you know it, but this story is also at group cohomology.
-
- CommentRowNumber67.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
yes, indeed I knew: I was reporting it here planning to write a post on Dijkgraaf-Witten as self-contained as possible, but I had to quit writing, and so it remained half-way. I’ll write the second part in a couple of hours.
-
- CommentRowNumber68.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
ah, then please consider typing it into Dijkgraaf-Witten theory
-
- CommentRowNumber69.
- CommentAuthorEric
- CommentTimeApr 13th 2010
No worries. With “Source” he can type it anywhere he likes. I’ll copy over anything that appears here :)
-
- CommentRowNumber70.
- CommentAuthorEric
- CommentTimeApr 13th 2010
Just to prove that I’m not just saying that, I added Domenico’s comment above about finite group cohomology to Dijkgraaf-Witten theory :)
-
- CommentRowNumber71.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
No worries.
Not worried, just busy. I could do all this myself – if the day had more hours. Thanks for your helpl. I added some hyperlinks.
-
- CommentRowNumber72.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
- (edited Apr 13th 2010)
so, the Dijkgraaf-Witten model.
here the topological picture can be given as follows. we have a parameter space , a finite group , and cocycle (note that since we are looking at as to a discrete group here, this cocycle corresponds to a flat 3-bundle over . similarly, a map is the datum of a flat -bundle over .
then we have the following diagram of topological spaces
push-pull along this diagram gives a homotopy class of maps . this uses in an essential way the fact that the set of homotopy classes of maps is an abelian group, namely . in particular, for we obtain an element of .
(to be continued. it seems today I’m unable to find time for writing. hopefully this evening (for European readers))
-
- CommentRowNumber73.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
- (edited Apr 13th 2010)
(note that since we are looking at
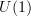 as to a discrete group here, this cocycle corresponds to a flat 3-bundle over
as to a discrete group here, this cocycle corresponds to a flat 3-bundle over 
Yes. Though I would like to phrase this as follows, which works even assuming we regard
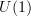 with its standard smooth structure.
with its standard smooth structure.We are working in the locally contractible (infinity,1)-topos of oo-sheaves on CartSp. As discussed at path oo-groupoid (schreiber) we have there apart from the definition
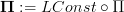
also the relation
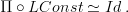
Now,
 being discrete means that for
being discrete means that for  its bare delooping groupoid, we have
its bare delooping groupoid, we have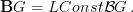
Because an oo-stack on CartSp being constant means nothing but that regard as a Lie
 -groupoid it has the discrete smooth structure.
-groupoid it has the discrete smooth structure.So with the above it follows that
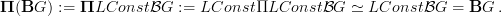
So every smooth principal infinity-bundle on
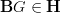 extends necessarily and uniquely to a flat principal oo-bundle, along the constant path inclusion
extends necessarily and uniquely to a flat principal oo-bundle, along the constant path inclusion 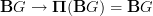 .
.There are a handful of such statements which all follow just from formal manipulations of the triple of adjoint oo-functors provided once we have a locally contractible oo-topos.
-
- CommentRowNumber74.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
I’ve added a couple of comments in post 72 above, by editing it. have to go now.
-
- CommentRowNumber75.
- CommentAuthorzskoda
- CommentTimeApr 13th 2010
I have placed the link in the Latest Changes, but regarding that Urs’s part overlaps with the topic of this discussion, let me anounce also here that the overview paper on categorical symmetries in mathematical physics which Urs and I published last year (written in Dec 2008) is now being expanded just slightly for the arxiv. The nlab page for it is Categorified Symmetries (zoranskoda). Roughly the early part of the paper is mainly written by me, and the later by Urs and has much overlap with other things Urs has been doing, cinluding his paper with Sati and Stasheff and our big “nactwist” preprint.
In latest changes discussion, I also posted a question on surpressing automatic numbering in the toc which I cut and pasted from the pdf and it displays wrongly. Any suggestions and corrections are welcome.
-
- CommentRowNumber76.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
- (edited Apr 13th 2010)
Right. Domenico, I hope this doesn't come across weird now. I hope I did mention that I am busy finishing up some notes with Zoran, that have some overlap with the discussion here. It's of course hardly a coincidence, really.
-
- CommentRowNumber77.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
ok, I’ve got it, it’s easy!
we start with the background field . then we transgress it to , i.e., we apply the functor. this way we get a morphism . passing to connected components we get a function , i.e., a function
since is an abelian group, once we fix a measure on the set , we can integrate to get an element in .
so the only problem left is how to choose the integration measure. the right choice consists in looking at as the set of isomorphism classes of objects in the oo-groupoid . then we have a canonical measure on this set: the Leinster measure.
next step consists in translating this topological description into a oo-groupoidal one, which will turn out to be completely explicit and combinatorial.
-
- CommentRowNumber78.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
Urs, how could that come across weird? just do not worry about :)
-
- CommentRowNumber79.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
- (edited Apr 13th 2010)
how could that come across weird? just do not worry about :)
Okay, good. I have had funny experiences with some people concerning verbal exchange of ideas. I didn’t think you are one of them, but since then I am being very cautious. Or at least very nervous. :-)
Anyway, I hope we once write some article together, you and me.
Now concerning your integration prescirption above:
Yes, I meant to indicate further above that this comes out automatically from the pull-push-prescription:
take your to be part of a span and hom that into . Actually, you should really be homming it into that bundle over which further above we called the Atiyah groupoid (though that wasn’t a good name), but a map into will be part of it. Then you are to pull-push sections through this, in terms of -groupoids over these hom-groupoids. This does what you just described in words: it sums up all values of the transgressed background field and divides (after taking groupoid cardinality ) by the automorphism groups.
If you see what I mean. I should finally write that out formally, I guess…
-
- CommentRowNumber80.
- CommentAuthorzskoda
- CommentTimeApr 13th 2010
Igor Sharygin and I are working (now with big breaks already for a year) on a small project concerning algebroids. In fact there is a PBW theorem there which is classical and is of course related to sort of formal exponential map. Thing which may be interesting to the people in the line of this discussion is that we are trying to use a connection on the algebroid (if it is given) to CORRECT the symmetrization map (effectively correcting the exponential map hence). I want to use that for some problems of quantization. I hope the work can have enough descent form to post some of it to nlab (now it is still in a messy phase) by say early next month…
-
- CommentRowNumber81.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 13th 2010
Urs, so you’re saying that what I’ve been describing so far is the vacuum-to-vacuum expectation corresponding to the manifold with no boundary . next step is to build an extended 3-dimensional TQFT, of which what I described above is just the tip of the iceberg. ok, let’s do that.
at the present I have oly a very vague idea of how things should work: the background field is the datum of a 3-bundle with a (flat) connection, so we have -transport functors for , and we can use these to define operators between sections which look like “the sum over all manifolds spanning between two boundary data”. need to think more on this.
-
- CommentRowNumber82.
- CommentAuthorUrs
- CommentTimeApr 13th 2010
Urs, so you’re saying that what I’ve been describing so far is the vacuum-to-vacuum expectation corresponding to the manifold with no boundary Σ. next step is to build an extended 3-dimensional TQFT, of which what I described above is just the tip of the iceberg. ok, let’s do that.
That’s true, I should have said it along these lines, yes. What I kept getting is is producing the actual propagation functor. By the way, the canonical reference to see what this functor should be is Freed-Quinn.
at the present I have oly a very vague idea of how things should work: the background field is the datum of a 3-bundle with a (flat) connection, so we have n-transport functors for n=1,2,3, and we can use these to define operators between sections which look like “the sum over all manifolds spanning between two boundary data”. need to think more on this.
Yeah, I am also still lacking the fully extended picture, that goes down to the point starting from the kind of data we are talking about. I think what I sketched so far gives the Freed-Quinn propagation 1-functor. But there should be a nice way to go all the way to the point .Towards the end of that writeup with Zoran there are some reemarks on how for instance the modular tensor category should appear along these lines, which is what the DW theory is supposed to assign to circles. But I am lacking a fully coherent full picture, still.
-
- CommentRowNumber83.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 14th 2010
I have a sort of geometrical picture in mind, but I lack a crucial final step related to integration-without-integration. let me try explain what I miss. if is a closed (compact, oriented) -manifold, I’d like to think of a map as a closed real -form on . I can integrate by first looking at it as an element of and then taking its isomorphism class, i.e. . ok, fine and elegant :) but if is a closed -form, then I can integrate it not only on the whole , but also on a d-simplex of . this time, clearly, looking at and then taking the isomorphism class would not work, since . however, if we consider relative cohomology instead, we find , and this very mich looks liked the seeked integration-without-integration. so, what I miss is: can I see relative cohomology in terms of homotopy classes of maps relative to ?
If so I’d be very happy.. :)
-
- CommentRowNumber84.
- CommentAuthorEric
- CommentTimeApr 14th 2010
I know you guys are working on a “toy model”, but I keep wondering if there is a “toy toy model”. Instead of a finite group on a smooth manifold, what about a finite group on a finite discretized space, e.g. a grid of something? Would you then be able to do all this with matrices?
-
- CommentRowNumber85.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 14th 2010
well, the idea should be that for what concerns here, a smooth manifold can be thought of as a discretized space, e.g., by considering a triangulation of its. computations with the discrete model are the ones on the oo-groupoid side, while “continuous computations” are those on the topological side. the equivalence of the two models then gives the following magic trick: whichever triangulation one takes, the resutl of the discrete computations will be the same :)
(the toy toy toy example of this is the computation of cellular cohomology vs. singular cohomology)
-
- CommentRowNumber86.
- CommentAuthorUrs
- CommentTimeApr 14th 2010
- (edited Apr 14th 2010)
Domenico,
yes. Yes.
I believe that relative cohomology in an
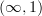 -topos
-topos 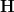 is the hom-complexes in the arrow-category
is the hom-complexes in the arrow-category 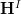 . That's what I have been using to describe twisted differential cohomology, which is flat differential cohomology with some coefficients, relative to the constraint that restricting to constant paths makes this land in more restrictive coefficients.
. That's what I have been using to describe twisted differential cohomology, which is flat differential cohomology with some coefficients, relative to the constraint that restricting to constant paths makes this land in more restrictive coefficients.So here in your case, the relative cohomology is
![\pi_0 \mathbf{H}^I([\partial \Delta^n \to \Delta^n, \; * \to \mathbf{B}^n \mathbb{R}])\,. \pi_0 \mathbf{H}^I([\partial \Delta^n \to \Delta^n, \; * \to \mathbf{B}^n \mathbb{R}])\,.](/extensions/vLaTeX/cache/latex_108f96d22c4ae1f015c188f7d24cfbe8.png)
By the way, I am tinking that in the context of quantization, this, too, can usefully be understood in terms of homming cobordism cospans into something, which really means homming
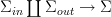 into something. For path integral quantization, we fix the states on these boundaries
into something. For path integral quantization, we fix the states on these boundaries 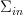 and
and 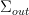 and do some integral over all values in the thing
and do some integral over all values in the thing 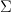 in the middle. That means working in relative cohomology.
in the middle. That means working in relative cohomology. -
- CommentRowNumber87.
- CommentAuthorUrs
- CommentTimeApr 14th 2010
I once started an entry on this relative cohomology in an oo-topos at relative cohomology (schreiber), but didn't develop that entry much further.
-
- CommentRowNumber88.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 14th 2010
By the way, I am tinking that in the context of quantization, this, too, can usefully be understood in terms of homming cobordism cospans into something, which really means homming \Sigma_{in} \coprod \Sigma_{out} \to \Sigma into something. For path integral quantization, we fix the states on these boundaries \Sigma_{in} and \Sigma_{out} and do some integral over all values in the thing \Sigma in the middle. That means working in relative cohomology.
that’s exactly what I had in mind. but without identifying homotopy classes of maps with fixed boundary conditions with relative cohomology I wasn’t able to make sense of integration (I mean, standard integration with an abelian group as target). now I can write another bit of the topological picture :)
-
- CommentRowNumber89.
- CommentAuthorUrs
- CommentTimeApr 14th 2010
- (edited Apr 14th 2010)
Eric writes:
I know you guys are working on a "toy model",
This is in fact a misinterpretion. On the contrary, what Domenico and I are discussing here is the question how to work in as mind-boggling-generality as possible!
To the extent that it works and is understood, we are talking here about internalizing quantization of differential cocycles to sigma-model QFTs in any suitable (oo,1)-topos! Where suitable probably means precisely: locally contractible.
We are just cross-checking here the very general development with special well understood examples, as a guiding light. DW theory happens to be the Drosophila fly of TQFTs: close to being as simple as possible while still being interesting enough to serve as a template for the general case. So we are cross-checking against that.
-
- CommentRowNumber90.
- CommentAuthorEric
- CommentTimeApr 14th 2010
I wouldn’t be excited about this conversation if it were merely about toy models :)
I have some philosophical/ontological gripes, but I will save those for another day :)
-
- CommentRowNumber91.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 14th 2010
Urs, do not frighten Eric with locally contractible (oo,1)-topoi.. our flies are posing a quite general question at the moment: which is the vector space DW-theory is supposed to associate with a surface? the original Dijkgraaf-Witten paper is extremely elusive on this point. they say there must be some Hilbert space associated with a surface , but this is never explicitly defined. the only thing they say is that it should be a “quantization” of the phase space given by the set of isomorphism classes of of -bundles over and that, despite one could naively expect that , this dimension in general only satisfies . here the dimension of is computed without knowing what is using the standard TQFT trick of computing the 3-manifold invariant for the closed 3-manifold .
in the topological description of DW we are pursuing here, it is convenient to think of as .
a vague indication of what could be is given by the bit of definition of the linear mapping associated with a bordism . they say that “for fixed morphisms and , the kernel of is given by
where the summation is over those that restrict to and at the boundaries.” here is the 3-manifold (with boundary) invariant associated with an homomorphism .
despite having no clear idea of what should be, the above formula for matrix elements admits a simple and clear expression in terms of the topological picture used in previous posts. namely, consider the inclusion (and assume is connceted). for a fixed map , consider the relative hom-space
and use the cocycle to transgress this to a map
where the fact that a map from a 2-dimensional manifold to is homotopy equivalent to a constant map has been used. passing to ’s we find
(here we used integration without integration). finally we integrate this map over to get the element in .
-
- CommentRowNumber92.
- CommentAuthorUrs
- CommentTimeApr 14th 2010
- (edited Apr 14th 2010)
Yes, that looks good, something like that. Maybe you need an extra constraint on the relative cohomology to ensure that in
the top part of the commuting diagrams is really the identity. What you really want at this point is morphism in the undercategory .
But apart from such details, yes, that should be the way it works. One should find the fully systematic prescription behind these kind of operations.
If we do start with a notion of 3-vector space – something like a weak algebra object in the category of bimodules for instance – and pick a representation , then the “exercise in groupoidification”-prescription is supposed to give this. But it’s a bit tedious to unwind…
-
- CommentRowNumber93.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 14th 2010
- (edited Apr 14th 2010)
I agree we should pick up some representation . however, this datum is apparently missing in the original DW paper, so I guess there shoud be some notion of defining representation of implicitly used (the 3Vect analogue of the fact is the defining representation of the group ).
in the meanwhile I’ve been thinking to the DW argument to exclude some of the isomorphism classes of -bundles over the surface from the generators of the vector space (in their words: “So in that case the bundle over described by does not contribute a quantum state, and the dimension of the Hilbert space is smaller than expected.”) in the topological picture I’ve been trying to describe so far, this should read as follows: the space has several distinct connected components. for each component there is a 1-dimensional representation of , and only components for which this representation is trivial survive.
despite this interpretation is a very rough idea, I can see something good in it: we are looking at the set , which is supposed to be a basis for not as a bare set, but as something which remembers its groupoidal origin. mmm.. looks like having a collection of ’s and over each one a rank 1 vector bundle; of this bundle one takes -invariant sections, so only the trivial -actions survive. but his one should be able to say this more intrinsically, without choosing the representative basepoints which reduced the groupoid to the form . namely, one should have a natural line bundle over the groupoid, and invariant sections should be considered. I must have read something like this in Freed-Quinn paper.
-
- CommentRowNumber94.
- CommentAuthorTim_Porter
- CommentTimeApr 15th 2010
I had not been following this thread, but it looks as if I should. I have been trying to understand the construction by Turaev of a primitive cohomological HQFT given a cohomology class in $H^{d+1}(G,K^*)$. All of his vector spaces are of dimension 1, and he twists things using the $d+1$-cocycle at the level of a basis choice. He says he adapted the method from Freed-Quinn.
(The method is simple to apply and quite clear in his 1999 HQFT paper. I have been trying to fit it into the framework of a `relative' TQFT as I put forward some time ago in a research proposal and is summarised in my private web area. )
If you combine that construction of Turaev's with the ideas of Moore and Segal then something very like what you are proposing seems to pop out. (I have not got yet to the point where I have written down the details for the Menagerie but it is slowly progressing in that direction (provided I can make sense of it all).
-
- CommentRowNumber95.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 15th 2010
- (edited Apr 15th 2010)
Tim, thanks for pointing our attention to your research proposal. that seems indeed to be quite related to what we are discussing here: looking forward for your contribution to this thread!
I’ll add a few details to what I was writing yesterday. the first one is purely algebraic (and well well well known): given a representation of a finite group on a vector space (on a characteristic zero field), the operator
is the projection on the subset of invariant vectors. so if V is 1-dimensional, this operator is either the identity (trivial representation) or zero (nontrivial representation). this remark should allow to think of “invariant sections” as a push-forward.
next, all we need here seems to be a natural flat bundle over the hom-spaces . in other words we have to associate an element in to a homotopy class of paths with fixed endpoints in . but this is straightforward: a single path in this class is an element in , with fixed boundary values; we transgress it to and then integrate over the whole homotopy class (see #91). that’s it.
-
- CommentRowNumber96.
- CommentAuthorUrs
- CommentTimeApr 15th 2010
Thanks, Domenico and Tim. Just in case you are wondering: I’ll be very busy with something else that I need to take care of. Will come back to the discussion here later.
-
- CommentRowNumber97.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 16th 2010
a very quick and short post, now; reconnecting later.
there’s a simple extended tqft pattern emerging here. we start with closed 3-manifolds, and we have closed 3-manifold —-> element in the abelian group U(1) then we generalize this to 3-manifolds with boundary to get 3-manifold with fixed boundary data –> element in U(1) this can be reread as 3-manifold with boundary –> {boundary data –> U(1)] or, even better 3-manifold with boundary –> matrix of U(1)-elements with indices corresponding to boundary data considering free U(1)-modules generated by boundary data, this finally becomes closed 2-manifold –> vector space; 3-manifold with boundary –> linear operator between the boundary vector spaces
the only step we need to make to go from numbers to vector spaces has been going from cohomology to relative cohomology. so the pattern should continue in a (in a sense) straightforward way: if we are able to associate a vector space to a closed 2-manifold, then we should also be able to associate a vector space to a 2-manifold with fixed boundary data. but then this should allow us to associate with a 2-manifold with boundary a “matrix of vector spaces”, which we could use as an operator between “vectors of vector spaces”, and the latter sould be nothing but Kapranov-Voevodsky 2-vector spaces.
-
- CommentRowNumber98.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 16th 2010
- (edited Apr 16th 2010)
I see the answer. it’s simple, it’s elegant, it’s completely abstract nonsense, it’s totally nPOV, and I absolutely do not exactly know what it means. in a word, it’s perfect :)
cohomology is a number (this should be read as “integrating a top degree cohomology class one gets a number” but “cohomology is a number” is a much more effective slogan :) ). relative cohomology is a linear operator (i.e., a morphism of vector spaces). relative relative cohomology is a 2-linear operator (a 2-morphism of 2-vector spaces). relative relative relative cohomology is a 3-linear operator. and so on.
so, in the DW model one should be able to describe the 3-linear operator associated with a 3-simplex, and that would encode the whole theory.
now we only need to go from nonsense to formal statements. to begin with: what is relative relative cohomology?
ok, I’ve dome my duty for today. now I can go and take a cappuccino, and then come back and read Urs post
created [[relative relative cohomology in a (oo,1)-topos]].
:)
-
- CommentRowNumber99.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 16th 2010
quite incredibly Urs has not been creating relative relative cohomology in an (oo,1)-topos, yet.. so it seems I’ll have to :)
here is my proposal: generalizing Urs idea for relative cohomology in an (oo,1)-topos from #86 above, relative relative cohomology in an (oo,1)-topos should be , where is the second oriental. and so on. this points to -nerves, but I have to think more carefully to this.
O Urs, Where Art Thou?
:)
-
- CommentRowNumber100.
- CommentAuthorUrs
- CommentTimeApr 16th 2010
Hi Domenico,
sorry, Thursdays and Fridays is our oo-category seminar-preparation and seminar days. I am entirely absorbed chatting infty cats here with Ieke. I’ll get back to you as soon as possible.