nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeApr 10th 2010
I was reading one of Mike’s papers on the way home and have some questions, but before I can ask those questions, I have an even simpler one…
Over on field there was some interesting discussion. I just drew some pictures.
What is the barrier keeping us from saying a field is simply an ∞-groupoid with one object with no non-identity n-morphisms for n>2?
Oh! I see. What you get is a ring (with inverse multiplication), but not a field because multiplication is not commutative. Is that right? So the barrier to a “clean” arrow theoretic definition of field is the commutative relation?
This would gel with some of my thoughts actually. Commutativity is often the result of some kind of limiting procedure, e.g. “continuum limit”. So if you take some kind of “continuum limit” of this 2-group, then I think you will get a field.
If I can take some liberty and call a 2-group a “noncommutative field”, then my gut tells me that a “commutative field”, i.e. just a field, is some kind of “continuum limit” of a noncommutative field.
-
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeApr 10th 2010
Hmm…
Actually, I think this “continuum limit” idea might have some merit. I think Urs has observed somewhere, and it made sense to me, that synthetic geometry, or nonstandard analysis, can be thought of as something along the lines of “continuum limit done right”.
Speculation: A field is a 2-group in which all morphisms are tangent morphisms.
A tangent morphism x is of the form
x=1+δxwhere δx is an infinitesimal morphism. The composition of any two infinitesimal morphisms is a morphism “0”.
Does that make any sense?
-
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeApr 10th 2010
An ∞-groupoid with one object and no nonidentity (>2)-morphisms is otherwise known as a 2-group. It has two kinds of things, 1-cells and 2-cells, with one operation on the 1-cells (composition) and two operations on the 2-cells (horizontal and vertical composition), which satisfy an interchange law. It’s not clear to me what this has to do with a field, or even a skew field (= “division ring” = “noncommutative field”), which has only one kind of thing, with two operations called addition and multiplication, which satisfy a distributive law, not an interchange law.
-
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeApr 10th 2010
Hi Mike,
I drew a diagram with one object, a bunch of arrows, and a bunch of 2-arrows.
I convinced myself that we can label morphisms by “times x” where x is an element of our ring, then composition of 1-morphisms is multiplication
x∘y↦xyand 2-morphisms represents “plus x” and with inverse “minus x”.
I am probably confused…
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeApr 10th 2010
Sorry, I can’t make sense of that yet. Are you saying that given a ring, you define a 2-group whose arrows and 2-arrows are both labeled by elements of the ring? What are the source and target of a 2-arrow?
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeApr 10th 2010
- (edited Apr 10th 2010)
Maybe Eric is approaching the statement that a ring is an Ab-enriched category with a single object and thinking of this with Ab identified with a subcategory of pointed one-object groupoids. The subtlety then is that in this enrichment the monoidal product on these groupoids in not the cartesian one (which would yield 2-groupoids in the enrichment) but the “bilinear one”, which does yield rings.
-
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeApr 10th 2010
- (edited Apr 10th 2010)
Is there a nice arrow theoretic way to describe symmetric monoidal categories? Whenever I see the definition of symmetric monoidal category, it makes me a little queasy.
Generally, am I asking too much to expect everything to have a nice arrow theoretic description? Somewhere in one of those long threads, I remember someone mentioning something about that confining me to enriched category theory, or something like that?
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeApr 10th 2010
If by arrow-theoretic you mean an description as internal to a such-and-such category, then for lots of things it is do-able. Symmetric monoidal categories can be written down internal to a category with finite limits, for example. I like internal stuff - it feels a bit like coordinate-free physics, in that you only refer to the whole shebang, not the individual points. There are no formulas, only commuting diagrams (well, ok, formulas expressing equalities of arrows).
However, if you don't mean internal-to-a-category, then I'm not sure I can help you.
Note that ordinary category theory is enriched, just enriched over Set with the cartesian product.
(must go to bed....)
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeApr 10th 2010
- (edited Apr 10th 2010)
@Eric: This is a hopeless endeavor. You have no chance ever of defining a field arrow theoretically, at least not in a useful way.
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeApr 10th 2010
Will someone please tell me what “arrow theoretic” means?!?
The category of fields is sketchable, which means that a field can be described as consisting of a certain shape of diagram (= functor) such that certain cones are limiting cones and certain cocones are colimiting cocones. And you only need finite limits and colimits, which means that you can define a notion of “field” internal to any category with finite limits and colimits. However, in that generality it probably won’t be a very useful notion.
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
@Mike good question - I've been assuming that it is either an internal construction, or completely using diagrams, as groups can be considered as a groupoid with one object. Other than that I'm in the dark :)
Edit: and it's cool that the category of fields is sketchable: do you have a reference?
-
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
David, it’s in Locally Presentable and Accessible Categories by Adamek and Rosicky, page 69, example 5. Much more generally, accessible categories are precisely equivalent to categories of models of so-called “basic” first-order theories (see their theorem 5.35 and surrounding discussion).
-
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Mike: Will someone please tell me what “arrow theoretic” means?!?
Asking me to define something clearly is an exercise in wishful thinking, but what I usually mean when I say “arrow theoretically” is that I can draw it. Or perhaps that it can be described (usually very simply) in terms of some basic category theoretic terms.
For example:
A group is a category with one object whose morphisms are all invertible.
That is an “arrow theoretic” statement.
An abelian group is a group satisfying xy=yx.
That is not an arrow theoretic statement since we had to use an equality, which is a foul, unless there is a clever way to state it in terms of commuting diagrams, which is allowed :)
However,
An abelian group is a 2-category with one object and one morphism whose 2-morphisms are all invertible.
That is an “arrow theoretic” statement.
Urs knows what I mean and can probably translate it to something clear enough.
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
Well Eric, it’s pretty easy to define an abelian group object in a category with finite products. It’s a group object (G,m:G×G→G,e:1→G) such that the following diagram commutes:
G×Gm→Gσ↓↓1GG×G→mGHere σ indicates a symmetry isomorphism which is definable in any category with products.
(I’m not sure why you have problems with the equation xy=yx, and not with the equation xx−1=e.)
-
- CommentRowNumber15.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Well Eric, it’s pretty easy to define an abelian group object in a category with finite products. It’s a group object (G,m:G×G→G,e:1→G) such that the following diagram commutes:
G×Gm→Gσ↓↓1GG×G→mGThat is exactly the kind of thing I try to avoid and wouldn’t consider that an “arrow theoretic” description. It is what makes me queasy when I see definitions of symmetric monoidal category. There should be some magic wand you can wave and all those diagrams fall out magically.
(I’m not sure why you have problems with the equation xy=yx, and not with the equation xx−1=e.)
Good point! I thought of that as I wrote it. I don’t have a good answer. I wish there was some way to say something along the lines of “A group is an ∞-modoid in which every 2-diagram 2-commutes”. Or something…
Then “An abelian group is an ∞-monoid with one object, one morphism and every 3-diagram 3-commutes.” Or something…
Those would be pure arrow theoretic statements. You’re right. The statement in terms of inverses is not purely arrow theoretic.
-
- CommentRowNumber16.
- CommentAuthorMike Shulman
- CommentTimeApr 11th 2010
I still have no idea what “arrow theoretic” means. @Eric #13, you do realize that saying that a diagram commutes is exactly the same as saying that two things are equal, right? (Namely, the two composites of parallel paths – or perhaps more, if it is a more complicated diagram.) If “arrow theoretic” means that you can draw it with commutative diagrams, then Todd’s #14 is arrow theoretic. If “arrow theoretic” means that it can be identified with some particular kind of n-category, then unfortunately (or fortunately) there are going to be lots of important and interesting concepts that are not arrow-theoretic.
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
Eric #15: is it the symmetry map σ that is source of the queasiness?
I am pretty much in the dark about “arrow-theoretic” as everyone else, but let me ask: is the notion of cartesian monoidal category (category with products) “arrow-theoretic” according to you?
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
@Mike: Todd's defintion is arrow theoretic in the way I was talking about. I'm pretty sure we can't define a field like that, because it doesn't seem like we can show 0 \neq 1 with a commutative diagram.
@Eric: It seems like you are trying to get rid of algebra, which is kinda sad. Algebra is a beautiful subject in its own right, but it is also the core of ordinary category theory. Your efforts offend my sensibilities. Please learn to love algebra instead of trying to kill it at every turn.
-
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeApr 11th 2010
Okay, I note that Todd’s definition consists not just of commutative diagrams, but also contains cartesian products, so those are part of “arrow theory a la Harry.” I presume that this extends to finite limits as well, so that for instance the definition of internal category is arrow theoretic a la Harry? And perhaps the models for any limit sketch? But if limit sketches are arrow theoretic, then I don’t see why limit-colimit sketches would be any less arrow-theoretic, and fields are the models of one of those.
-
- CommentRowNumber20.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
Are these “arrow-theoretic”?
“A braided monoidal category is a pseudomonoid in the monoidal 2-category of monoidal categories.”
“A symmetric monoidal category is a pseudomonoid in the monoidal 2-category of braided monoidal categories.”
“A category with products is a category where any diagonal functor into one of its finite powers has a right adjoint.”
My working hypothesis is that “arrow-theoretic” is not something one can make formally precise, but means something that you can describe in pure conceptual terms, never having to recite “unmotivated” equational axioms, or something like that. Sort of analogous to, “Love means never having to say you’re sorry.”
-
- CommentRowNumber21.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Todd: That sounds about right to me :D
Urs might have a better answer. I’m pretty sure he knows what I mean because whenever I ask for an “arrow theoretic” definition, if it exists, he can usually give me something that I consider “arrow theory”. In fact, that is probably the best definition. An arrow theoretic explanation is what Urs gives when I ask for an arrow theoretic explanation :)
For some reason, I doubt you will find that satisfying :)
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
@Mike: I'm not really sure that I am reading that diagram correctly, but there is no zero map in the category of commutative rings (with 1) because 1 must map to 1, and since 1=0 in the 0 ring, this means that the only map 0->X is when X=0.
It's also not at all clear to me what we're taking the equalizer of. I mean, you've got a bunch of arrows without objects next to them.
-
- CommentRowNumber23.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
The diagram looks a little funny and should be fixed up, but as for the equalizer, I think the missing object in the middle is a terminal set 1 (the ’empty product’, ha ha), and the element ’1’ whose domain is the missing object denotes the multiplicative identity provided by the limit sketch for commutative rings. (Also, the subobject I↪F should be exhibited as a subobject of F, rather than of F×F.) In other words, the equalizer is the subobject of “reciprocal pairs” in F×F.
-
- CommentRowNumber24.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
It’s good enough for now, Eric, as long as Urs is alive. :-) Slightly more seriously, I think I get what you meant now.
But hey – I gave you an arrow-theoretic definition of symmetric monoidal category that you asked for. You forgot to thank me! :-D
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
Hey, Todd, question for you. In higher category theory, why does it matter whether or not the categories themselves are strict as long as we have a weak notion of a morphism of n-categories?
-
- CommentRowNumber26.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Todd: You can imagine. It’s Sunday. A rare day at home with the family. Attention is not 100% :) I’ll need to look at what you wrote, but I can certainly thank you in advance. “Thank you!” :)
-
- CommentRowNumber27.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
I think one short answer might be that, for example, not every tricategory is weakly equivalent to a strict 3-category. For example, it is not generally true that the fundamental 3-groupoid of a space is weakly equivalent to a strict 3-category. This point is discussed in the monograph by Gordon-Power-Street, Coherence of Tricategories.
-
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
Maybe the definition of weak isn't weak enough though?
-
- CommentRowNumber29.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
There is no notion of weak equivalence that I know of or even imagine that would make every tricategory weakly equivalent to a strict 3-category, and just on general sociological grounds (with smart guys like Street looking into the matter), I feel safe in betting that there just ain’t one. But let us know if you find otherwise! :-)
I might be able to give a better answer later, but it’s time I went to bed.
-
- CommentRowNumber30.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
Eric: enjoy day with family! This is what it’s all about. :-)
-
- CommentRowNumber31.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
@Todd: I was just thinking about how there are a lot of notions of an n-category, but very few notions of what constitutes an equivalence, at least for Batanin/Trimble/Leinster operadic-style n-cats (as far as I know. I'd be delighted to be wrong in this case =)).
-
- CommentRowNumber32.
- CommentAuthorMike Shulman
- CommentTimeApr 11th 2010
@Harry #22, the diagrams are taking place in sets, not in commutative rings (how can I make this clearer in the text?). The map labeled “0” means “the map which picks out the zero element of F”. Sorry that the diagram got messed up, something weird happened with unicode.
@Todd #20, that doesn’t really help me, because it just pushes the question off to the definition of “conceptual” and/or “motivated.” I find all of the “non-arrow-theoretic” definitions being exhibited to be perfectly well motivated and conceptually explained.
@Harry #31, there are two known ways to define an equivalence of those, which are more or less the same. First is the naive notion, according to which a functor is an equivalence iff it is essentially k-surjective for all k. In order to make sense of “essentially k-surjective” you need a notion of when a (k+1)-morphism in an n-category is an internal equivalence, but that can easily be defined. The problem with this is that you then need a notion of weak functor, since not every equivalence can be witnessed by a strict functor. But we now have at least Garner’s proposal for a notion of weak functor, which even compose strictly associatively, and are essentially “maps out of a cofibrant replacement.”
OTOH there is the FOLDS-style definition of equivalence, where you first define what is meant by an acyclic fibration = surjective equivalence, namely a functor which is literally k-surjective for all k (e.g. for n=1 this is literally surjective on objects, full, and faithful), and then define two objects to be equivalent if they are connected by a span of acyclic fibrations. Here it’s fine to let the functors be strict, essentially because we can choose the object in the middle to be cofibrant, which leads us back to it looking almost like the first definition: such a span can be considered as a “weak functor” in either direction, i.e. as a map from a cofibrant replacement of one category to the other one.
Maybe those two constitute “very few,” but I think it’s pretty certain that they’re the “right” notion, so why do we need more? (-:
@Todd #29, there is of course at least one “notion of weak equivalence” which makes every tricategory weakly equivalent to a strict 3-category, namely the one in which every tricategory is weakly equivalent to every other tricategory. (-:O One argument that the existing notion is the “correct” one (and thus we shouldn’t be looking for weaker ones) is that it reduces to the known notion of equivalence for things like braided monoidal categories (as doubly degenerate tricategories) and homotopy 3-types (as tri-groupoids). Another is that it’s precisely what you get from the two general recipes I mentioned above.
-
- CommentRowNumber33.
- CommentAuthorMike Shulman
- CommentTimeApr 11th 2010
I wonder whether this discussion about “arrow theory” is symptomatic of why some people say that it is dangerous to learn too much category theory before you know enough of the rest of mathematics. Namely, because some things in category theory can be defined in clever ways and some theorems in category theory are proven by expanding definitions, you may start to believe (consciously or not) that everything in mathematics should be that way.
-
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
I haven’t been following this discussion here, but what Mike just said reminded me of what I tried to get across in our discussion with Eric about functors and adjunctions:. it is good to try to find slick category-theoretic definitions. But it leads nowhere particularly if you don’t first have a clean understanding of the plain definition itself.
But if you tell me what it is you are after, I can try to see what the answer might be.
-
- CommentRowNumber35.
- CommentAuthorEric
- CommentTimeApr 11th 2010
I can’t say anything about what a maths student should do, but in my experience the parts of category that have clever definitions tend to be those parts that are particularly applicable to physics. So I would have no hesitation suggesting that a physics student jump right into category theory as early as possible. However, it is conceivable that such an action could introduce a bias for a pure maths student, I think that bias would only benefit a physics student. I’m pretty sure that Kantization can someday be presented in a very elementary way that could eventually find itself into undergrad physics courses.
-
- CommentRowNumber36.
- CommentAuthorEric
- CommentTimeApr 11th 2010
But it leads nowhere particularly if you don’t first have a clean understanding of the plain definition itself.
I would say that a little differently. I would say
But it leads nowhere particularly if you don’t also have a clean understanding of the plain definition.
I don’t think the order of events matter. The only thing that matters is that you end up with a clean understanding of the plain definition. Whether or not the slick definition helps you get there doesn’t matter. In my case, the slick definitions are crucial for me to get there because I need pictures.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
All right, so what exactly is it you want to understand here?
-
- CommentRowNumber38.
- CommentAuthorEric
- CommentTimeApr 11th 2010
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeApr 11th 2010
I was hoping to find a nice clever arrow theoretic way to define field. But based on your comments in the discussion at field, I am not very optimistic.
Personally, I have come to think that maybe the notion of “field” is more an “accidental” property that a ring may have, than something of deep abstract meaning.
Abelian group, ring and module, these are deep abstract concepts. Some rings happen to be fields. Their modules then are called vector spaces. In the grand scheme of things, this does not seem to be as important as the concept of ring and module in general.
i might be wrong, though.
-
- CommentRowNumber40.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Thanks. That sounds reasonable to me too.
-
- CommentRowNumber41.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
@Mike #32, as I say, my hypothesis for what “arrow-theoretic” means for Eric was not something that can be defined or made formally precise; it was just a rough general idea of the type of thing he is looking for when he asks for an arrow-theoretic formulation, so that one can make a rough guess as to how to pitch a response.
Eric, one definition of field (in classical logic) might be this: a commutative ring R such that the poset of R-submodules of R consists of just the top and bottom R and {0}. Is that more satisfactory for you?
-
- CommentRowNumber42.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I feel like Eric is going to look up the word "module" at module, which is a really awful idea. Isn't the nLab's definition of a module something that is hopelessly complex if you don't understand what a module over a ring is?
Edit: Just as I suspected.
Eric, please skip the nLab definition and read about it on wikipedia. If you read the nLab definition, I can guarantee that you will miss the point.
-
- CommentRowNumber43.
- CommentAuthorEric
- CommentTimeApr 12th 2010
@Harry #42: I know the definition of a module, but I’m interested in knowing what you think “the point” is. I typically think of a module as a “generalized vector space”. Instead of being over a field, it is over a ring. Is there more to it? I also know “a” definition of bimodule and use them all the time, but I think there is a deeper “point” to bimodules I haven’t appreciated yet.
-
- CommentRowNumber44.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
Nope! A module is an abelian group with an R-action. Thinking about them as vector spaces will make you forget that most modules are not free and therefore do not admit bases.
-
- CommentRowNumber45.
- CommentAuthorTodd_Trimble
- CommentTimeApr 12th 2010
Of course, describing it as an abelian group with an R-action is question-begging. I know you know what you’re talking about, but how do you know Eric doesn’t know what he’s talking about? In this case, I think he does, because we’ve discussed such matters before!
I’m pretty sure Eric meant that just as a vector space over a field F can be regarded as an abelian group A equipped with a ring homomorphism F→hom(A,A), so a module over a ring R can be regarded as an abelian group A equipped with a ring homomorphism R→hom(A,A).
Why do you insinuate he didn’t know this?
-
- CommentRowNumber46.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
Because he started a thread asking a question about fields and abelian groups.
-
- CommentRowNumber47.
- CommentAuthorTodd_Trimble
- CommentTimeApr 12th 2010
Yes, but obviously he’s experimenting with ideas. It doesn’t mean he doesn’t know standard definitions of abelian group, field, and module!!!
The insinuation is presumptuous, and the tone condescending. Be nice.
-
- CommentRowNumber48.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
He keeps coming up with definitions that don't make sense! There's a huge difference between enrichment in abelian groups and enrichment in (effectively) categories. I disagree that there is any benefit to learning arrow-theoretic definitons first. If you tried to learn what a group was by studying the diagrams describing what a group is, you would not understand the definition of a group! Just looking at the diagrams, all groups look the same!
-
- CommentRowNumber49.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
And this is how research proceeds: by something not quite making sense and working on it until it does, discovering new things in the process.
One day you'll get to a point, Harry, where you're inventing mathematics, and then people will complain that your work doesn't make sense. It is at this point that the skills of patient explanation learned here will come in handy :)
-
- CommentRowNumber50.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
you would not understand the definition of a group!
the definition?? So some definitions are more equal than others?
Also, just by looking at the definition of a group using elements of a group then all groups look the same.
But by now I'm just pulling your leg, and I must stop. :) It's not very productive here or for work in the 'real world'.
-
- CommentRowNumber51.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
One day you'll get to a point, Harry, where you're inventing mathematics, and then people will complain that your work doesn't make sense. It is at this point that the skills of patient explanation learned here will come in handy :)
You don't invent mathematics. You discover mathematics. Invented mathematics is sterile and pointless, and I don't understand why we keep engaging in it here on the nForum.
That's not to say that all of the definitions of a higher category are worthless, however. There are real reasons to study higher categories, and there is no definition that captures every important point. That is why people are coming up with definitions and trying to "invent" higher categories. They're really trying to discover the right definition. Anyone who argues that there is a deficiency in the definition of a field is at best being an unserious researcher.
Contrast that with what we're doing here. Trying to come up with new definitions of a functor is not research, etc. There are real issues with other articles on the site, and we're sitting here talking about what color to paint the bike shed.
-
- CommentRowNumber52.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
Or uncovering new mathematics, if you like, the choice of phrase is immaterial. So is anyone who argues the deficiency of the current approach, while accepting that it is reasonable and gives the right answers, an unserious researcher? I don't think Eric is complaining about the definition of a field (Toby might do so, and the constructive definitions of a field here on the nlab are a result of various people doing so), but looking at another way to capture the properties of a field. The question is quite probably misguided for deeper theoretical reasons, but that is why he asked, and got several answers about non-algebricity of the category of fields and so on.
-
- CommentRowNumber53.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
Trying to come up with new definitions of a functor is not research, etc
I agree (edit: sort of..), but I was talking about you (Harry) in some hypothetical future endeavour, not Eric :)
But then what about coming up with a new definition of category? Toby looks at things like that (as well as new definitions of functors as a result). Or coming up with a new definition of manifold (and generalisations, I might add) as Urs and Andrew (for example) are wont to do. What about coming up with a new definition of algebraic variety? It was obvious what an algebraic variety was, and then people (Grothendieck, most famously) got inside and played around with it. Generalising Betti and torson numbers to homology groups? Emmy Noether must have been crazy!
There may not be much room in the definition of functor to wiggle, but it does us good to think hard about even the most basic of definitions now and then, I'm sure.
-
- CommentRowNumber54.
- CommentAuthorEric
- CommentTimeApr 12th 2010
By the way, these variations of standard definitions are part of my research. Everything I do has one single goal in mind. Understanding the fundamental nature of spacetime. I feel like the paper I wrote with Urs is a step in the right direction, but it is not “beautiful” enough (yet). I’m trying to find a beautiful way to express the ideas we talked about. Commutative diagrams and nondecomposable morphisms play an important part in that so I’m very happy that through the discussion here we came up with a slick unbiased definition of functor. Is it research? That depends on perspective I think. From a mathematicians perspective, I would completely understand if the answer was “no”. From a philosphical perspective? Maybe. From an ontological perspective? Maybe.
The process helped me and I suspect will help future students, so the effort was worth it in my opinion.
-
- CommentRowNumber55.
- CommentAuthorTodd_Trimble
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I strenuously disagree with a lot of # 51 on a lot of levels, so much so that it would take a long time to detail why. I’ll confine myself to just a few comments.
(1) It’s not the least bit clear that there is one “right” definition of higher category. A blanket assertion of that is sheer dogma. Believe it if you wish. I don’t.
(2) Nor is there one “right” way of doing and learning mathematics. Fine, so playing around with definitions of “functor” isn’t cutting-edge research. Does Eric pretend it is? No. But it’s his way of doing and learning, and that’s fine. We’re here to help. If you don’t like his experimenting around, then ignore it.
(3) If there are real issues with articles (as opposed to things to jeer at), then please bring them up. That is a great way to make valuable contributions.
-
- CommentRowNumber56.
- CommentAuthorEric
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
I agree with (2) which seems to contradict what I said just seconds before :)
I think finding an unbiased definition of functor is not mathematics research, but I do think it will ultimately help me with my research, so I count it losely as “research”. It was something “different” (yet equivalent) that hadn’t been expressed in words before that I think will help me push the envelope of my research. To be clear, I don’t think the new definition of functor is deep or even interesting to experts, but it is interesting to me.
PS: Of the variation we came up with, I actually think I like Harry’s the most. “A functor is a structure preserving map between categories.” In fact, that is probably a general definition encompassing lots of stuff. “A natural transformation is a structure preserving map between functors.” Then it is a matter of defining what “structure” means.
-
- CommentRowNumber57.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
@Todd:
1.) That is fair, but every definition of a higher category that I have seen is an attempt to rectify issues with other definitions. This is one of the interesting things that Lurie does in HTT. He works primarily with three different definitions of an (infinity,1)-category, and by showing that they are equivalent, is able to avoid the difficulties with working with quasicategories by passing to simplicial categories, etc. It may be that there is not even one clear definition of an (infinity,1)-category that captures all of these properties in a way that doesn't require an excess of theorems and proofs to show that everything works out nicely, but if such a definition were found, I can say with a reasonable amount of certainty that it would be adopted over all other formalisms.
2.) Eric just said that it was part of his research =.
3.) I wasn't jeering. I was just pointing it out. I haven't had time to edit much this year, but I intend to write a lot of stuff starting in a few weeks. One major problem that I see is when the "Idea" or "Motivation" section gets too long and makes it harder to find the formal definition. I'd also like to add in things like examples of computations, proofs, theorems, etc. I really like the way Joyal has structured his CatLab, and although I'm not nearly as familiar with the material as he is, I believe that I could make a big step towards bringing the level of rigour over here much closer to the level of rigour over there.
@Eric:
Bourbaki has a definition of structure. The definition I gave of a functor back when we were arguing about the free/forgetful adjunction is precisely the definition of a structure preserving map in the sense of Bourbaki. For example, it restricts to a homomorphism of monoids on endomorphism monoids. A very interesting way of thinking about categories is that they are the horizontalification of a monoid! Then a functor is the horizontalification of a homomorphism! In fact, if you read Bourbaki's Algebra, you can see that they define what it means for an association to be functorial without ever even defining a category or a commutative diagram. It is an algebraic idea!
-
- CommentRowNumber58.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
It is an algebraic idea!
meaning, it can be expressed as an algebraic idea - but not exclusively! (well, depending on what you mean by algebraic: topological spaces are famously "just" relational
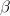 -modules, but try telling a topologist that all they are doing is algebra... 0:-)
-modules, but try telling a topologist that all they are doing is algebra... 0:-) -
- CommentRowNumber59.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
Functoriality is manifestly algebraic.
-
- CommentRowNumber60.
- CommentAuthorDavidRoberts
- CommentTimeApr 12th 2010
Just a little advocatus diaboli :)
-
- CommentRowNumber61.
- CommentAuthorTodd_Trimble
- CommentTimeApr 12th 2010
Harry #57: yes, your response to (3) is the kind of thing I’m talking about. Please point out specific articles where you think the Idea section is too verbose, and we can have a look. BTW: I too would like (in fact, love) to see more computations and proofs, provided they don’t get too long to include on a page. Separate pages for layered details of things like proofs is something that’s been brought up before (a “zoomable” approach to mathematics, to echo the way Mike put it).
I’d like to see what examples you have in mind with this. Are you helping Joyal over there? I haven’t been over there in a while.
-
- CommentRowNumber62.
- CommentAuthorHarry Gindi
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
Nope, but he's been writing it slowly but surely, and it's getting pretty substantial. He's probably written like 30-40 pages LaTeX-wise of mathematics, not counting the historical and biographical stuff.
I have nothing in mind yet, but my semester is over in a little over two weeks, so I intend to put some time into it then.
-
- CommentRowNumber63.
- CommentAuthorMike Shulman
- CommentTimeApr 12th 2010
@Eric #35 (previous page), note that in #33 I said (emphasis changed):
because some things in category theory can be defined in clever ways… you may start to believe (consciously or not) that everything in mathematics should be that way.
One might even go so far as to say that most things in category theory have clever definitions. But my point was that outside of category theory, clever definitions are the exception rather than the rule. In particular, the mathematical concept of “field” is not really part of category theory (though we can use category theory to study it, as we can with most of mathematics), and so there is no reason to expect it to have a clever definition.
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeSep 1st 2012
I have re-organized field a little, and have added list of pointers to examples and to related concepts.
Also, hereby I am moving an old discussion that used to sit there to here:
[ begin forwarded discussion ]
Discussion
This discussion was originally at vector space, but most of it is really about fields.
Eric Forgy says: Is there a nice arrow theoretic way to define vector spaces?
Urs says: There is comparatively nice abstract nonsense to be said about rings. For instance, a ring is a category with one object enriched in the category of abelian groups. From that starting point the concepts of ring theory develop rather naturally from pure category theoretic reasoning. In particular modules over rings appear naturally.
For some reason this is different when rings are refined to fields and modules to vector spaces. The very concept of a field is somehow not as natural from a category theoretic perspective, or at least I don’t see how it is. This problem becomes very manifest when one tries to categorify fields and vector spaces: it is very straightforward to categorify rings and their modules, but their refinement to categorified fields and vector spaces is harder.
Eric says: Well, fields are closely tied to the continuum and we know the continuum is not natural :)
Toby says: *tongue where it belongs* A field may be defined a ring that has been decomposed (as a set) as the sum of a point and a group, with the point being the zero element and the the group being a multiplicative submonoid. However, this definition does not work in constructive analysis; one cannot prove constructively that the ring of real numbers has this property. Instead, one must define a field to be a ring equipped with an apartness relation satisfying some properties (which I can write down if desired). Classically, an apartness relation is a vacuous structure, but in constructive mathematics its properties have a very topological flavour, even though it's much simpler than a topology. All of the deep issues about the continuum are already there in the constructivists' notion of apartness, which they require to even define what a field is.
John says: As Toby notes, fields are a somewhat awkward concept in constructive mathematics. The basic problem is that their definition involves a clause “if x≠0, then x has an inverse…” A clause of the for “if something is not true, then…” is rather annoying in constructive mathematics. This means fields are not very nice if you’re trying to do math in an arbitrary topos. And since topos theory was invented when Grothendieck was working on algebraic geometry, this should mean that fields are not very nice when you’re trying to do algebraic geometry!
Of course this is a bit shocking, since the first thing an elementary text on algebraic geometry does is say “Let k be a field.” But Grothendieck’s revolutionary approach to algebraic geometry also downplays the importance of fields, so presumably it all hangs together once you understand it.
I wish I understood this better. There’s a nice exposition of a little bit of these ideas in Mac Lane and Moerdijk’s Sheaves in Geometry and Logic: A First Introduction to Topos Theory. Look up ’local ring’ in their index: you’ll see that unlike the notion of field, the notion of local ring can be defined using ’geometric logic’, which is (very roughly) the kind of logic that works well in topoi.
Eric says: The wikipedia article on Category of fields has some interesting things to say about the difficulties with fields in category theory.
If fields are less than perfectly natural, then vector spaces are somewhat troublesome too. But what about the tangent bundle of a category? That idea is very pretty. In what way does it fail to converge to the usual concept of a tangent space, which should contain vector spaces (obviously)?
Toby says: Rather than think about the category of fields, shouldn't we think of fields as nice objects in the nice category of rings? Modules, after all, behave beautifully.
John says: Unlike the category of fields, the category of vector spaces is not troublesome at all! But there’s no contradiction here. When Eric wrote “fields are less than perfectly natural”, he was being a bit vague. Fields are wonderfully well-behaved rings, and rings form a wonderfully well-behaved category. But the category of fields is not so nice. As Toby notes, this is completely typical. So, if we fix a field and take the category of vector spaces over it, that category is wonderfully nice.
I have a question. This article says the category of fields is ’accessible’, and it says that an accessible category is the category of models of a sketch. What sort of sketch does the job for fields. They’re not models of a finite limits theory, so I assume we also need some colimits in our sketch. How does this work? Which constructive definition(s) of field do we use?
Gonçalo Marques: The sketch for fields is described on page 248 of “Category theory for computing science” by Michael Barr and Charles Wells (3rd edition). They use what they call “finite discrete sketches”. It does involve a cocone.
[ end forwarded discussion ]
-
- CommentRowNumber65.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
So glad you’re cleaning up entries, Urs. Less of a sandbox feel.
-
- CommentRowNumber66.
- CommentAuthorUrs
- CommentTimeSep 1st 2012
- (edited Sep 1st 2012)
Yes, I think one can see a certain evolution in how nLab entries are being written. Lots of the entries that were written when the Lab was still young are rather messy. It seems it took all of us a while to get a feel for how to write mathematical text on a wiki.
These days I am trying to use formal Definition/Remark/Theorem/Proof-environments a lot. It may feel a bit pedantic at times, but it enforces a certain organization that helps not only the reader, but also the authors.
-
- CommentRowNumber67.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
These days I am trying to use formal Definition/Remark/Theorem/Proof-environments a lot. It may feel a bit pedantic at times, but it enforces a certain organization that helps not only the reader, but also the authors.
I agree 100%, and I tend to do the same. It structures things better, and it’s less stream-of-consciousness. (And I love details, details, details. Since all my work is done from home without benefit of face-to-face, I get easily confused unless there’s lots of detail in definitions and proofs.)
-
- CommentRowNumber68.
- CommentAuthorTobyBartels
- CommentTimeSep 1st 2012
- (edited Sep 1st 2012)
I put the constructive definitions under Definitions, put definitions into definition environments, and reworded some things.
-
- CommentRowNumber69.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
Lots of the entries that were written when the Lab was still young are rather messy.
That’s especially true in some of the older uses made of query boxes, which prompts me to make this comment: it seems to me now that query boxes can serve an excellent purpose when used to sound a warning or point out potential confusion which is pending fuller address and rectification, but not as good for long discussions at more of a beginner-level. The nForum is really the place to hash out long discussions (and pointers to query boxes should always be made at the nForum, otherwise they tend to languish). I suppose this might be obvious, but only so after some evolution.
-
- CommentRowNumber70.
- CommentAuthorMike Shulman
- CommentTimeSep 1st 2012
Definition/Theorem/etc. environments are great, but I think in general we should try to avoid putting anything in them that is longer than one paragraph, with maybe one displayed equation or a couple of bullet points. (The exception is Proof environments, of course.) I find that a good deal of the value provided by such structure is lost when the statements become very long and take up most of my computer screen, so I can’t place them in context visually. Plus, in Definition environments that are in ordinary font, instiki (unlike latex) makes it hard to tell where the end of such an environment is.
-
- CommentRowNumber71.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
Definition/Theorem/etc. environments are great, but I think in general we should try to avoid putting anything in them that is longer than one paragraph, with maybe one displayed equation or a couple of bullet points.
I agree that seems like a good rule of thumb.
-
- CommentRowNumber72.
- CommentAuthorTobyBartels
- CommentTimeSep 1st 2012
We could change the font of Definition environments (and Remark and Example environments) if we wanted to. (I do generally agree with Mike.)
-
- CommentRowNumber73.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
I actually like the font for definition and theorem environments (un-italicized) more than I do for proposition environments, because the italics make displayed math look tilted and askew.
-
- CommentRowNumber74.
- CommentAuthorTobyBartels
- CommentTimeSep 1st 2012
We can change them all! (Specific proposals, of course, need to go in a separate thread to be adopted.)
-
- CommentRowNumber75.
- CommentAuthorMike Shulman
- CommentTimeSep 2nd 2012
@Todd 73: Agreed. What would be ideal, though, would be if the italics could somehow be not applied to math, only to text. (Can CSS be that smart?) Then I would support making more things italic.
-
- CommentRowNumber76.
- CommentAuthorTobyBartels
- CommentTimeSep 2nd 2012
I’m putting this italics stuff in a too broadly named separate thread.
1 to 76 of 76