nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeApr 30th 2010
added at adjoint functor
more details in the section In terms of universal arrows;
a bit in the section Examples
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 24th 2011)
While Lab is down I must write here some essential notes, which are actually of interest for discussion as well.
- Samuel Eilenberg, John C. Moore, Adjoint functors and triples, Illinois J. Math. 9, Issue 3 (1965), 381-398.
Here triple is unfortunately in the sense of monad. Section 3 is called Adjoint triples but is not what we call adjoint triples, but instead the case where the underlying endofunctor of a monad has a right adjoint . Then automatically is a part of a comonad where and are in some sense dual to and . Thus there is a correspondence between monads having right adjoint and comonads having left adjoint, what Rosenberg calls duality. I am not sure that the terminology is optimal. In any case, it is a little more than a consequence of two general facts.
If then for every natural number .
Given two adjunctions and where , then there is a bijection between the natural transformations and natural transformations such that
where the horizontal arrows are the natural bijections given by the adjunctions. If and are their unit and counit of course the upper arrow is and the lower arrow . Thus the condition renders as
or . Given , the uniqueness of is clear from the above diagram, as the horizontal arrows are invertible. determines , namely . For the existence of (given ) satisfying the above equation, one proposes that is the composition , i.e.
and checks that it works. The inverse is similarly given by the composition
The mechanism strongly reminds of mates, but it is not (classical) mates (in their case one starts with one adjunction). Maybe somebody can elucidate the connection, maybe in some framework it is the same.
This now enables in a special case to dualize to , and similarly unit to the counit. I guess one could do that kind of dualization for more general algebras over operads in the category of endofunctors. By the way, is this extension known ?
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 24th 2011)
No, above is the old form, the newest update has been lost in refresh.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 25th 2011)
While Lab is down I must write here some essential notes, which are actually of interest for discussion as well.
- Samuel Eilenberg, John C. Moore, Adjoint functors and triples, Illinois J. Math. 9, Issue 3 (1965), 381-398.
Here triple is unfortunately in the sense of monad. Section 3 is called Adjoint triples but is not what we call adjoint triples, but instead the case where the underlying endofunctor of a monad has a right adjoint . Then automatically is a part of a comonad where and are in some sense dual to and . Thus there is a correspondence between monads having right adjoint and comonads having left adjoint, what Rosenberg calls duality. I am not sure that the terminology is optimal. In any case, it is a little more than a consequence of two general facts.
If then for every natural number .
Given two adjunctions and where , then there is a bijection between the natural transformations and natural transformations such that
where the horizontal arrows are the natural bijections given by the adjunctions. If and are their unit and counit of course the upper arrow is and the lower arrow . Thus the condition renders as
or . Given , the uniqueness of is clear from the above diagram, as the horizontal arrows are invertible. determines , namely . For the existence of (given ) satisfying the above equation, one proposes that is the composition , i.e.
and checks that it works. The inverse is similarly given by the composition
The mechanism strongly reminds of mates, but it is not (classical) mates (in their case one starts with one adjunction). Maybe somebody can elucidate the connection, maybe in some framework it is the same.
This now enables in a special case to dualize to , and similarly unit to the counit. I guess one could do that kind of dualization for more general algebras over operads in the category of endofunctors. By the way, is this extension known ?
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 24th 2011)
Well now I got it correct in source code. Number 3. Except no formulas in the output!!
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
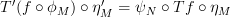
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
Strange 6 has a formula in double dollar sign in Markdown+Itex and it does not appear. 7 has the same formula as text output. Over there, the machine has changed the dollar signs into latex in brackets front and back and appeared as a formula. Is somebody experimenting ? -
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 24th 2011)
More experimenting
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
Urs’s formula
-
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber12.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber13.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- Eilenberg-Moore, euclid
-
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber15.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
- (edited Apr 24th 2011)
I am not getting it…
-
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber17.
- CommentAuthorzskoda
- CommentTimeApr 24th 2011
-
- CommentRowNumber18.
- CommentAuthorMike Shulman
- CommentTimeApr 25th 2011
I still cannot see the math in any of the above comments.
-
- CommentRowNumber19.
- CommentAuthorzskoda
- CommentTimeApr 25th 2011
- (edited Apr 25th 2011)
Let me try to reinput, that should rerender…I hope.
-
- CommentRowNumber20.
- CommentAuthorzskoda
- CommentTimeApr 25th 2011
- (edited Apr 25th 2011)
Yes, finally!
Edit: well no. I made some changes to 4 and some formulas now appeared but some did not.
-
- CommentRowNumber21.
- CommentAuthorzskoda
- CommentTimeApr 25th 2011
It is strange that the math code from my long comment 4 works when copied and pasted into adjoint monad (new entry announced here).
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeApr 26th 2011
As far as I can tell from what I can see, this is exactly the notion of mate, in the special case when the functors without adjoints are identities. What do you mean by “in their case one starts with one adjunction”?
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeApr 26th 2011
- (edited Apr 26th 2011)
Of course, I expected Mike to find the connection.
Hm, now I look into mate and there you indeed start with two adjunctions. I took the notion of mates from Leinster’s book math.CT/0305049 where he starts with one adjunction only, page 150 (180 of the file).
He starts with ONE adjunction , , and two functors , . Then there is a correspondence between the transformations and the transformations .
The Lab entry mate, as I now see, has two adjunctions and two 1-cells to start with. I did not see that general version. Thanks.
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMay 18th 2011
spelled out at adjoint functor in detail the basic proof that a right adjoint is faithful precisely if the counit has epi components.
-
- CommentRowNumber25.
- CommentAuthoreparejatobes
- CommentTimeMar 12th 2012
added at adjoint functor the definition in terms of extensions/liftings, plus when a right/left adjoint is full in terms of the counit/unit
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 12th 2012
Thanks.
For the sake of those readers who come across this and don’t (yet) know what “” stands for and who don’t (yet) know what “absolute” refers to, I have slightly edited to read as follows:
Given , we have that it has a right adjoint precisely if the left Kan extension of the identity along exists and is absolute, in which case .
What do you think?
-
- CommentRowNumber27.
- CommentAuthoreparejatobes
- CommentTimeMar 12th 2012
great, thanks. I was in a hurry and didn’t gave a lot of thought to the phrasing. It’s clearer now. I’ve also changed s for s.
Btw, is there a way to link to specific sections within a page? here for example, I’d rather have a link to a (to be added) section of Kan extension detailing when one such is absolute, than to absolute colimit
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeMar 12th 2012
is there a way to link to specific sections within a page?
Yes, but unfortunately not in a nice wiki-way.
You can link to any URl by writing
[follow this link](http://url.com/see/here.html)and this may of course include anchors, such as
[follow this link](http://url.com/see/here.html#anchor)So
[absolute Kan extensiuon](http://ncatlab.org/nlab/show/Kan+extension#AbsoluteKanExtension)produces the link that you want: absolute Kan extensiuon
(and see the source code of Kan extension for how I produced that anchor to that subsection).
-
- CommentRowNumber29.
- CommentAuthoreparejatobes
- CommentTimeMar 12th 2012
Ok, many thanks Urs
-
- CommentRowNumber30.
- CommentAuthorMike Shulman
- CommentTimeMar 12th 2012
BTW, you can leave off the “http://ncatlab.org” from the URL and it will still work (and even continue to work if the nLab’s domain name had to be changed).
-
- CommentRowNumber31.
- CommentAuthoreparejatobes
- CommentTimeMar 13th 2012
done! added a rel link to the absolute kan extension section
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeNov 28th 2014
added more historical references
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeJun 2nd 2018
I am trying to bring this page into better expositional shape. First, I have now rewritten and expanded, with full proofs, the section In terms of hom-isomorphisms.
-
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeJun 2nd 2018
I have also changed the Idea-section. Removed the would-be attempt at a definition, since that is now discussed in the main text. Then I added an absolute minimum of words to put the concept in perspective. Should be expanded. Could be expanded to a long conceptual section, optimally.
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeJun 3rd 2018
- (edited Jun 3rd 2018)
Now I have polished and expanded the next section: In terms of representable functors
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeJun 3rd 2018
now I have similarly touched the next section: In terms of universal factorization through a (co)unit
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeJun 3rd 2018
after the lead-in sentence claiming a key role of the concept of adjoint functors, I added this as a footnote:
“In all those areas where category theory is actively used the categorical concept of adjoint functor has come to play a key role.” (first line from An interview with William Lawvere, paraphrasing the first paragraph of Taking categories seriously)
-
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeJun 20th 2018
I have polished and expanded the discussion of left adjoints via pointwise limits over comma categories, now this Prop..
-
- CommentRowNumber39.
- CommentAuthorDavid_Corfield
- CommentTimeSep 2nd 2018
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeJan 28th 2019
- (edited Jan 28th 2019)
replaced the first occurence of an Instikiti
array-hack for adjoint pair notation by atikzcd-version\begin{center} \begin{tikzcd} \mathcal{D} \arrow[r, shift right=6pt, "R"', "\bot"] & \mathcal{C} \arrow[l, shift right=6pt, "L"'] \end{tikzcd} \end{center}Suggestions for improvements welcome.
What’s the
tikzcd-analog of what inxymatrixis\ar@{<-}[r]?
-
- CommentRowNumber41.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2019
\ar[r,<-]or\ar[from=r](I’m not actually sure if these is a difference between these) -
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeJan 29th 2019
Thanks!
I just wanted to add this to the HowTo here, as another escaped-code example, but it seesm that generally the parser gets confused when there is escaped tikz-code, so I am removing it again.
-
- CommentRowNumber43.
- CommentAuthorRichard Williamson
- CommentTimeJan 29th 2019
- (edited Jan 29th 2019)
Yes, currently the Tikz code cannot be escaped, either by a
<nowiki>block or in a code block. It is tricky to get this to work due to the interaction between the new and old renderer. I will try to fix it when I get the chance. In the meantime, one can always link to the source. -
- CommentRowNumber44.
- CommentAuthorRichard Williamson
- CommentTimeFeb 2nd 2019
The issues with escaping should now be fixed.
-
- CommentRowNumber45.
- CommentAuthornLab edit announcer
- CommentTimeJun 6th 2019
Fixes typo in diagram: the discussion that follows implies C should be the domain of the functor L and the codomain of the functor R, and not vice versa. There may be other similar typos in the remainder of the article, I haven’t done an exhaustive search (and am not good enough with LaTeX to be confident making extensive edits).
Asad
-
- CommentRowNumber46.
- CommentAuthorDavid_Corfield
- CommentTimeJun 7th 2019
-
- CommentRowNumber47.
- CommentAuthorDean
- CommentTimeNov 24th 2019
There is a certain lemma about adjoint functors that makes some of these things more manifest. See “Adjunctions” here https://edeany.com. Are people ok with me adding this lemma here?
-
- CommentRowNumber48.
- CommentAuthorTodd_Trimble
- CommentTimeNov 24th 2019
Not clear what lemma you’re talking about. You should probably just state your lemma here rather than getting people to copy and paste your address into a separate window and then read a bunch of stuff.
-
- CommentRowNumber49.
- CommentAuthorMike Shulman
- CommentTimeNov 25th 2019
If you write
<https://edeany.com>it will automatically be a link (https://edeany.com). -
- CommentRowNumber50.
- CommentAuthornLab edit announcer
- CommentTimeDec 23rd 2019
-
- CommentRowNumber51.
- CommentAuthornLab edit announcer
- CommentTimeDec 23rd 2019
-
- CommentRowNumber52.
- CommentAuthoraleks
- CommentTimeJun 2nd 2020
-
- CommentRowNumber53.
- CommentAuthoraleks
- CommentTimeJun 2nd 2020
-
- CommentRowNumber54.
- CommentAuthoraleks
- CommentTimeJun 2nd 2020
-
- CommentRowNumber55.
- CommentAuthorJohn Baez
- CommentTimeJun 23rd 2020
-
- CommentRowNumber56.
- CommentAuthorJohn Baez
- CommentTimeJun 23rd 2020
-
- CommentRowNumber57.
- CommentAuthorJas
- CommentTimeSep 12th 2020
Is there a typo in diagram (2) (the commutative square)? I don’t see how the vertical arrows are induced by and - I have read the definition of hom-functor. It works if is considered instead of , and same goes for other hom sets.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeSep 12th 2020
-
- CommentRowNumber59.
- CommentAuthorJ-B Vienney
- CommentTimeAug 14th 2022
- (edited Aug 14th 2022)
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeAug 14th 2022
- (edited Aug 14th 2022)
Thanks, this is good material (here).
In the first lines I have fixed an “” to “” and an “” to “”, since that’s what you are using in the following. (On the other hand, myself, I prefer “” for the generic pair of adjoints, for what I find are obvious reasons: e.g. it is not generally the case that an Underlying functor is a right adjoint.)
Then I took the liberty of removing the bullet item markup and replacing it by numeration by hand. This is a hack to workaround a shortcoming of the nLab software: Once you include
tikzcddiagrams in anInstikibullet item, Instiki gives up and ends the itemize typesetting. As a result, the left alignment in your text did not come out as intended.(At some point in the future we are going to hire a programmer to fix this and related software issues.)
-
- CommentRowNumber61.
- CommentAuthorHurkyl
- CommentTimeAug 14th 2022
- (edited Aug 14th 2022)
Huh. I’m surprised that indenting sections in the source doesn’t fix the “instiki gives up” issue. I guess this system works differently than others I’ve used. (or maybe I accidentally made a different error when trying this fix)
-
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeAug 14th 2022
- (edited Aug 14th 2022)
Yes, Instiki does not have markup for plain indentation. In fact, markup given by indenting by 6 or more whitespaces is interpreted differently altogether: it produces (indented, yes, but) verbatim output of the source.
-
- CommentRowNumber63.
- CommentAuthorvarkor
- CommentTimeDec 17th 2022
-
- CommentRowNumber64.
- CommentAuthorncfavier
- CommentTimeFeb 19th 2023
- (edited Feb 19th 2023)
Added composition of adjunctions (L’ ∘ L ⊣ R ∘ R’), precomposite adjunctions (— ∘ R ⊣ — ∘ L) and postcomposite adjunctions (L ∘ — ⊣ R ∘ —). Connected this to the fact that adjoints are absolute Kan extensions/lifts of the identity.
I couldn’t find this in the literature (but I didn’t look very hard), so if this is known under a different name, or if you have a reference, please add.
Formalisation of the pre/postcomposite adjunctions in Agda for the 1lab: https://github.com/plt-amy/1lab/pull/193/files#diff-b2e8196987b851f006e0efde215ecbf35f972e7eeee3ae3a1612cb4f8a480b61
-
- CommentRowNumber65.
- CommentAuthorUrs
- CommentTimeFeb 19th 2023
Thanks. If there is a good/stable link to the Agda formalization, then let’s add it to the entry.
-
- CommentRowNumber66.
- CommentAuthorncfavier
- CommentTimeFeb 19th 2023
Sure, I can add that once the pull request gets merged.
In general it would be nice to systematically have links from nlab pages to their formalised equivalents in projects like the cubical library, the 1lab, and/or agda-unimath.
-
- CommentRowNumber67.
- CommentAuthorUrs
- CommentTimeFeb 19th 2023
-
- CommentRowNumber68.
- CommentAuthorUrs
- CommentTimeMar 31st 2023
Prodded by discussion here I have added to the very top of this entry highlighting of the parallel entry adjunction.
-
- CommentRowNumber69.
- CommentAuthorUrs
- CommentTimeMay 5th 2023
added a section “Transformation of adjoints” (here) with currently (just) the least general (but maybe most important) version of the definition (MacLane’s “conjugate” transformations) with a brief comment on the relation to bifibrations.
Since this probably deserves an entry of its own, I will also copy these paragraphs to a new entry transformation of adjoints.
-
- CommentRowNumber70.
- CommentAuthorUrs
- CommentTimeMay 6th 2023
- (edited May 6th 2023)
I have moved the lead-in sentences out of the Definition-section into a new Idea-section (now here)
then expanded there a good bit, such as in making explicit the similarity to adjoint linear operators
and moved the Lawvere quote out of a footnote into a quote-environment
and added to it a paragraph quoted from p. 103 in MacLane71
-
- CommentRowNumber71.
- CommentAuthorvarkor
- CommentTimeMay 31st 2023
-
- CommentRowNumber72.
- CommentAuthorUrs
- CommentTimeMay 31st 2023
-
- CommentRowNumber73.
- CommentAuthornonemenon
- CommentTimeJun 27th 2023
-
- CommentRowNumber74.
- CommentAuthornonemenon
- CommentTimeJun 27th 2023
-
- CommentRowNumber75.
- CommentAuthornLab edit announcer
- CommentTimeJul 17th 2023
-
- CommentRowNumber76.
- CommentAuthorUrs
- CommentTimeAug 10th 2023
added another early historical reference:
- Peter J. Huber, §4 in: Homotopy theory in general categories, Mathematische Annalen 144 (1961) 361–385 [doi:10.1007/BF01396534]
1 to 76 of 76