Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: quaternionic oriented cohomology theory

Bottom of Page

1 to 14 of 14

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2020
    • (edited Dec 31st 2020)

    starting something. For the moment just checking what literature exists. So far I am aware of this:

    v1, current

    • CommentRowNumber2.
    • CommentAuthorDavid_Corfield
    • CommentTimeNov 25th 2020

    Just seeing what it is, I came across this PhD thesis by Craig Matthew Laughton, Quasitoric manifolds and cobordism theory. A definition at Example 2.2.5.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2020

    Thanks! I have added this as Laughton 08. Also at MSp.

    diff, v2, current

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2020

    added the obstruction-theoretic argument for the existence of quaternionic orientations (here) together with the conclusion that KOKO is quaternionic orientable (here)

    diff, v2, current

    • CommentRowNumber5.
    • CommentAuthorDavid_Corfield
    • CommentTimeNov 25th 2020

    There’s also the example

    Among quaternionic oriented cohomology theories, quaternionic cobordism is universal in the analogous fashion to complex cobordism (Laughton, Example 2.2.9)

    • CommentRowNumber6.
    • CommentAuthorDavid_Corfield
    • CommentTimeNov 25th 2020

    I’ll add that, but it should be said more precisely.

    diff, v3, current

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2020
    • (edited Nov 25th 2020)

    I made quaternionic cobordism redirect to MSp

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeDec 31st 2020
    • (edited Dec 31st 2020)

    Implicit (?) in Baker 92 is the suggestion that we get a quaternionic orientation 12p 1 E\tfrac{1}{2}p_1^E from the second Conner-Floyd Chern class c 2 Ec_2^E of any complex orientation c 1 Ec_1^E, by defining it via the solid triangle here:

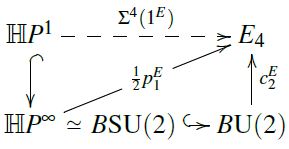
    It remains to see that this really satisfies the defining condition, hence that the dashed morphism makes the top triangle homotopy-commute.

    To that end I am looking at the following solid diagram:

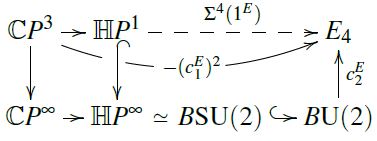
    That makes it rather plausible. But I am still looking for a formal way to prove it.

    • CommentRowNumber9.
    • CommentAuthorDylan Wilson
    • CommentTimeDec 31st 2020
    @Urs, (c_1^E)^2 is zero when restricted to CP^2, so it factors through CP^3/CP^2 = HP^1 as indicated
    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeDec 31st 2020
    • (edited Jan 21st 2021)

    Thanks, Dylan! I had just seen it myself and was typing it up:

    [edit on 21st Jan 2021: image removed]

    [edit on 21st Jan 2021: Hm, no, this argument is wrong. For instance, it would imply that all degree-6 cohomology of ℂP 3\mathbb{C}P^3 comes pulled back from S 4S^4, which is nonsense. I guess the problem is that the square (b) is not actually a homotopy pushout. It seems to be from the pasting law applied to its pasting with (c), but that needs an argument that the homotopies filling these squares match up, and that might fail.]

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeDec 31st 2020
    • (edited Jan 21st 2021)

    [removed]

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeDec 31st 2020

    Next, I’d like to refine this statement to finite-stage orientations:

    It ought to be true that a quaternionic orientation “at stage nn”, i.e. an extension of this form:

    ℍP 1 ⟶Σ 4(1 E) E 4 ↓ ↗ 12p 1 E ℍP n \array{ \mathbb{H}P^1 &\overset{\Sigma^4(1^E)}{\longrightarrow}& E_4 \\ \big\downarrow & \nearrow_{\mathrlap{ \tfrac{1}{2}p_1^E }} \\ \mathbb{H}P^n }

    may analogously be induced from a complex orientation at stage 2n+12n + 1, i.e. from an extension of this form

    ℂP 1 ⟶Σ 2(1 E) E 2 ↓ ↗ c 1 E ℂP 2n+1 \array{ \mathbb{C}P^1 &\overset{\Sigma^2(1^E)}{\longrightarrow}& E_2 \\ \big\downarrow & \nearrow_{\mathrlap{ c_1^E }} \\ \mathbb{C}P^{2n+1} }

    By adapting the above proof and using the construction of the Conner-Floyd classes here, this should be implied from observing that the canonical map

    ℂP 2n+1⟶ℍP n \mathbb{C}P^{2n+1} \longrightarrow \mathbb{H}P^n

    is in fact the complex projective bundle of the canonical quaternionic line bundle on ℍP n\mathbb{H}P^n.

    This ought to be true (e.g. the fiber is ℂP 1\mathbb{C}P^1, as it should be for the projective bundle of a rank-2 complex vector bundle), but I still need to write a formal proof.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeJan 3rd 2021

    added this pointer:

    diff, v8, current

    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2021
    • (edited Jan 24th 2021)

    The argument in #9, #10 above was not correct (for instance: the same argument would immediately imply that ℂP 3\mathbb{C}P^3 has no ordinary cohomolgy in degree 6…).

    The following argument should work. It’s essentially a standard basic argument in complex oriented cohomology theory, and I suppose I am making a fool of myself here in going on about this at all. But here goes:

    To recall, the question was:

    How to formally show that every complex orientation c 1 Ec^E_1 induces a quaternionic orientation by setting 12p 1 E≔c 2 E\tfrac{1}{2}p^E_1 \;\coloneqq\; c^E_2?

    First, a quick abstract way to see it:

    Just as complex orientations are co-represented by the ring spectrum MUMU (all homotopy-commutative), so quaternionic orientations are co-represented by the ring spectrum MSpMSp (by the same proof, just with the evident substitutions), and the evident map MSp⟶MUMSp \longrightarrow MU is a ring spectrum homomorphisms. This way complex orientations MU→EMU \to E immediately induce quaternionic representations MSp→EMSp \to E by precomposition with MSp→MUMSp \to MU.

    Unravelling this, what is happening under the hood:

    1. Under the equivalence ℍP ∞≃Th(ℒ ℍP ∞ *)\mathbb{H}P^\infty \simeq Th\big( \mathcal{L}^\ast_{\mathbb{H}P^\infty} \big) the following two inclusions are equivalent (by this diagram):

      1. the canonical inclusion S 4≃ℍP 1↪ℍP ∞S^4 \simeq \mathbb{H}P^1 \hookrightarrow \mathbb{H}P^\infty;

      2. the canonical inclusion S 4≃Th(ℍ)↪Th(ℒ ℍP ∞ *)S^4 \simeq Th\big( \mathbb{H} \big) \hookrightarrow Th\big( \mathcal{L}^\ast_{\mathbb{H}P^\infty} \big).

    2. The fact that the Conner-Floyd Chern class c 2 Ec^E_2 is a Thom class for complex rank-2 bundles says it restricts to unity along the second of these maps.

    But by the equivalence to the first of these maps, it also restricts to unity there, and this was to be shown.

    Of course the very same argument run in reverse shows that c 1 Ec^E_1 itself really gives an orientation of complex line bundles. So, nothing to see here, please move along.

1 to 14 of 14

  1.