Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: microlinear space

Bottom of Page

1 to 12 of 12

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    created microlinear space

    One thing I might be mixed up above:

    in the literature I have seen it seems to say that

    $ X^D x_X X^D \simeq X^{D(2)}$

    with

    $ D(2) = { (x_1,x_2) \in R \times R | x_i x_j = 0} $.

    But shouldn't it be

    $ D(2)' = { (x_1,x_2) \in R \times R | x_i^2 = 0} $.

    ?

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    oops. I forget how math works here...

    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeOct 6th 2009

    Use double dollar signs, or <latex> and </latex> if you want to see a preview. Also check the Instructions when you forget.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    I strenghened the proposition about microlinear loci, claiming that also in the two sheaf toposes

    \mathcal{Z} = Sh(\mathbb{L})_{finite open covers}

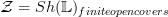
    and

    \mathcal{B} = Sh(\mathbb{L})_{finite open covers and projections}

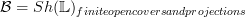
    all representables are microlinear. Either I am mixed up or this is essentially obvious. But maybe somebody feelss like checking.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    darn

    x = x x = x
    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    I don't get the dollar signs to work.

    • CommentRowNumber7.
    • CommentAuthorAndrew Stacey
    • CommentTimeOct 6th 2009

    That is just weird. A little experimenting shows that there seems to be a maximum length for subscripts. x_{finite ope} works but x_{finite open} doesn't: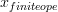 x_{finite ope} and x_{finite open}.

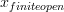    Unfortunately, as we currently ship LaTeX processing off somewhere else, there's not a lot I can about that!

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    okay, thanks Andrew, at least that tells me what's going on.

    Was a bad idea to put that novel-like text in a subscript anyway! :-)

    So here what I wanted to typeset:

    for

    \mathbb{L} = (C^\infty Ring^{fin})^{fin}

    the category of smooth loci, consider the Grothendieck topology given by

    a) covers are finite open covers

    b) covers are finite open covers and projections.

    Then sheaves wrt the first yield the smooth topos 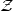\mathcal{Z} , sheaves with respect to the second the smooth topos 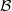\mathcal{B} , with notation as in Models for Smooth Infinitesimal Analyis (see list in appendix 2).

    I tried to add to microlinear space a (the supposedly obvious) proof that all representable objects in these toposes are microlinear.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeOct 6th 2009

    hmph

    • CommentRowNumber10.
    • CommentAuthorTobyBartels
    • CommentTimeOct 6th 2009

    Just write it out without dollar signs. We can read TeX.

    • CommentRowNumber11.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 11th 2024

    Re #1: The first definition of D(2) is correct; it is used in Moerdijk–Reyes and other sources. It gives the first-order infinitesimal neighborhood of 0.

    The definition of D(2) currently in the article is not correct; it gives a certain second-order neighborhood of 0, and it is not invariant under rotation of the x,y-plane.

    • CommentRowNumber12.
    • CommentAuthorDmitri Pavlov
    • CommentTimeJun 16th 2024

    Added:

    • F. Bergeron, Objet infinitésimal en géométrie différentielle synthétique, Exposé 10 in Rapport de Recherches du Dépt. de Math. et de Stat. 80-11 and 80-12, Université de Montréal, 1980.

    diff, v12, current

1 to 12 of 12

  1.