nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
created microlinear space
One thing I might be mixed up above:
in the literature I have seen it seems to say that
$ X^D x_X X^D \simeq X^{D(2)}$
with
$ D(2) = { (x_1,x_2) \in R \times R | x_i x_j = 0} $.
But shouldn't it be
$ D(2)' = { (x_1,x_2) \in R \times R | x_i^2 = 0} $.
?
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
oops. I forget how math works here...
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeOct 6th 2009
Use double dollar signs, or
<latex>and</latex>if you want to see a preview. Also check the Instructions when you forget. -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
I strenghened the proposition about microlinear loci, claiming that also in the two sheaf toposes
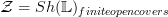
and
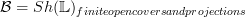
all representables are microlinear. Either I am mixed up or this is essentially obvious. But maybe somebody feelss like checking.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
darn


-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
I don't get the dollar signs to work.
-
- CommentRowNumber7.
- CommentAuthorAndrew Stacey
- CommentTimeOct 6th 2009
That is just weird. A little experimenting shows that there seems to be a maximum length for subscripts.
x_{finite ope}works butx_{finite open}doesn't: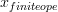 and
and 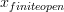 .
.Unfortunately, as we currently ship LaTeX processing off somewhere else, there's not a lot I can about that!
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
okay, thanks Andrew, at least that tells me what's going on.
Was a bad idea to put that novel-like text in a subscript anyway! :-)
So here what I wanted to typeset:
for

the category of smooth loci, consider the Grothendieck topology given by
a) covers are finite open covers
b) covers are finite open covers and projections.
Then sheaves wrt the first yield the smooth topos
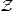 , sheaves with respect to the second the smooth topos
, sheaves with respect to the second the smooth topos 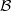 , with notation as in Models for Smooth Infinitesimal Analyis (see list in appendix 2).
, with notation as in Models for Smooth Infinitesimal Analyis (see list in appendix 2).I tried to add to microlinear space a (the supposedly obvious) proof that all representable objects in these toposes are microlinear.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeOct 6th 2009
hmph
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeOct 6th 2009
Just write it out without dollar signs. We can read TeX.
-
- CommentRowNumber11.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 11th 2024
Re #1: The first definition of D(2) is correct; it is used in Moerdijk–Reyes and other sources. It gives the first-order infinitesimal neighborhood of 0.
The definition of D(2) currently in the article is not correct; it gives a certain second-order neighborhood of 0, and it is not invariant under rotation of the x,y-plane.
-
- CommentRowNumber12.
- CommentAuthorDmitri Pavlov
- CommentTimeJun 16th 2024
1 to 12 of 12