nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
According to Peter May's Concise Topology (a page that does not yet exist, but one that I plan to write. The full name of the book is A Concise Introduction to Algebraic Topology), a numerable open cover of a space X is a locally finite open cover such that each
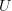in the cover is the preimage ![f_U^{-1}((0,1])](/extensions/vLaTeX/cache/latex_48ccf7de986ce5ee211e96ab2e11d9f7.png "f_U^{-1}((0,1])")
for some continuous map ![f:X\to [0,1]](/extensions/vLaTeX/cache/latex_80aae529b03b84d54763bbde2e46cc21.png "f:X\to [0,1]")
.The definition that currently resides there is the definition of a partition of unity. I might be incorrect and perhaps the defintions are equivalent, but it seems like the definition on the lab is not reconcilable with the definition in the book.
-
- CommentRowNumber2.
- CommentAuthorDavidRoberts
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
There’s a theorem of Dold, I believe, that allows one to take the ’May definition’, and refine it and form a subcover so that there is a partition of unity, and it is this refinement that is actually used (in practice). If this terminology is too much of a hijack, then we need a new name. I am of the opinion that alg. top. should be done with more sensitivity to the site (as in Top+a Grothendieck (pre)topology) used, as in algebraic geometry. “All” the results about paracompact spaces should work perfectly well, if we restrict ’covers’ in Top to mean those with a subordinate partition of unity. No one complains in Alg. geom. if a result only works for non-Noetherian schemes if the fghi topology is used. Why should it be any different if a result only works for non-paracompact spaces if it only works for the N topology (N for numerable) (or maybe we should call it the PoU topology)? tom Dieck was aware of this distinction in his paper Klassifikation numerierbarer B"undel, and I’m sure it’s in Milnor’s Construction of universal bundles II.
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
fghi topology? Anyway, the choices of topologies in AG are explained pretty well in HAG by the categorical properties they imply, rather than the finiteness properties in which they're stated.
Anyway, I feel like it would be really useful to state both definitions and cite the theorem of Dold on the page.
-
- CommentRowNumber4.
- CommentAuthorDavidRoberts
- CommentTimeMay 10th 2010
fghi topology?
;P It’s a bit like the wxyz topology, but finer.
Anyway, the choices of topologies in AG are explained pretty well in HAG by the categorical properties they imply, rather than the finiteness properties in which they’re stated.
precisely. Ditto for the N/PoU topology.
-
- CommentRowNumber5.
- CommentAuthorAndrew Stacey
- CommentTimeMay 10th 2010
@Harry: *final sentence at 3*: You should be careful making statements like that around here …
Just in case you were waiting to see if anyone else thought it was a good idea before you did it: I think that’s a good idea. Now go and do it.
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeMay 10th 2010
- (edited May 10th 2010)
I don't know the theorem of Dold, but I'll write up the ConciseRevised defn.
;P It's a bit like the wxyz topology, but finer.
I realized this after I posted, but fghi is actually pretty close to fpqc or fppf, etc. I thought it meant something like "finitely generated and homotopy invertible" or something similar.
-
- CommentRowNumber7.
- CommentAuthorTodd_Trimble
- CommentTimeMay 10th 2010
Okay, but keep the old definition in there too. I just checked with Spanier and it’s very close to what’s in there. My gut feeling is that the definitions are reconcilable.
-
- CommentRowNumber8.
- CommentAuthorHarry Gindi
- CommentTimeMay 10th 2010
Yes, I was going to put both definitions and then give a citation of the result of Dold that reconciles them, but it's pointless to put the ConciseTop version up without that theorem, since it'll just be confusing. I'll put it up as soon as someone tells me where to look up the theorem.
-
- CommentRowNumber9.
- CommentAuthorDavidRoberts
- CommentTimeMay 11th 2010
as soon as someone tells me where to look up the theorem.
and waste the practice of doing research? :)
DOLD, A., Partitions of unity in the theory of fibrations, Ann. of Math. 78, 223-255 (1963)
I believe. It’s a biggish paper for one that is scanned, so I’m afraid you’ll have to search for the result by hand. I haven’t got the paper with me at the moment, so I can’t help you as to here it is. Look for the theorem which says any ’partition of unity’ which isn’t point-finite can be replaced by one that is point-finite i.e. an actual partition of unity.
-
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeMay 11th 2010
I thought it meant something like “finitely generated and homotopy invertible” or something similar.
:P Actually that could become a serious backronym. If you do happen to invent this topology, please credit me ;-) or at least repeat my joke.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeMay 11th 2010
Does “covers admitting a subordinate partition of unity” actually form a Grothendieck topology on Top? That’s a really neat way to think about all this numerability business which hadn’t occurred to me before.
I also really enjoyed the fghi topology. I’m torn between wanting someone to invent a topology called that, so that we can tell the joke when we use it, and wanting to keep it meaningless so that we can continue to repeat the joke in appropriate contexts. (-:
-
- CommentRowNumber12.
- CommentAuthorDavidRoberts
- CommentTimeMay 11th 2010
Does “covers admitting a subordinate partition of unity” actually form a Grothendieck topology on Top? That’s a really neat way to think about all this numerability business which hadn’t occurred to me before.
yes it does. As I will keep repeating, algebraic topology should use this site and rest assured that spaces don’t have to be paracompact. If people can wait a little, I can dig out my notes tonight and I will put them up.
I’m torn between…
actually, now that you mention it, so am I.
-
- CommentRowNumber13.
- CommentAuthorDavidRoberts
- CommentTimeMay 24th 2010
- (edited May 24th 2010)
Found the ’result of Dold’, wrongly attributed to him in #9 above. The trick I was thinking of from that paper is not general enough.
Edit: btw trying to link to the comment gave me an error due to the
&focusin the url, so I’ve just linked to the thread.
1 to 13 of 13