Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Zoran: new entries

Bottom of Page

1 to 100 of 250

  1. <
  2. 1
  3. 2
  4. 3
  5. >
    • CommentRowNumber1.
    • CommentAuthorzskoda
    • CommentTimeOct 6th 2009
    • (edited Oct 6th 2009)
    New entry discrete mathematics. Appropriate change at mathematicscontents. New entry multiset, Jordan algebra.

    More will be added here as it goes, new items down.
    • CommentRowNumber2.
    • CommentAuthorTobyBartels
    • CommentTimeOct 6th 2009
    • (edited Oct 6th 2009)

    Thanks, Zoran! I have added to these, especially multiset.

    • CommentRowNumber3.
    • CommentAuthorzskoda
    • CommentTimeOct 7th 2009
    new entry crossed product algebra. One should treat the cocycle crossed products as well.
    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeOct 9th 2009
    Additions to Brown representability theorem, namely the classical version bare to bones (as stated in Switzer's monograph Algebraic topology, homotopy and homology.
    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeOct 9th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> Additions to <a href="https://ncatlab.org/nlab/show/Brown+representability+theory">Brown representability theory</a> </blockquote> <p>Thanks for that, Zoran! That was certainly missing.</p> </div>
    • CommentRowNumber6.
    • CommentAuthorzskoda
    • CommentTimeOct 15th 2009
    • (edited Oct 15th 2009)
    Added entry ringed topos, Morse function, Morse lemma. Changes to ring (1. makes sense in any symmetric monoidal category, 2. unital vs. nonunital). Changes to algebraic geometry and maybe some related items. I think one should not repeat the mistake by Dieudonne to limit the subject with one single formalism, but rather with the source of problematics, and allowing a range of formalisms. In addition SGA IV has much of what I think Urs is looking for. Not all of course.
    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeOct 15th 2009

    I added the example of ringed space and ringed site to ringed topos, and linked back and forth with lined topos.

    • CommentRowNumber8.
    • CommentAuthorMike Shulman
    • CommentTimeOct 15th 2009

    Comment on ring, and a correction to what I think you meant about symmetric monoidal categories. If that's not what you meant, then I don't know what you meant; maybe you can clarify.

    • CommentRowNumber9.
    • CommentAuthorzskoda
    • CommentTimeOct 15th 2009
    • (edited Oct 15th 2009)
    Maybe I am wrong, but I do not understand how do you define the additive abelian group in nonsymmetric monoidal category. For the multiplicative group no problem. In any case for the additive part of a notion a ring in monoidal category you need a symmetry, asking for commutativity of the ring or not. I corrected a bit back, but if I am wrong be free to correct again. However there is another sense in which I am obviously wrong: In algebra, if $A$ is a usual noncommutative ring, people often talk about $A$-rings simply as monoids in the category of $A$-bimodules. But this is a different mechanism to extend the notion of a ring -- via enrichement which is automatic in bimodules; the mechanism in symmetric monoidal category I explain is not such.
    • CommentRowNumber10.
    • CommentAuthorTobyBartels
    • CommentTimeOct 15th 2009

    I understood that we were replacing 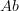Ab by an arbitrary monoidal category C, rather than replacing 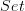Set. So C has its own notion of the additive abelian group.

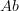    However, I think that it's very strange to refer to a monoid in an arbitrary such C as a ring in C. I would accept this if C were a monoidal additive category (with compatibility between the tensor product and biproduct), maybe even a monoidal Ab-enriched category. 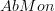Similarly, I would accept calling a monoid in C a rig in C if C were a monoidal category with compatible biproducts (making it enriched over Ab Mon but not necessarily over Ab).

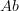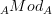    Note that this includes the case of an A-ring for A a possibly noncommutative ring; an A-ring is a monoid in {}_A Mod_A, which is a monoidal additive category.

    • CommentRowNumber11.
    • CommentAuthorzskoda
    • CommentTimeOct 15th 2009
    • (edited Oct 15th 2009)
    "However, I think that it's very strange to refer to a monoid in an arbitrary C such as a ring in C."

    I never said that. The additive par is EXPLICITLY written in terms of diagrams. Internal abelian group object makes sense in any symmetric monoidal category, like in standard alg topology books. Most often it is cartesian product, e.g. in topoi. The other part is the product. Every unital ring has two operations: one additive one multiplicative, one commutative another not. Youi hav to compatible monoid strutures. If a monoid is an algebra over an operad, or a monad, now you have two such with distributive law. The usual wisdom is that the monad for rings is composed from the monad for semigroups and monad for abelian groups with a particular distributive law. This is all very standard. Simplicial rings, dg-rings are the main examples when it is enough to say monoid as the abelia group structure is already included in the structure of the objects in the category (like A-rings). Internal rings in a topos however need additive internal belian groups defined as I stated.

    Of course I agree with Toby that one needs to be careful on rig vs ring cases.
    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeOct 15th 2009

    Just for the record, I just added a section with pointers to oo-rings ro ring, just for completeness.

    I was going to say also something leading over to ringed topos, but now Zoran has the page locked.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeOct 15th 2009

    okay, I added to ring a pointer to rings in an arbitrary topos and tried to structure the various generalizations a bit. But probably still suboptimal.

    • CommentRowNumber14.
    • CommentAuthorMike Shulman
    • CommentTimeOct 15th 2009

    Okay, so you are actually thinking of an object of a category equipped with both an "addition" morphism 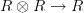R\otimes R \to R and a "multiplication" morphism 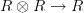R\otimes R \to R? Unfortunately you can't define a ring object that way unless your monoidal category is not just symmetric but cartesian; you need diagonal maps in order to write down the diagram saying that multiplication distributes over addition, and you also need augmentation maps in order to write down the condition that the addition have inverses.

    • CommentRowNumber15.
    • CommentAuthorTobyBartels
    • CommentTimeOct 16th 2009

    @ Zoran

    I never said that.

    I know. But it seemed that Mike was saying that.

    • CommentRowNumber16.
    • CommentAuthorMike Shulman
    • CommentTimeOct 16th 2009

    However, I think that it's very strange to refer to a monoid in an arbitrary such C as a ring in C

    I didn't mean to imply that, that was sloppy editing on my part. I agree that it only makes sense to call a monoid in C a "ring" if C is Ab-like in some way. I wouldn't require it to be literally Ab-enriched, though; it also makes sense to call a monoid object in the category of spectra a "ring spectrum."

    • CommentRowNumber17.
    • CommentAuthorzskoda
    • CommentTimeOct 17th 2009
    • (edited Oct 18th 2009)
    Mike is right, in symmetric monoidal categories beyond cartesian monoidal categories (which were the main purpose of what I wrote), one needs to have additional structures to have internal ring structure. It is not really needed to have diagonal map for the distributive law: there are exotic distributive laws which come up by different mechanisms, but these are of course less canonical.

    Now it is getting difficult to rewrite this all correctly, while still having examples both in cartesian context, and those in which the abelian group part is from underlying category, while the mulplicative semigroup is internal semigroup in the underlying category. In any case the multiplicative part is refering to the same mechanism in both cases, while the origin for the abelian group structure is different. The distributive law is again a separate issue.

    I do not understand why was the statement that internalization of groups in cartesian category is the same as requiring that the corresponding representable presheaf lifts to the presheaf of groups ? It is the standard way of thinking of internalizing groups in cartesian setup in many areas, e.g. in algebraic grometry.
    • CommentRowNumber18.
    • CommentAuthorTobyBartels
    • CommentTimeOct 18th 2009

    I think that I've rewritten it clearly and correctly; please check.

    I removed this line about A-rings:

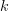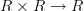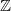    Unlike for the k-algebras, the multiplication R\times R\to R is not A-linear in the second factor, but only \mathbb{Z}-linear.

    Remember these are bimodules; the multiplication in the first factor is A-linear on the left, while the multiplication in the second factor is A-linear on the right.

    • CommentRowNumber19.
    • CommentAuthorzskoda
    • CommentTimeOct 18th 2009
    • (edited Oct 18th 2009)
    Of course the whole thing is in the category of $A$-bimodules and you are trivially right. But as left modules, what I meant it is not true, while it is true for $k$-algebras. This cropped up in the discussion by Baez et al, to which I linked the page previously. Simply said

    a(rs) = (ar)s but different from r (as), for r in A

    and not different for k-algebras. Because of lack of this axiom for k-algebras one does not say R-algebras, but R-rings for R-noncommutative.

    The statement which I said is true. Bimodules are A-Aop-modules, I am saying that is not A-linear in the second factor, hence though it is Aop/linear in the second factor, it is not A-Aop-linear in second factor either. It is A-Aop linear in the whole expression, but I am talking about SECOND factor, not about the fact that the map is in the category of A-bimodules what is trivially true. Thus I disagree with erasing, but agree with possible further explanation.

    Toby, nobody conventionally says for k-algebras algebras under k, nor for A-rings, rings under A. I was exactly pointing before to this disagreement between the general categorical wording of under-category and over-category which stems from the usage in algebraic geometry in late 1950-s and the totally accepted for much over a century wording in algebra: a $k$-algebra is said to be "algebra over $k$", the same about $A$-rings. I said "unfortunately" in earlier wording to emphasise this and somebody just erased this. I hastily restored some of the previous material including the statement about lifting representable presheaves to algebra categories as a means to transfer the definition to the cartesian caegories. The reason why it works for groups and abelian groups (and rings) is that these categories of algebras (now I am not fixing the mechanism for universal algebra here) create limits necessary to define the equations (check this, I am talking from the memory which condition on the limit is needed).
    • CommentRowNumber20.
    • CommentAuthorTobyBartels
    • CommentTimeOct 18th 2009

    Toby, nobody conventionally says for k-algebras algebras under k, nor for A-rings, rings under A.

    No, certainly not!

    Why say ‘only 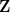\mathbf{Z}-linear’ when it is 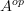A^{op}-linear? There is no asymmetry in the concept, only in a language that assumes that left is the default. A better language is to specify ‘left’ and ‘right’, as I did. In any case, ‘only’ is quite misleading.

    • CommentRowNumber21.
    • CommentAuthorzskoda
    • CommentTimeOct 19th 2009
    Surely, I did not mean any asymetry in the concept (for the right A-linearity the first factor fails), I was just originally following the phrase in the discussion on the Cafe, where C-linear was used. I am equally happy with left vs. right as with A vs Aop. You have a point that left and right is to most readers more clear.
    • CommentRowNumber22.
    • CommentAuthorzskoda
    • CommentTimeNov 4th 2009
    Added kaonization to compactly generated space as I am starting working on elementary pages for elementary intro into my course in Zagreb in Croatian (the latter is within my own pages). I got students with diverse bakcgrounds so I have to cover all fundamentals just for the case.

    The kaonization section is a discussion of Hausdorff case where the inclusion of k-spaces is having a right adjoint, as treated in Whitehead. Please check. The term kaonization for the functor I learned from Postnikov books and find it convenient although is not quite standard in western literature. On the other hand, I am interested to hear the answer to Mike/s question in another part of the entry. Toby ?
    • CommentRowNumber23.
    • CommentAuthorTobyBartels
    • CommentTimeNov 5th 2009

    You asked me to answer, but I don't know. Ronnie Brown wrote that, and my best guess as to what he meant matches Mike's guess. But I haven't thought about whether that makes the statement true.

    • CommentRowNumber24.
    • CommentAuthorzskoda
    • CommentTimeNov 14th 2009
    • (edited Nov 15th 2009)
    New entry cocylinder with redirect mapping cocylinder, corrections to the related item Hurewicz connection. New entry Gelfand-Mazur theorem with redirect Gel'fand-Mazur theorem. I wrote a query in 2-pullback: a common error in interpretation is put into the ideas at the top. Added section "noncommutative measure theory" at measure space. Changes, corrections, references and additions to H-space.
    • CommentRowNumber25.
    • CommentAuthorzskoda
    • CommentTimeNov 16th 2009
    • (edited Nov 16th 2009)
    Additions to crossed product algebra and Dold fibration. Changes to a proof in Hopf algebra. New entry (quickly written, needs formulas involving matrices, examples, noncommutative case and so on) Gauss decomposition.
    • CommentRowNumber26.
    • CommentAuthorzskoda
    • CommentTimeNov 16th 2009
    In addition to Gauss decomposition, started quantum Gauss decomposition. It is not only a decomposition of a matrix of generators as in the earlier works but as shown in my thesis, it is in fact the decomposition of certain coaction-compatibly Ore-localized subalgebras, amounting to a local trivialization of a quantum principal bundle whose fiber is quantum Borel.
    • CommentRowNumber27.
    • CommentAuthorzskoda
    • CommentTimeNov 17th 2009
    • (edited Nov 17th 2009)
    I significantly expanded crossed product algebra with material pertaining to the more general case (than the previously covered case which Hopf algebraist call smash product algebra, and which is in the top part of the entry now), namely the cocycled crossed product algebra, generalizing the factor sets (group 2-cocycles), or better to say, their linear extensions to the group algebras (at least for finite group case). This is interesting for the crows talking that the most general case of cocycles is given by homotopical algebra, I doubt that the Hopf algebraic cases could be subsumed to those in general (this is one of the easiest examples, which may be doable via homotopical algebra, but I do not know). A more invariant form of crossed product algebras is a class of Hopf-Galois extensions, namely the cleft extensions for which I just wrote an entry. And I corrected the typo in the title of the newest among Urs's private pages.
    • CommentRowNumber28.
    • CommentAuthorzskoda
    • CommentTimeNov 17th 2009
    • (edited Nov 17th 2009)
    Nobody responded about my question (posted somewhere else in this complicated system of partioned latest changes log on forum) about deformation retract. I mean should we split deformation retracts of model categories from the deformation reatracts within a single model category, like in Top. These seem to me too distinct subjects, and I do not understand the motivational connection.

    I places a query on geometric morphisms in point of a topos ? I created an entry gebras. I put it intentionally with pural as it is more dedicated to the subject than to the linguistic notion of 'a gebra', but I am open to opposite veiwpoint. I will place redirect gebra however. Added more entries to topology in associative order.
    • CommentRowNumber29.
    • CommentAuthorUrs
    • CommentTimeNov 17th 2009

    Hi Zoran,

    I don't know how these notions of deformation retracts are related, precisely, but it sure looks like they deserve separate entries.

    Concerning the query at point of a topos: I suppose that, yes, what really matters are just the isomorphism classes of topos points.

    • CommentRowNumber30.
    • CommentAuthorTodd_Trimble
    • CommentTimeNov 17th 2009
    I answered with a query of my own at point of a topos, and added a new query further down.
    • CommentRowNumber31.
    • CommentAuthorMike Shulman
    • CommentTimeNov 17th 2009

    Zoran, I think I didn't respond to your question about deformation retracts because I didn't understand what you were asking. Now that I do understand, I agree.

    • CommentRowNumber32.
    • CommentAuthorMike Shulman
    • CommentTimeNov 17th 2009
    • CommentRowNumber33.
    • CommentAuthorUrs
    • CommentTimeNov 17th 2009

    Hm, that broke all the links to this entry: most of them were intended to go to the def-retract of the homotopical version.

    I guess I'll have to go through the source entries by hand...

    • CommentRowNumber34.
    • CommentAuthorTobyBartels
    • CommentTimeNov 17th 2009
    • (edited Nov 17th 2009)

    I created an entry gebras. I put it intentionally with pural as it is more dedicated to the subject than to the linguistic notion of 'a gebra', but I am open to opposite veiwpoint.

    If a ‘gebra’ is an object, then the subject would be ‘gebra theory’ in English. Am I correct that the point is to not use the word analogously to how ‘algebra’ is used?

    • CommentRowNumber35.
    • CommentAuthorTodd_Trimble
    • CommentTimeNov 18th 2009
    I agree with Mike's reply to my second query at point of a topos, which I've now erased.
    • CommentRowNumber36.
    • CommentAuthorTobyBartels
    • CommentTimeNov 18th 2009

    After having read the article, I moved gebras to gebra theory.

    • CommentRowNumber37.
    • CommentAuthorMike Shulman
    • CommentTimeNov 18th 2009

    @Urs: sorry about breaking the links, I didn't think of that. I do think that it's the topological notion which deserves to be at the page deformation retract, though.

    • CommentRowNumber38.
    • CommentAuthorUrs
    • CommentTimeNov 18th 2009

    Right. I have fixed the links meanwhile.

    Maybe we should think about the links deformation retract for the enrichement and closed monoidal deformation retract. These of course all refer to the deformation retract of a homotopical category, so maybe their titles should be expanded.

    • CommentRowNumber39.
    • CommentAuthorzskoda
    • CommentTimeNov 18th 2009
    • (edited Nov 18th 2009)
    Toby, gebra theory is OK, thanks for keeping the redirect to gebras. I added a reference and a diagram to distributive law (and also copied the references from our entry to http://en.wikipedia.org/wiki/Distributive_law_between_monads -- as they had just two refs before).
    • CommentRowNumber40.
    • CommentAuthorzskoda
    • CommentTimeNov 18th 2009
    I added new questions to point of a topos. It is very serious question and more details will follow after I get first responses.
    • CommentRowNumber41.
    • CommentAuthorzskoda
    • CommentTimeNov 19th 2009
    On my personal area of nlab I created Beck's theorem (zoranskoda) featuring a special case.
    • CommentRowNumber42.
    • CommentAuthorzskoda
    • CommentTimeNov 19th 2009
    • (edited Nov 19th 2009)
    • CommentRowNumber43.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    • (edited Nov 21st 2009)
    Stub period meaning the period from algebraic geometry/arithmetic.

    Created birational geometry to support the citation at motive. It would be nice if somebody with inclination toward number theory would write some precise material to produce reasonable entry function field which is needed at birational geometry.
    • CommentRowNumber44.
    • CommentAuthorzskoda
    • CommentTimeNov 21st 2009
    • (edited Nov 21st 2009)

    After birational geometry, continuing in the mood of algebraic geometry, I wrote etale morphism. But then a query on Hurewitz theorem on fibrations, at Milnor slide trick.

    • CommentRowNumber45.
    • CommentAuthorzskoda
    • CommentTimeNov 25th 2009

    Additions at Legendre transform.

    • CommentRowNumber46.
    • CommentAuthorzskoda
    • CommentTimeNov 25th 2009
    • (edited Nov 25th 2009)

    Added reference Norman E. Steenrod, A convenient category of topological spaces, Michigan Math. J. 14 (1967) 133–152 to convenient category of topological spaces (and to compactly generated space), together with a link to the project euclid where it can be downloaded. The paper is not only a classical exposition of the compactly generated Hausdorff spacesm but also of the basic homotopy theory in that setup (like fibrations, NDRs etc.) with proofs. George Whitehead's book "Elements of homotopy theory" takes much from this paper but omits the proofs (in chapter I).

    • CommentRowNumber47.
    • CommentAuthorzskoda
    • CommentTimeNov 25th 2009

    I have included the proof of the main statement in Hurewicz connection: a map is a fibration iff there is a Hurewicz connection for that map.

    • CommentRowNumber48.
    • CommentAuthorzskoda
    • CommentTimeNov 25th 2009
    • (edited Nov 25th 2009)

    Urs has changed the layout, now I do not see word Theorem and word Proof in the central section. Is my browser or syntax ?

    • CommentRowNumber49.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2009
    • (edited Nov 25th 2009)

    Hm. I tried to be helpful and added the formal theorem and proof environments.

    They do display on my machine.

    I thought that using this should be preferred, since only when we use these formal environments can we eventually program the CSS style such as to format theorems etc appropriately. At the moment one advantage is that the proof environment does make an automatically generated end-of-proof box appear.

    Or at least it does on my machine! Now, I wasn't aware that this depends on the installation.

    • CommentRowNumber50.
    • CommentAuthorzskoda
    • CommentTimeNov 25th 2009

    I get the end/of/proof box well, but do not get word Theorem and do not get word Proof in that entry (neither in regular nor in print view). On IE on a new desktop which fairly well displays the rest of nlab.

    • CommentRowNumber51.
    • CommentAuthorTobyBartels
    • CommentTimeNov 25th 2009

    If you have JavaScript turned off, these environments don't appear correctly, but even then you should still get the words. Did my latest edit also remove the word ‘Definition’? Can you make a screen capture?

    • CommentRowNumber52.
    • CommentAuthorzskoda
    • CommentTimeNov 26th 2009
    • (edited Nov 26th 2009)

    Yes, the definition disappeared. I will see later what is going on, now need to hurry.

    The things work on firefox on the same computer, but the IE on that computer is quite well equipped and works for other nlab purposes and surprisingly not for this.

    • CommentRowNumber53.
    • CommentAuthorzskoda
    • CommentTimeNov 26th 2009
    • CommentRowNumber54.
    • CommentAuthorzskoda
    • CommentTimeNov 27th 2009
    • (edited Nov 27th 2009)

    I complained again at reflective subcategory. Requirement to have the localization functor left exact to use localization terminology for the unit of adjunction is not required outside of topos community. New entry simple ring.

    • CommentRowNumber55.
    • CommentAuthorTobyBartels
    • CommentTimeNov 27th 2009

    Adding details to simple ring led me to write zero ideal just for completness's sake.

    • CommentRowNumber56.
    • CommentAuthorzskoda
    • CommentTimeDec 3rd 2009
    • (edited Dec 3rd 2009)
    • CommentRowNumber57.
    • CommentAuthorzskoda
    • CommentTimeDec 15th 2009
    • (edited Dec 15th 2009)
    Added a proposition of Duško Pavlovi? on Beck-Chevalley condition into Benabou-Roubaud theorem.
    • CommentRowNumber58.
    • CommentAuthorzskoda
    • CommentTimeDec 31st 2009

    New entry Whitehead product, now not having a complete definition yet (even that may need corrections). I see that the join of spaces has been defined only at suspension. Eventually it would be good to have better and separate entry join of spaces different from suspension and join of simplicial sets. I am too tired to look into Fuks' paper who has some point in finding the Eckmann-Hilton dual of that bifunctor (for compactly generated Hausdorff spaces in his case). After Whitehead product it would be nice to have entries on Massey products and Toda brackets. These play crucial role in "secondary" constructions of Baues which are categorification of a sort which should be compared to the stuff the nlab is centered about.

    • CommentRowNumber59.
    • CommentAuthorzskoda
    • CommentTimeJan 5th 2010
    • (edited Jan 6th 2010)

    I added internal category in a monoidal category (aka noncartesian internal category) but did not spell out the main definition yet, I have to hurry to a bus right now...Bio entry George Janelidze (needs partial bibliography) and Hvedri Inassaridze.

    • CommentRowNumber60.
    • CommentAuthorzskoda
    • CommentTimeJan 6th 2010
    • CommentRowNumber61.
    • CommentAuthorHarry Gindi
    • CommentTimeJan 6th 2010
    • (edited Jan 6th 2010)
    Could you give me a reference for locally affine space in the commutative case? I'm interested in reading about it.
    • CommentRowNumber62.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010
    • (edited Jan 7th 2010)

    I suppose it should be in Gabriel-Demazure book (exists djvu) though I am not sure how much is said in that generality. It is also quoted in intro parts of some papers of Toen, Vezzosi.

    There might be something in

    • Donald Knutson, Algebraic Spaces, LNM 203, Springer 1971

    but I do not recall if the original book is treating the subject in quite that language, but to some extent it should be there.

    I have created cofibration.

    • CommentRowNumber63.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010
    • (edited Jan 7th 2010)
    • CommentRowNumber64.
    • CommentAuthorHarry Gindi
    • CommentTimeJan 7th 2010
    Zoran, in locally affine space, shouldn't those be sheaves of sets rather than rings? At least that's how schemes are constructed in the functor of points formalism, so it seems like the same construction should apply to any other subcanonical topology on CRing^op
    • CommentRowNumber65.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010

    Yes, sheaves of sets.

    • CommentRowNumber66.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010

    I have to run as well now.

    • CommentRowNumber67.
    • CommentAuthorzskoda
    • CommentTimeJan 11th 2010
    • (edited Jan 12th 2010)

    New entry arithmetic geometry and more links and references, mainly to Mikhail Kapranov and Alexander Rosenberg. Corrections to enhanced triangulated category; the three variants should not be equated in general. New details at higher monadic descent.

    • CommentRowNumber68.
    • CommentAuthorzskoda
    • CommentTimeJan 12th 2010
    • (edited Jan 12th 2010)

    Élie Cartan, , Henri Cartan, Claudio Hermida, Sophus Lie, local Lie group and some crosslinks in Timeline (I can not spell so long title without effort). Stub Verdier's abelianization functor.

    • CommentRowNumber69.
    • CommentAuthorzskoda
    • CommentTimeJan 14th 2010
    • (edited Jan 14th 2010)

    New bio entries Raoul Bott, Paul Bressler. In wikipedia Bressler is not listed among Bott's students, but I know he was.

    The entry left adjoint has antiLeibniz ordering for the composition of natural transformations; as this is used much less widely, I think as a basic item, it is more audience friendly if we rephrase it in the more standard compoisition notation and Leibniz ordering. I will not change it unless I get confirmation from others. By the way, adjoint functor is for half na hour locked by an anonymous user. Though it is implied by other definition, I think we could have a paragraph or two for adjoint pair in terms of one of the two transformations but with stating its universal property (e.g. by a counit and its universal property).

    New entries: compact operator, relatively compact subset, Fredholm operator. The purpose is of course, to set some background for the discussion of index theorems, which are closer to the central focus of the nlab. I'd like also to have entries on some relations to symplectic topology (e.g. Maslov index, Floer homology...) where the Fredholm theory is of central importance. New entries Morse theory, perfect Morse function, heat kernel. More crosslinks at geometry.

    • CommentRowNumber70.
    • CommentAuthorzskoda
    • CommentTimeJan 14th 2010
    • (edited Jan 14th 2010)

    New entries fundamental solution, Sobolev space, Lebesgue space (in the latter the title is slightly ambiguous, see the first paragraph). For the motivating context see the post above. More crosslinks at functional analysis and at analysis.

    • CommentRowNumber71.
    • CommentAuthorzskoda
    • CommentTimeJan 14th 2010
    • (edited Jan 14th 2010)

    Some additions to Chern character and another paragraph at Fredholm operator dealing with Fredholm complexes (I do not want to separate the latter unless the entry becomes huge).

    • CommentRowNumber72.
    • CommentAuthorzskoda
    • CommentTimeJan 18th 2010
    • (edited Jan 18th 2010)

    new: Janez Mr?un (well the character gets crippled in nForum, look at the redirect Janez Mrcun), foliation, integrable connection; additions to Ieke Moerdijk

    • CommentRowNumber73.
    • CommentAuthorTobyBartels
    • CommentTimeJan 18th 2010
    • CommentRowNumber74.
    • CommentAuthorzskoda
    • CommentTimeJan 18th 2010

    right, integrable distribution -- many thanks to your sharp eye

    • CommentRowNumber75.
    • CommentAuthorzskoda
    • CommentTimeJan 19th 2010
    • (edited Jan 19th 2010)

    New entry Jacobian conjecture. In CW complex, I added condition locally finite and the link to Milnor's article on geometric realization: a geometric realization of a locally finite simplicial complex is a CW complex. So the same condition for simplicial sets. Am I wrong ? (It seems so: not written in the Milnor's article; where the locally finite is useufl for other assertions; but isn't it that only locally finite simplicial complexes are Hausdorff while all CW-complexes are Hausdorff ??).

    I added few more references and crosslinks, and made small formatting changes at homological algebra and at some related items.

    • CommentRowNumber76.
    • CommentAuthorzskoda
    • CommentTimeJan 20th 2010

    I extended largely the list of related entries inalgebraic topology and created CW approximation (for now only the definition).

    • CommentRowNumber77.
    • CommentAuthorzskoda
    • CommentTimeJan 21st 2010
    • (edited Jan 21st 2010)

    In addition to the entries I anounced earlier today in other entries (wall crossing, geometric representation theory, Alexander Beilinson, BBDG decomposition theorem, Ofer Gabber) I created Victor Ginzburg and am just going to create Ivan Mirkovic. Added Alexandre Kirillov.

    • CommentRowNumber78.
    • CommentAuthorUrs
    • CommentTimeJan 21st 2010

    I wish I had a better idea of "wall crossing". If you feel like adding a brief "Idea"-section describing how you think about it, I'd very much appreciate it

    • CommentRowNumber79.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010

    Unfirtunately, I have feeling only about some special cases, and not yet the general idea. Maybe in a bit time I can get some progress...though I am at the moment more excited about trying to prove that the homotopy stable quasicategory has a Maltsiniotis strong triangulated structure, not only usual triangulated structure, as in Lurie's paper.

    • CommentRowNumber80.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    I added more references to hypersimplex hoping it will make me closer to bite the problem. New stub barycenter.

    Urs: there are 3 general areas in which I saw wall crossing: Stokes phenomenon (connecting the local WKB-solutions of (nonlinear) wave/eikonal equations across Stokes lines), representation theory (wall crossing functors) and Bridgeland stability conditions (relevant in string theory). Presumably one should understand the relation between the three.

    • CommentRowNumber81.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    I constructed a first version of overview section in wall crossing. We should have entries on isomonodromic deformation, Stokes line, Gauss-Manin connection, regular connection, Riemann-Hilbert correspondence, constructible sheaf etc. to support this more substantially. New entry Valery Lunts.

    • CommentRowNumber82.
    • CommentAuthorzskoda
    • CommentTimeJan 25th 2010

    Yesterday i was not allowed to post comments to nlab, from home address which is dynamic address, so I can understand that. But today I can not post comments to cafe (while I can to the nlab) from my official institute's address 161.53.130.104:

    Your comment submission failed for the following reasons:

    You are not allowed to post comments

    Please correct the error in the form below, then press PREVIEW to preview your comment.

    • CommentRowNumber83.
    • CommentAuthorzskoda
    • CommentTimeJan 25th 2010

    Adjective complicial has two quite distinct meanings in higher category theory.

    • CommentRowNumber84.
    • CommentAuthorMike Shulman
    • CommentTimeJan 25th 2010

    Wow, I've never heard that second meaning. Why don't they just say "dg-"?

    • CommentRowNumber85.
    • CommentAuthorUrs
    • CommentTimeJan 25th 2010
    • (edited Jan 25th 2010)

    Zoran,

    about the Cafe not letting you post:

    as I mentioned once, this is some annyoing bug or overreaction of the spam filter, that I can't do anything about. It happened to Bruce Bartlett a while ago, and he was stuck with it for some time. Unfortunately.

    I have no idea what causes this, and it shouldn't happen. In principle Jacques Distler is the only one who can do anything about this. But a quick workaround should be to use any other machine or otherwise try to get a different IP address. After a while the problem tends to go away.

    myself, I am making good experience now following Andrew's advice. When I connect now, I first log into a "VPN client" at Hamburg university. Don't ask me exactly what that is, I can only guess. But the result is that I am being proxied through the Hamburg university server and appear to any website as if I came from there. Hamburg University is not yet regarded as polluting the world with spam (though some people there are working on it ;-), so that helps me stay clear of spam traps.

    Maybe you can ask somebody at Ruder Boskovich about this. Probably they have this, too.

    • CommentRowNumber86.
    • CommentAuthorzskoda
    • CommentTimeJan 25th 2010
    • (edited Jan 25th 2010)

    No, this is the IP address of the whole internal network of our institute, so I can not change it.

    Wow, I've never heard that second meaning. Why don't they just say "dg-"?

    I guess it is reasonably good english to make an adjective complicial from complex, isn't it ? The terminology may be older than Verity's, though I don't know. But dg pertains only to a very specific kind of category, while complicial has much wider meaning pertaining to the whole case of derived geometry. So there is a complicial algebraic geometry which is for example not the same what some people call dg-schemes (dg schemes are a very old version of derived algebraic geometry which is not good in general). Plus I guess one wants to have a special term when emphasising that one does NOT mean bounded complexes from any side. I just added a quote to a new version of the entry complicial. I added the redirect complicial algebraic geometry.

    • CommentRowNumber87.
    • CommentAuthorzskoda
    • CommentTimeJan 28th 2010

    New entry Higgs bundle. References at cyclic cohomology.

    • CommentRowNumber88.
    • CommentAuthorUrs
    • CommentTimeJan 29th 2010
    • (edited Jan 29th 2010)

    thanks for finding the Higgs field, Zoran, should we call Geneva?

    I have once heard lectures on this, but I seem to have forgotten:

    so there is no condition that 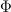\Phi satisfies a Leibnitz rule?

    And how exactly do you form 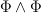\Phi \wedge \Phi ? You wedge the 1-form part and do what to the sections of E?

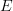    • CommentRowNumber89.
    • CommentAuthorzskoda
    • CommentTimeJan 31st 2010
    • (edited Jan 31st 2010)

    Thanks for the joke. "Higgs field" is a widespread and actually pretty standard terminology in the business of monodromy and related vector bundles, connections and differential equations; I am not much familiar with this area but I should be (some of my long-term research objectives much intersect with this); papers of e.g. Tony Pantev are the state of the art in the field.

    Thank you for your notational question: one starts with 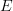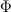E, \Phi sends it to 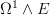\Omega^1\wedge E, then another 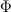\Phi acts on the 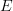E factor and the result wedge with the previously existing 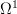\Omega^1 factor, and we get something in 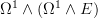\Omega^1\wedge(\Omega^1\wedge E) id est to 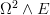\Omega^2\wedge E. Thus wedge refers to the differential forms part only while on 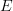E part you compose.

    • CommentRowNumber90.
    • CommentAuthorzskoda
    • CommentTimeFeb 2nd 2010
    • (edited Feb 2nd 2010)

    I have had some argument with Toby at representation. Toby is right in emphasising clean general perspective which can easily cover some of my objections. I have some doubts that not all classical notions of representation fit into this, while of course everything is OK with groups and vector spaces and their higher categorical and enriched analogues. It would be nice to say something about horizontal categorification there. I like to emphasis a concept of a symmetry which is not necessarily internal categorical notion (but surely is or should be in vast majority of cases), or whose internal origin is not yet known for some algebraic structures known to encode symmetries.

    I created from memory the book entry Gabriel-Zisman. Please check and correct, those who remember the essential content and its historical novelty and importance better. I wrote more carefully path category and added a redirect free category.

    • CommentRowNumber91.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    New entries Como, separable algebras, separable field extension (should relate it to etale morphism at some point and define separable functors!), additional remark at Catégories Tannakiennes on Magid's theory of differential Galois theory. Magid's insight into separable algebras lead Janelidze to breakthrough in the subject of categorical Galois theory, into whose entry I added additional references.

    • CommentRowNumber92.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010
    • CommentRowNumber93.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010

    Thanks for all this! Will try to look at it later. A bit short of time right now...

    • CommentRowNumber94.
    • CommentAuthorzskoda
    • CommentTimeFeb 11th 2010

    Marta Bunge, externalization (the latter vague from memory, somebody from topos theory or having more time to rethink and look into literature could write a more precise entry I hope)

    • CommentRowNumber95.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010
    • (edited Feb 12th 2010)

    Improvements at formal spectrum some stylistic, some mathematical (previous statements were true just in special cases). In particular the idea section had it wrong that the infintesimal neighborhoods are introduced with formal schemes, rather nilpotents in usual schemes can express infinitesimals: the point is that with formal schemes we can have functions depending on infinitely many neighborhoods at once. Thus not only first or second infinitesimal neighborhood but all at once. Second it is not true that the underlying space of Specf R for I-adic topology is having the same underlying space as Spec R, but the same as Spec (R/I). Once you make elements in I nilpotent the power of nilpotency does not count nilpotents do not affect the underlying space.

    • CommentRowNumber96.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010
    • (edited Feb 12th 2010)

    New entry FGA explained and related links in related entries.

    • CommentRowNumber97.
    • CommentAuthorzskoda
    • CommentTimeFeb 12th 2010

    Two new stubs: intersection cohomology, perverse sheaf.

    Noticed we do not have Poincaré duality !

    • CommentRowNumber98.
    • CommentAuthorzskoda
    • CommentTimeFeb 15th 2010
    • CommentRowNumber99.
    • CommentAuthorzskoda
    • CommentTimeFeb 16th 2010
    • (edited Feb 16th 2010)

    More at heat kernel: reference to Spin geometry and a concrete definition extracted from it (e.g. around page 208). More references at Fredholm operator.

    • CommentRowNumber100.
    • CommentAuthorzskoda
    • CommentTimeFeb 17th 2010

    I wrote five lemma in main nlab, as well as a shortened version at my personal lab, not to mess my students with the semi-abelian version section.

1 to 100 of 250

  1. <
  2. 1
  3. 2
  4. 3
  5. >