nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
Over at MO, there’s a little discussion about set theory spawned by this question, and Harry mentioned Bourbaki set theory. It occurred to me that I didn’t know the details of Bourbaki set theory (as an axiomatic theory), and I was hoping someone, perhaps Harry, could write about it since Harry periodically brings it up. I’d like to know the precise signature and axioms, and I’d like to see discussion on how it differs from other set theories (ZFC, GBC, MK, Grothendieck-Tarski, etc.). (I suspect it would be described by us as a form of “materialist” set theory.) Information on relative consistency strength and strength of expressivity would be welcome.
If no one wants to do this, I’ll try myself – but for this purpose I hope someone could provide a link to an online resource which doesn’t require a subscription. Can anyone help?
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeMay 15th 2010
I can’t answer your question for a link; the only recourse that I know is to find a university library. But I can state from memory that their foundational set theory was material, even though the use that they put it to inspired the structural approach. Also, the precise details varied with the edition; one point of interest is that they sometimes made ordered pairing a primitive operation.
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeMay 15th 2010
Also, the ‘epsilon operator’ mentioned by Harry (in a comment to your reply to which you linked above) is not the membership predicate (which Bourbaki does also have, of course), but the global choice operator. This is probably a more important deviation from ZFC’s signature than ordered pairing, and it also has a consequence in strength: one has choice for class-functions and not just for set-functions (although it is perfectly possible to put this strengthened ‘large’ axiom of choice in the terms of ZFC as well).
-
- CommentRowNumber4.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
Thanks for the info, Toby. I may break down and head off to the closest University library.
Obviously I’d like to hear from Harry, but since you seem to know something about this subject, I guess it’s okay to ask you too. What does this mean:
In Bourbaki’s formulation of set theory, there is no informal notion of a collection or class. The notion of a set is generated by means of an epsilon-operator.
I’m not at all sure what is trying to be said in the first sentence. (I mean surely there is such an informal notion whenever one conceives of a semantics for any theory whatsoever, and in that all set theories are alike.) I would guess that the second sentence could refer to an axiom scheme which allows one to construct new sets from old, but I’m not clear on what “notion of a set is generated by…” means. What does it mean to generate a notion?
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
A note before I begin:
Bourbaki's set theory is equivalent to ZGC, or Zermelo + Global Choice. It does not include the axiom of replacement, for instance, and is therefore unsuitable for modern mathematics. However, if in addition to Bourbaki set theory, you adjoin the axiom of universes from SGA4 (in the section written by Bourbaki), you have a fully functioning set theory (with universes). Let's assume then that we're working in BU=Bourbaki+Universes
Bourbaki's formalism for set construction is very strange (it is based on the work of Hilbert). Unlike standard ZFC, Bourbaki's set theory consists of: axioms, variables, and "specific signs", where the "specific signs" have syntactic rules defining their usage. The specific signs of a set theory are disjunction, negation, and a formal term called tau, which functions as a global choice operator. Everything else in mathematics is then an abbreviation of some term or relation appearing in a proof valid formal construction (defined on one of the first few pages). Bourbaki defines a set to be epsilon(Coll_X(R)) for some relation R defining a set. Coll_X is a statement that determines whether or not the relation defines a set, and epsilon realizes a distinguished set if such a set exists, where epsilon is defined via a complicated construction using tau (note that this is not the standard use of epsilon, which usually takes the place of tau). ARD Mathias wrote an article called A term of length 4,523,659,424,929, which describes how impractical it would be to write down the definition of the number "1" using Bourbaki's set theory, to illustrate what I mean. The whole point of Bourbaki's formalism is to avoid the informal notion of a class. The only thing that is taken to be informal is the formation of assemblies.
Is it useful? Probably not. Is it interesting? Maybe.
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
Well, I’m more baffled than ever (especially by your penultimate sentence, and the one preceding), but I’m intrigued. What is the distinction between the informal notion of assembly and the informal notion of class or collection?
The link to the Mathias article could be helpful; thanks. It would be even better, in fact it would be great, if you could lay out Bourbaki set theory precisely in the nLab (if that’s not too much to ask). I have a hard time guessing on the basis of your description above.
(I thought from former comments that you were much more enthusiastic about Bourbaki set theory than you appear to be in your comment! (-: I would be interested to know why you have been promoting it here and there.)
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
Oh, I would never use it, but it has a lot of ideas that I agree with about foundations. Unfortunately, the execution of these ideas isn't all that great. The fact is, I'm not interested enough in foundations to really care about what foundations I use in practice, but if I were interested in them, Bourbaki's ideas are aesthetically appealing to me.
If you want, I can e-mail you either the first edition in English, the second edition in French, or a link to either one (or both).
The part from SGA 4 that you would want to read is at the end of expose 1, where there is an appendix written by Bourbaki.
-
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeMay 16th 2010
Links to both would be wonderful; thanks. If I have trouble, I may pester you to email stuff.
It would be enormously helpful if you (or someone) could tell me how the syntax of Bourbaki set theory (or BU) is to be interpreted in standard ZGC ( ZGC + U), since Bourbaki is notoriously thin on motivations.
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
Well, disjunction and negation are standard,
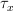 can be interpreted as Hilbert's global choice operator. The semantic links that flow out from tau to the letters replaced with boxes are exactly what they are on the page, semantic links. It is Bourbaki's formalism for elimination of free variables.
can be interpreted as Hilbert's global choice operator. The semantic links that flow out from tau to the letters replaced with boxes are exactly what they are on the page, semantic links. It is Bourbaki's formalism for elimination of free variables.The syntax is not really comparable because the tau operator makes things extremely different on a foundational level.
Redacted
If you want to find out where to download books in the future, shoot me an e-mail. The place I visit has a 95 percent success rate (the only books I couldn't find were Porter-Kamps and Hirschhorn (although I found the latter one on a russian website later on).
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
It does not include the axiom of replacement, for instance, and is therefore unsuitable for modern mathematics.
Actually, the axiom of replacement is unnecessary for huge swaths of modern mathematics. As far as I know, it mostly only crops up when you start to do transfinite induction. The classical example is Borel determinacy, which is provably unprovable in Zermelo set theory. I don’t know the foundational status of the small object argument.
-
- CommentRowNumber11.
- CommentAuthorTodd_Trimble
- CommentTimeMay 16th 2010
The syntax is not really comparable because the tau operator makes things extremely different on a foundational level.
Well, if the claim is that BU is equivalent to ZGC+U, then there had better be a means of comparison! Don’t back out on me now! :-)
Back at #7: which ideas of Bourbaki on foundations are aesthetically pleasing to you, and why? (I guess you really mean that it’s ZGC + U that is pleasing, since the presentational details of Bourbaki aren’t all that great according to you?)
Alright I’ll email them now.
Great! Many thanks.
-
- CommentRowNumber12.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
@Todd: I mean that Bourbaki's set theory starts on a much lower level than standard treatments of set theories. You start being able to compare things once you've got the definition of a set, which isn't until a bit into chapter 2. Everything becomes recognizable once the axioms are introduced (although there is a dreadful typo in the english edition of the "axiom of collection and union", which has a capital instead of a lower-case x in a subscript, which makes it so nothing makes any sense at all. Watch out for it. I wasted several hours trying to parse it (it's a fairly complicated axiom) until I looked in the "list of axioms" at the back of the book and saw that it was an error).
-
- CommentRowNumber13.
- CommentAuthorTobyBartels
- CommentTimeMay 16th 2010
@ Todd:
What is the distinction between the informal notion of assembly and the informal notion of class or collection?
As explained in Mathias, an ‘assemblage’ is a finite list of symbols from a specified finite alphabet. First-order logic, the foundation for such theories as ZFC and ETCS, is similarly based on the intuitive concept of a finite list of symbols from a specified finite alphabet, so I really don’t see why Harry is saying that Bourbaki is based on a different informal notion that ZFC or ETCS is.
Actually, both Bourbaki and first-order logic (as usually formulated) use something slightly fancier than a finite list of symbols from a specified finite alphabet. Bourbaki has (judging from Mathias, not from my own memory) the concept of linking one symbol (a binding operator) in the list with others (placeholders for bound variables). First-order logic usually starts with an infinite alphabet, giving an infinite supply of variables. Both of these tricks could be (and in some formulations of first-order logic, at least, are) avoided.
-
- CommentRowNumber14.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
@Toby: At least in ETCS and SEAR, we have informal collections of objects and arrows. If we build category theory inside of set theory, then the resolution of this is easy, since we can just call them sets (or classes if we allow something like NBG class theory). However, every other treatment I've seen of the foundations of category theory uses some informal unspecified notion of a 'collection' or a 'type', which doesn't seem very satisfying to me.
-
- CommentRowNumber15.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
Huh? ETCS and SEAR use the same first-order logic that ZFC does. Nothing informal or unspecified about it. The objects and arrows in ETCS are only unspecified in the same sense that the sets in ZFC are unspecified.
I’ve actually never seen any treatment of the foundations of category theory which used anything informal at all. The whole point of foundations is to be formal.
-
- CommentRowNumber16.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
@Harry #12: I gather from your comments about the missing axiom of replacement that this axiom of “collection and union” must have nothing to do with the axiom that usually goes by the name “collection” in ZF, since the latter is at least as strong as replacement. How are Bourbaki using the term “collection”?
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
As explained in Mathias, an ‘assemblage’ is a finite list of symbols from a specified finite alphabet.
Right – I saw that after I had posted my message (where I was merely guessing what “assemblage” might mean).
First-order logic, the foundation for such theories as ZFC and ETCS, is similarly based on the intuitive concept of a finite list of symbols from a specified finite alphabet, so I really don’t see why Harry is saying that Bourbaki is based on a different informal notion that ZFC or ETCS is.
Well, I don’t either. In fact, at this point I have no idea what Harry means when he says “we have” an “informal notion of collection” of sets in ETCS or SEAR, but not in Bourbaki set theory.
Ordinarily, if someone said this, I would interpret this collection as referring to a universe of sets out there that set theory is attempting to formalize, at least in part. On that reading, presumably Bourbaki set theory and SEAR and ZFC are all referring to the same subject matter, so how would the “informal collection” pertain to one but not the other?
On another (more formalist) reading, maybe the “informal collection” refers to the collection of objects specified by expressions within the given language – and again I don’t understand why this informal collection would adhere to one presentation of set theory (say ZGC+U) but not to another (say BU, which Harry tells us is equivalent to ZGC+U).
So, I have no idea what distinction Harry is trying to draw here.
I’ve actually never seen any treatment of the foundations of category theory which used anything informal at all. The whole point of foundations is to be formal.
Yes, precisely. What is this “informal collection”? Please tell!
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
I'm sitting here reading through "Sets for mathematics", and this notion we're talking about is given no formal definition. It's just written a,b,c...
Maybe I'm reading the wrong part of the book, but I don't see it.
The problem I'm seeing is that there's no actual formal definition given of this handwavy collection. Is there perhaps a book that covers these things with more formality?
Bourbaki gives an internal description of what a set is without resorting to having some sort of collection of abstract sets and arrows between them.
The collections that Bourbaki takes as primitive aren't the sets themselves but abstract logical variables. Saying "A is a set" means that A is a formal assembly of signs of the form
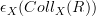 for a defining relation (predicate) R that is collectivising in X.
for a defining relation (predicate) R that is collectivising in X. -
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
Okay, I think I see. In ordinary first-order logic there is syntax and semantics. Syntactically, we manipulate symbols according to rules. Then in semantics we talk about collections of “things” which satisfy the axioms and conclude that the theorems we derived in a purely syntactic way are also valid. Of course semantics can only be made formal in the context of some external theory in which to “have” collections of things, such as a set theory of some sort. The levels get confusing when the syntactic theory in question is itself a set theory, and thus the models in question are collections of things which we call “sets,” and at first I thought that might have something to do with the confusion.
But it sounds like you’re saying that Bourbaki’s set theory isn’t actually using first-order logic at all, in that they have no variables which stand for sets? Is what they mean by a “set” what the rest of us would call a definable set, i.e. a set that can be characterized by some logical formula, so that they can “define” a set to be instead a defining formula for it? But I think even in ZGC one can prove the existence of undefinable sets, so then I’m confused about how that can be equivalent. Actually I can’t even figure out how that would make sense, since it seems that in order to define a definable set, you need to have variables ranging over the putative elements of that set.
Maybe I don’t see at all.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
Variables don't stand for anything unless we tell them to. They are the logical primitives of a theory. I can't claim to understand it in the contrast to other approaches to material set theory because the formalism is really quite strange. I can send you the book if you want to take a look at it and maybe correct some of what I've said, if I've made some elementary mistakes (note that I have not actually added anything to the lab because I'm really not comfortable with comparing it to other set theories).
A lot of the choices made in the book appear to be focused on avoiding circularity and reference to some predefined notion of a set by avoiding the creation of any sort of semantics at all.
However, I think that another source of the confusion here is that Bourbaki uses first-order logic with a hilbert-style proof calculus, rather than a "natural deduction"-style proof calculus. According to wikipedia, the most famous form of this approach is called the hilbert-ackermann proof calculus of 1928.
-
- CommentRowNumber21.
- CommentAuthorTodd_Trimble
- CommentTimeMay 16th 2010
- (edited May 17th 2010 by Mathforge Admin)
I’m sitting here reading through “Sets for mathematics”, and this notion we’re talking about is given no formal definition.
Well, yeah. Consider the intended audience.
Fully formal theories are not particularly pleasant to read or to write down, but Toby himself took up such a “challenge” a few months ago in response to a long discussion with Arnold Neumaier at the Café. I don’t know whether you saw what Toby produced. But perhaps something along these lines could be entered into the Lab, to convince skeptics that theories like ETCS are fully formalizable without reference to “informal collections”.
-
- CommentRowNumber22.
- CommentAuthorTodd_Trimble
- CommentTimeMay 16th 2010
- (edited May 17th 2010 by Mathforge Admin)
I’m sitting here reading through “Sets for mathematics”, and this notion we’re talking about is given no formal definition.
Well, yeah. Consider the intended audience.
Fully formal theories are not particularly pleasant to read or to write down, but Toby himself took up such a “challenge” a few months ago in response to a long discussion with Arnold Neumaier at the Café. I don’t know whether you saw what Toby produced. But perhaps something along these lines could be entered into the Lab, to convince skeptics that theories like ETCS are fully formalizable without reference to “informal collections”.
-
- CommentRowNumber23.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
Any chance you could give me a link? I'd be happy to abandon the system in Bourbaki. As I indicated above, it's pretty useless.
-
- CommentRowNumber24.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
Wait, I thought we were talking about Bourbaki set theory because you (Harry) liked it for some reason. If you’d be happy to abandon it too, then why are we bothering? No one else uses it or cares much about it any more, as far as I can tell. Let’s just consign it to the dustbin of history.
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
I'll be happy to abandon it if I can find a sufficiently formal exposition of a better one.
1 to 25 of 25