Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Vistoli, Notes on Grothendieck topologies, fibered categories and descent theory

Bottom of Page

1 to 32 of 32

  1.  
    • CommentRowNumber1.
    • CommentAuthorEric
    • CommentTimeMay 21st 2010

    I started adding some illustrations to my personal web related to Vistoli’s paper on descent. If you like them or have suggestions to improve them, I can maybe migrate some to nLab pages:

    Notes on Grothendieck Topologies, Fibered Categories and Descent Theory (ericforgy)

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeMay 21st 2010
    • (edited May 21st 2010)

    Hi Eric,

    I like these pictures. I think they could well be included on the relevant nLab pages.

    Just one point, which could maybe be improved: when drawing these arrows, I think it crucial to distinguish between arrows

    → \to

    that are morphisms and “mapsto” arrows

    ↦ \mapsto

    that indicate the value of a function of sets, i.e. of a morphisms of sets.

    The vertical arrow that you label h Xh_X is really a “mapsto”-arrow ↦\mapsto. Because it is really the component of a map of the morphism of sets (h X) 0:Obj(C)→Obj(Set)(h_X)_0 : Obj(C) \to Obj(Set) on a given element U∈Obj(C)U \in Obj(C).

    See what I mean?

    • CommentRowNumber3.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    Yeah. Sure. I changed the vertical arrow to mapsto.

    The next thing I was going to draw was how h f:h X→h Yh_f: h_X\to h_Y works. This is a natural transformation. But then I started wondering if this is a natural transformation, why is it so special? Why isn’t the other map with α\alpha also some kind of natural transformation?

    Since

    h X=Hom C(−,X)h_X = Hom_C(-,X)

    it makes sense (and this is probably what you do) to let

    h X=Hom C(X,−).h^X = Hom_C(X,-).

    After a picture or two, it becomes obvious that

    h f=h Y→h X.h^f = h^Y\to h^X.

    This seems perfectly natural with commuting squares and everything, but some things get switched around. Is there a such thing as contravariant natural transformation or something? What is the best way to think of h fh^f?

    • CommentRowNumber4.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

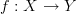    The natural transformation isn't contravariant, the co-yoneda embedding (functor) h^{(\cdot)}:C^{op}\to [C,Set] is contravariant, so it sends f:X\to Y to the natural transformation h^f:h^Y\to h^X.

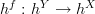    The best way to think about it is that it's postcomposition with the arrow f. If you dualize your picture by extending maps to the right by postcomposition, you will get the right picture. Since the functor is contravariant, your \mapsto arrows by the co-yoneda functor will cross in the middle. If you draw it out, it should be clear. One of the reasons why we write contravariant functors as functors from the opposite category is that you wouldn't have to have the arrows cross if you drew out the picture as a functor from the opposite category.

    • CommentRowNumber5.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    Thanks. I still get confused when I see op{}^{op} and “contravariant” in the same sentence. I didn’t realize these were the (co)-Yoneda embedding functors (I’m still leading up to Yoneda lemma).

    Just to check that I’ve got the terminology correct, it seems there are two ways (and probably more) to say exactly the same thing. For the following sanity check, I’ll denote Cov(X,Y) as the category whose objects are covariant functors and Contra(X,Y) as the category whose objects are contravariant functors. Note: I’m definitely not proposing the use of this notation for anything other than the following sanity check for my own sake.

    1. Yoneda embedding is a functor C→Cov(C op,Set)C\to Cov(C^{op},Set)
    2. co-Yoneda embedding is a functor C op→Cov(C,Set)C^{op}\to Cov(C,Set)

    or

    1. Yoneda embedding is a functor C→Contra(C,Set)C\to Contra(C,Set)
    2. co-Yoneda embedding is a contravariant functor C→Cov(C,Set)C\to Cov(C,Set)

    Is that right?

    • CommentRowNumber6.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010

    Yes.

    • CommentRowNumber7.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    Thank you :)

    • CommentRowNumber8.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Eric, I feel like you’re probably ready to actually prove the Yoneda lemma yourself. You should read the statement, draw out the diagram, and do it. I am of the opinion that this is one of the best ways to improve your intuition.

    I will help you if necessary, but the trick is to try out different test objects in the diagram until you realize what’s going on. I can provide you with the test diagram if you like, but you should perform the proof yourself.

    Hom(f,X) Hom(U,X) → Hom(U′,X) p U ↓ ↓ p U′ F(U) → F(U′) F(f) \begin{matrix} &&Hom(f,X)&&\\ &Hom(U,X)&\to& Hom(U',X)&\\ p_U&\downarrow&&\downarrow&p_{U'}\\ &F(U)&\to &F(U')&\\ &&F(f)&& \end{matrix}

    Where FF is a presheaf, pp is a natural transformation h X→Fh_X\to F, and f:U′→Uf:U'\to U. Now you must remember only one thing. F(U)F(U) is a set for any object UU. Now play around with the test objects U and U’, and you will notice that the natural transformation is determined by a single element of something. I won’t give any more away, but think about what kinds of things in categories are unique.

    If you think about functors in terms of commuting diagrams, you will not be able to prove it. Think about the axioms of a category and the standard definition of a functor. Yoneda’s lemma is a KISS (keep it simple, stupid!) proof, and adding unnecessary complications will obscure the trick.

    • CommentRowNumber9.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Baby steps…

    I’ve now added an illustration for h f:h X→h Yh_f: h_X\to h_Y.

    • CommentRowNumber10.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    … and another illustration to show it is a natural transformation.

    • CommentRowNumber11.
    • CommentAuthorMike Shulman
    • CommentTimeMay 22nd 2010

    Regarding contravariance, I feel like it is not that unreasonable to say “a contravariant functor C op→SetC^{op}\to Set” to mean the same thing as “a functor C op→SetC^{op}\to Set” – the adjective “contravariant” is just being descriptive, emphasizing the fact that the functor is defined on an opposite category. I probably wouldn’t write such a thing (if I were paying attention), but I might easily say it verbally without thinking about it. Because I really don’t believe that there is such a thing as “a contravariant functor” having a different definition from “a covariant functor” – rather there are just “functors” and we call them “covariant” or “contravariant” according to whether their source is equal to, or is the opposite of, a category we are interested in.

    • CommentRowNumber12.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    OK. So the Yoneda lemma says that for any presheaf F:C op→SetF:C^{op}\to Set, each element x∈F(X)x\in F(X) corresponds to a natural transformation x:h X→Fx: h_X\to F (abuse of notation alert).

    Given a natural transformation x:h X→Fx: h_X\to F, the corresponding element in F(X)F(X) is simply x X(1 X)x_X(1_X).

    Given an element x∈F(X)x\in F(X), the corresponding natural transformation is built component-wise via x U(f)=F *f(x)x_U(f) = F^*f(x) for each f∈h X(U)f\in h_X(U).

    This is progress, I think :)

    I still do not feel like I’ve fully grokked the significance yet though.

    • CommentRowNumber13.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Not exactly, no. It doesn’t correspond to the element you send on the identity. The whole point is to show that any such natural transformation is determined by its action on the identity map (the trick). Then, for each element of F(X), there is exactly one function mapping the identity to it. Then this gives us a natural bijective correspondence between natural transformations of h X→Fh_X\to F and elements of F(X)F(X).

    Despite the fact that I’ve written out a sketch of a proof, I suggest that you write it out fully.
    A Corollary:

    It follows by inspection of the definition of a colimit and the Yoneda lemma that every presheaf is a colimit of representable functors. This lets us “build” presheaves out of representable functors.

    With regards to the significance of the result, I’ll give an example:

    Let S be a simplicial set. Then S is a presheaf on the simplex category. However, to look at the actual n-simplices S_n, it suffices to look at maps of the n-simplex (which is the presheaf representing the nth finite nonempty ordinal) into our simplicial set S. On its own, hey, whatever, but let’s think about singular homology for a second: The set of n-simplices of the space X is given by maps of the geometric n-simplex into our space. Hmm… the geometric n-simplex is the geometric realization of the standard n-simplex. Well, we can now define an adjoint to the geometric realization functor as follows: Sing(X) n:=Hom Top(|Δ n|,X)Sing(X)_n:=Hom_{Top}(|\Delta^n|,X). It’s not hard to prove that Sing(X)Sing(X) is now a simplicial set and that SingSing defines a functor from spaces into simplicial sets. Ah, but now by the Yoneda lemma, we have that Hom SSet(Δ n,Sing(X))≅Sing(X) n=Hom Top(|Δ n|,X)Hom_{SSet}(\Delta^n,Sing(X))\cong Sing(X)_n = Hom_{Top}(|\Delta^n|,X). Goodness gracious, it’s an adjoint functor! Why is this useful? It proves that singular homology is just a special case of simplicial homology theory!

    Another one: We define the nerve of a category: N(C) n:=Hom Cat([n],C)N(C)_n:=Hom_{Cat}([n],C), where [n][n] is the nth finite nonempty ordinal considered as a category, and where CatCat is the 1-category of categories where morphisms are functors (to clarify, we’re defining the n-simplices of the nerve of C to be the functors from [n][n] to C). Then we have that Hom SSet(Δ n,N(C))≅Hom Cat([n],C)Hom_{SSet}(\Delta^n,N(C))\cong Hom_{Cat}([n],C). Hmm, a little bit strange. It makes you think that maybe there is an adjoint to this functor sending the n-simplex to the category [n], and that further, it is a left adjoint, so it commutes with colimits! Well, it exists, and has the properties we want. This is called the homotopy category functor (this is somewhat vague, since there are lots of functors with this name, but I don’t know of a better name). We can do even better, of course, but this is getting into much deeper water.

    • CommentRowNumber14.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010

    For any natural transformation τ:h X→F\tau:h_X\to F, the component τ X:h X(X)→F(X)\tau_X: h_X(X) \to F(X) sends any endomorphism f∈h XXf\in h_X X to an element τ X(f)∈F(X)\tau_X(f)\in F(X). Maybe I didn’t say it very clearly, but what I meant is that Yoneda lemma says each natural transformation τ:h X→F\tau: h_X\to F corresponds to the element τ X(1 X)∈F(X)\tau_X(1_X) \in F(X). Conversely, given any x∈F(X)x\in F(X) we can construct the corresponding natural transformation.

    • CommentRowNumber15.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Yes, that is technically correct, but I think you might be missing the point (unless you just haven’t explained what you mean clearly enough).

    The whole interesting thing is that the natural transformation is determined by the image of the identity map and naturality. The reason this is interesting comes from the proof.

    I’ll show you:

    Hom(f,X) Hom(X,X) → Hom(Y,X) p X ↓ ↓ p Y F(X) → F(Y) F(f) \begin{matrix} &&Hom(f,X)&&\\ &Hom(X,X)&\to& Hom(Y,X)&\\ p_X&\downarrow&&\downarrow&p_{Y}\\ &F(X)&\to &F(Y)&\\ &&F(f)&& \end{matrix}

    For any map f:Y→Xf:Y\to X, and everything is as above. Then clearly f=id X∘ff=id_X\circ f, so we have F(f)(p X(id X))=p Y(Hom(f,X)(id X))=p Y(id X∘f)=p Y(f)F(f)(p_X(id_X))=p_Y(Hom(f,X)(id_X))=p_Y(id_X\circ f)=p_Y(f) by commutativity of the diagram. Well, what does this say? It says that pp is determined by p X(id X)p_X(id_X). Showing that it determines it uniquely is really just a formal check.

    What you’re citing to me is the actual map we construct. This is just the formal verification of the result. The important part is what I stated. Again, I’m not sure if you actually missed the point or if you just didn’t explain it clearly, but I figure it’s worth writing out the argument in full.

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeMay 22nd 2010

    Harry,

    maybe you feell like adding some of these details into Yoneda lemma – proof. That section is presently a bit terse.

    • CommentRowNumber17.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    I’m currently improving the article operad, but since I’m rewriting a pretty big chunk of the in-depth treatment, I’ve saved it locally and will put it up when I’m finished later today.

    • CommentRowNumber18.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    In the interest of collaboration (and avoiding irritating people), why don’t you suggest ways you think the article operad could be improved in query boxes, so that we can talk about it first?

    I’m not saying there’s no room for improvement (it could certainly be formatted better), but I’d like to see what you consider an improvement before you start writing all over it. I think I wouldn’t like it at all if certain insights were overwritten.

    • CommentRowNumber19.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    No, I'm working from the original, but I'm working on clarifying the notation, formatting, fixing grammatical stuff, etc. I moved some stuff around, and I can't find a good place for the stuff about combinatorial species (so I've currently moved it down to the bottom in limbo.), but apart from that, it's just improvements and no deletions. I'm doing things like renaming the abstract tensor product that is introduced on \mathbb{P} to the "cardinal sum", which is precisely what it is. I wrote out the actual formula for the induced monoidal product along the Yoneda embedding, things like that. I think I am going to have to do a complete rewrite of one or two paragraphs, but they will incorporate everything from the original paragraphs. Basically, what I'm doing is learning from the article (and the linked nLab articles) and clarifying things that I found confusing or frustrating (from bad notation, bad grammar, bad explanation [you can tell that an explanation is bad when there is another article on the nLab with an explanation that is a lot better]).

    Anyway, if anyone has any objections to any of the changes that I'm making, we can always roll back or add query boxes.

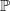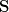    Edit: Another example: The presheaf category is denoted by Set^\mathbb{P}^op in like 30 different spots. I'm probably changing \mathbb{P} to \mathbf{S}, which is suggestive of the fact that Aut(n)=End(n)=\mathbf{S}_n for every finite cardinal n (and all other morphism sets are obviously empty, since it's a groupoid) and replacing that awful mess Set^\mathbb{P}^op either with 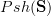Psh(\mathbf{S}) or just a nice simple \mathcal{C}.

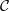    I've organized some of the insights into remarks and notes rather than keeping them in the main flow of the definition, because they are distracting. Even though this definition has some prerequisites, there's a bunch of information that really belongs separated from the actual definition. Notes and remarks are a good compromise, because they let people know what is key information and what is just interesting information without including them as footnotes. Anyway, trust me, you'll find the changes at worst innocuous.

    • CommentRowNumber20.
    • CommentAuthorEric
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Hey! I’m very happy to see Urs using some of my illustrations from my page at representable presheaf and Yoneda embedding.

    On my page I used some “soft” but, I think, description language, such as “combing strands” of morphisms forward and backward. Is any of that language appropriate for the nLab? Or do you want to keep it more formal than that? One of the things I was hoping to contribute was some more elementary/descriptive prose that might reach a different (but interested) audience.

    Edit: Nevermind :) I see Urs copied over some of my soft language as well, so I will take that as a green light, but will of course try not to be excessively soft.

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeMay 22nd 2010

    On my page I used some “soft” but, I think, description language, such as “combing strands” of morphisms forward and backward. Is any of that language appropriate for the nLab? Or do you want to keep it more formal than that?

    I think in the “Idea”-section of an entry, it is very well suited.

    Back in the beginning of the nLab we said that ideally we would want an entry to describe its topic at all possible levels of abstraction and sophistication that are useful. Introductory, expository material as well as high-powered terse definitions.

    I think every person needs a different explanation of a concept at different stages of his or her development. In a textbook one usually only has one of these levels. So some textbooks may be very good, but are still unsutied for a large class of potential readers, because they don’t pick them up where they are.

    On the wiki we are not constrained by the size limitaitons of a textbook. So we are free to put in descriptions at all levels of abstraction, to our heart’s content. If the material thus accumulated becomes too much for one page, we can simply split it off into suitable sub-pages.

    I think presently the nLab is strong much more on the formal definitions side than on the leisurely exposed material. This is because everybody puts into the Lab what is useful for him or her at a given point, and it so happens that most of the handful of contributors here happen to need material in that form for themselves.

    But John Baez for instance, of course, kept emphasizing the need for more introductory material. For instance he created pages like free cocompletion The only reason why we don’t have more of such didactic stuff is because nobody found the energy to put it in. Not because we are against having it.

    There are many aspects of the nLab (especially missing aspects) that are so not because we all want it that way, but because nobody yet found the energy to change it.

    • CommentRowNumber22.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 22nd 2010

    Basically, what I’m doing is learning from the article (and the linked nLab articles) and clarifying things that I found confusing or frustrating (from bad notation, bad grammar, bad explanation [you can tell that an explanation is bad when there is another article on the nLab with an explanation that is a lot better]).

    You sure have a way with words, Harry.

    Edit: Another example: The presheaf category is denoted by Set^\mathbb{P}^op in like 30 different spots. I’m probably changing \mathbb{P} to \mathbf{S}, which is suggestive of the fact that Aut(n)=End(n)=\mathbf{S}_n for every finite cardinal n (and all other morphism sets are obviously empty, since it’s a groupoid) and replacing that awful mess Set^\mathbb{P}^op either with Psh(\mathbf{S}) or just a nice simple \mathcal{C}.

    Not sure I like the sound of any of this. There’s not a goddamn thing wrong with ℙ\mathbb{P} (it’s completely standard), and I like exponential notation. (I think I’d be willing to part with the “op” if it were done right, since this is a groupoid we’re talking about.)

    Whatever you do, please don’t use a “nice, simple 𝒞\mathcal{C}”.

    Anyway, trust me, you’ll find the changes at worst innocuous.

    Hmm. Okay, I guess we’ll see.

    • CommentRowNumber23.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 22nd 2010

    One more thing, regarding “I’m doing things like renaming the abstract tensor product that is introduced on \mathbb{P} to the “cardinal sum”, which is precisely what it is.” That may be what it is on objects, if you identify objects with cardinals, but that is an inapt description at the level of morphisms (cardinals are ordinals which are certain ordered sets).

    If you want precision, you’d better make a note of that. For me it suffices to consider the core groupoid of the full subcategory of FinSetFinSet whose objects are [n]={1,…,n}[n] = \{1, \ldots, n\}.

    • CommentRowNumber24.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    Alright, I have unchanged the thing about 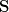\mathbf{S}, but I am keeping the Psh(blah) notation, because the exponential notation with blackboard characters is annoying to read.

    Otherwise, I've expanded the section on weighted colimits and just edited some stuff. It'll be even more innocuous now!

    Also, about cardinals, cardinals are ordinals who have forgotten their order structure, so no problemo, but I do have the thing about the core groupoid in there anyway.

    • CommentRowNumber25.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010

    Alright, I posted it in the sandbox. I don't want to just post it without you guys checking it out, since you're all skeptical. I used the underlined hom for the internal hom.

    • CommentRowNumber26.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 22nd 2010

    cardinals are ordinals who have forgotten their order structure

    Um… in ZFC, the cardinality of XX is usually defined to be the least von Neumann ordinal in bijection with XX, and a cardinal number is some such cardinality. The sentence you wrote – it’s, at best, a big question-begger. (So ω+1\omega + 1 is a cardinal if we forget its order structure? Huh?)

    I’ll check out the sandbox – thanks.

    • CommentRowNumber27.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010

    Equipotence classes of ordinals who have forgotten their order structure. We can't take equipotence classes over all sets because this leads to a paradox, but if we define a cardinal to be an equipotence class of ordinals, I think we avoid any size issues.

    • CommentRowNumber28.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 22nd 2010

    Okay, I’ve looked over the sandbox and fixed a few typos and other things. (Hit “show changes” to see what I did.) I left a little query box, but basically I think it’s fine to substitute this for the contents of the relevant section at operad. I think it could stand still more improvement, but I see what you did and why, and I appreciate the time you put into it. (I still disagree with you that the exponential notation is “annoying to read” – I and many others are totally accustomed to it – but I won’t object to its being changed in this present instance.)

    May I just register a small observation? Perhaps I’m being too sensitive, but by starting off a discussion thread by basically saying how bad something sucked:

    …I found confusing or frustrating (from bad notation, bad grammar, bad explanation [you can tell that an explanation is bad when there is another article on the nLab with an explanation that is a lot better]).

    you are bound to raise some hackles. Next time, just write under “Latest Changes” something like, “Edited operad, in an attempt to make the section on Preparation more readable. Let me know what you think.” Just be matter of fact about it, and people will appreciate your efforts much more. Thanks!

    • CommentRowNumber29.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 22nd 2010
    • (edited May 22nd 2010)

    It's another case of me seeming like a huge jerk because you can't hear the way I meant that statement. I apologize if I've hurt anyone's feelings, it was not intentional. To clarify, that was a list of all things that could possibly be wrong with an article, not my findings on this one in particular.

    • CommentRowNumber30.
    • CommentAuthorHarry Gindi
    • CommentTimeMay 23rd 2010

    Alright, I made some further changes at the sandbox (I fixed some artifacts of old notation I was using when I was originally writing up the section, which made it rather difficult to follow (right around the section about currying)). I've indented the notes, remarks, the warning, and the example, and tried to change the "restriction to the second coordinate" to something about currying, but I had a rather difficult go of figuring out how to use it in a sentence, so I gave it a shot, but I can't say whether or not the sentence is any better. I fixed some missing articles before words, and I think that it should be pretty good now.

    • CommentRowNumber31.
    • CommentAuthorTodd_Trimble
    • CommentTimeMay 23rd 2010

    Harry, this looks better and better. I’ll port it over.

    Regarding #29: I don’t think I’m actually to blame :-), but let’s move on.

    • CommentRowNumber32.
    • CommentAuthorUrs
    • CommentTimeMay 24th 2010

    Good to see the productive result at operad come out of this!!

1 to 32 of 32

  1.