nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeOct 8th 2009
pairing — pretty simple, but not to be confused with the product
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeOct 9th 2009
copairing, with examples at interval object.
domain, as disambiguation
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeOct 9th 2009
<div> <blockquote> <a href="https://ncatlab.org/nlab/show/copairing">copairing</a> </blockquote> <p>Thanks. Reminds me that I don't have the font installed that you use for the coproduct...</p> </div> -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeOct 9th 2009
<div> <blockquote> <a href="https://ncatlab.org/nlab/show/pairing">pairing</a> — pretty simple, but not to be confused with the product </blockquote> <p>Was that a hind in my direction, yb the way? I think I may have written "product" for "pairing" here and there. Not that I can't tell one from the other, but maybe I was not using good terminology.</p> </div> -
- CommentRowNumber5.
- CommentAuthorTobyBartels
- CommentTimeOct 9th 2009
It wasn't meant to be a hint, but I wrote it to link it from interval object, where you had not only written ‘product’ for ‘pairing’ but had also denoted copairing as if it were a coproduct.
But I fixed all that.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeOct 9th 2009
Do you mean writing
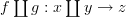 ? Isn't that standard notation?
? Isn't that standard notation? -
- CommentRowNumber7.
- CommentAuthorTobyBartels
- CommentTimeOct 10th 2009
It's not the standard that I'm aware of.
If
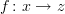 and
and 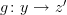 , then
, then 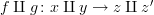 .
.But if
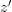 is the same as
is the same as  , then we also have
, then we also have ![[f,g]\colon x \amalg y \to z [f,g]\colon x \amalg y \to z](/extensions/vLaTeX/cache/latex_806e07c86f22057bd07091be20aa47da.png) .
.The relation between these (or rather, their duals) is discussed in detail at pairing.
There are lots of notations for the copairing
![[f,g] [f,g]](/extensions/vLaTeX/cache/latex_0b6f91eb9fe8e7fcd3fbf9cce47363a9.png) and I suppose that somebody might write it as
and I suppose that somebody might write it as 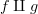 , but that conflicts with the idea that
, but that conflicts with the idea that 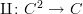 is a functor, which is reflected in my
is a functor, which is reflected in my 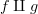 . Of course, if you keep track of the targets, then there's no actual conflict, but it doesn't seem right to me.
. Of course, if you keep track of the targets, then there's no actual conflict, but it doesn't seem right to me. -
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeOct 10th 2009
- (edited Oct 10th 2009)
I'm not sure that there is a strong consensus on notation here; my own has been to use
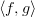 for pairing and
for pairing and 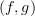 for copairing. Like Toby, I would reserve
for copairing. Like Toby, I would reserve  (or more often just
(or more often just 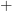 ) for the bifunctor.
) for the bifunctor.Wait: how do I activate LaTeX formulas here again? [Note: I've edited after figuring this out]
-
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeOct 10th 2009
Okay, testing...
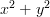
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeOct 10th 2009
Okay.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeOct 10th 2009
I agree that there's no consensus on notation, but I also agree that
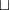 or
or 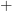 should be reserved for the bifunctor.
should be reserved for the bifunctor.
1 to 11 of 11