nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorJohn Baez
- CommentTimeJul 16th 2010
I added some more information under Frobenius algebra. I would like to add the axioms in picture form, but I haven't figure out how to upload pictures yet. I'm sure I could figure it out if I wanted... -
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeJul 20th 2010
Perhaps reading these instructions will help motivate you to figure it out. (I’m assuming that you already have a picture and you only need to figure out how to upload it.)
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeJul 20th 2010
By the way, I also put the bibliograph all in one place and inserted internal links to it. I hope that works for you.
-
- CommentRowNumber4.
- CommentAuthorJohn Baez
- CommentTimeJul 20th 2010
- (edited Jul 20th 2010)
Yes, the bibliography is great, Toby! Thanks!
I just added a few more references, and, more importantly, added lots of pictures to Frobenius algebra. Thanks for pointing me to the directions. It was really easy.
This page is getting reasonably nice. I can think of tons more to add, but I should move on!
-
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeJul 20th 2010
Nice. That is one thing the nLab has really been deficient in so far… pictures.
-
- CommentRowNumber6.
- CommentAuthorJohn Baez
- CommentTimeJul 20th 2010
I’ve got a fair number of pictures in This Week’s Finds, though not nearly enough really pretty ones… I grabbed most of those related to Frobenius algebras and put them here. I hereby authorize anyone to do the same: grab pictures from This Week’s Finds and stick them here!
-
- CommentRowNumber7.
- CommentAuthorKevin Lin
- CommentTimeJul 20th 2010
- (edited Jul 20th 2010)
Some of the contents of this MO post might be good to transfer over to the nLab page for Frobenius algebra? -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJul 20th 2010
Kevin, if you have the energy, you are invited to add content to the nLab page.
-
- CommentRowNumber9.
- CommentAuthorKevin Lin
- CommentTimeJul 20th 2010
Yes, this was my attempt to get someone else to do it ;)
But yeah, I'll try to get around to it... -
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeJul 20th 2010
Posting comments that you know of something to nForum will not produce collaborators, but requests :) Colaborators are usually produced in nlab by starting or updating an entry and posting the news of progress, then people peek in and improve.
-
- CommentRowNumber11.
- CommentAuthorTobyBartels
- CommentTimeJul 20th 2010
@ Kevin
All you really have to do is to add this to an appropriate spot on the nLab page (or create a spot for it, perhaps near the bottom):
Some of the contents of this MO post might be good to transfer here.
-
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeAug 13th 2011
I have added a Properties section to Frobenius algebra, in part to create links to the notions of quasi-Frobenius algebra and pseudo-Frobenius algebra. There is plenty of scope for expansion, since one can prove lots of nice properties hold for Frobenius algebras.
-
- CommentRowNumber13.
- CommentAuthorjim_stasheff
- CommentTimeAug 14th 2011
We need a better mnemonic - how can anyone remember which is quasi and which is pseudo and which is weak and... -
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeAug 14th 2011
Good question. But I have no idea what to do about it, since it’s the established terminology. Just suck it up, I guess. :-)
-
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeAug 15th 2011
Has anyone any ideas how Turaev’s Frobenius crossed G-algebras and Ralph Kaufmann’s variant of this fits into the overall picture?
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeJun 10th 2013
- (edited Jun 10th 2013)
Somebody writes by email the following about Frobenius algebra. I have no time to look into it right now, maybe somebody who was involved in writing the corresponding part finds a minute:
when discussing the PRO(P)s for various kinds of Frobenius algebras, you have possibly exchanged the roles of Span(FinSet) and Cospan(FinSet) (both symmetric monoidal categories with respect to the coproduct). Indeed, if I understand correctly the reference [Rosenburgh etal. 2005], they prove that Cospan(FinSet) is the PROP for for special commutative Frobenius algebras. (Also, it is not hard to prove direclty that, as a symmetric monoidal category, Cospan(FinSet) is equivalent to the category obtained by quotienting 2Cob by the relation m \circ \delta = id ; but it does not work with Span(FinSet)…)
On the other hand, I can’t quite understand the example of the PROP for bimonoids. (Well, I’m pretty sure now it can’t be Cospan(FinSet)!) Indeed, I would need some more time to understand the reference [Lack 2008], or the reference therein to [Pirashvili, “A PROP to bialgebras”], which seems relevant. But can you confirm to me that (Span(FinSet), \coprod) is the PROP for bialgebras?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeNov 18th 2014
Back then some kind soul provided these cobordism pictures at Frobenius algebra. Is that somebody still around and might easily provide also the picture for the Cardy condition?
-
- CommentRowNumber18.
- CommentAuthorRodMcGuire
- CommentTimeNov 18th 2014
Back then some kind soul provided these cobordism pictures at Frobenius algebra. Is that somebody still around and might easily provide also the picture for the Cardy condition?
I assume you mean such things pictures as commutative_law.jpg (IS THERE ANY WAY TO EMBED IMAGES IN THE NFORUM?)
Those pics come from
How is what you want different?
-
- CommentRowNumber19.
- CommentAuthorTim_Porter
- CommentTimeNov 18th 2014
- (edited Nov 18th 2014)
The Cardy condition seems to be in here
Look at 1.14.
So, Urs, see if Aaron has the xypic code still around.
-
- CommentRowNumber20.
- CommentAuthorRodMcGuire
- CommentTimeNov 19th 2014
So, Urs, see if Aaron has the xypic code still around.
The xypic code is in the TeX source in the ArXiv.
However John probably just “screen captured” (print screen) from a display of the PDF and used something like MS-Paint to crop down the bitmap and save it as a JPEG. I’d do it for you but I don’t have convenient place to host the image for upload into the nLab.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeNov 19th 2014
Please do! Upload the image to the nLab itself, as described here. Thanks.
-
- CommentRowNumber22.
- CommentAuthorRodMcGuire
- CommentTimeNov 20th 2014
- (edited Nov 20th 2014)
Ok, I followed the bizarre process for uploading an image (in the Sandbox).
cardy_condition.jpg, screen captured from Lauda & Pfeiffer 2006
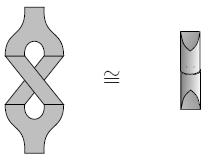
I did this on my machine with Adobe Acrobat at 150% magnification which might give different sized bitmaps on machines with different screens. If you think this image should be a different size, or want more of the related images, Capturing a screen dump is trivial, but you also need something simple like MS-Paint to crop and save the image.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeNov 20th 2014
Thanks! I have included that at Cardy condition.
-
- CommentRowNumber24.
- CommentAuthorMike Shulman
- CommentTimeAug 1st 2016
We have a stubby page Frobenius monoid that seems to be intended to be about an abstract categorical version of a Frobenius algebra. However, much of the page Frobenius algebra is already written in the generality of an arbitrary monoidal category. So I think we should either get rid of Frobenius monoid and redirect it to Frobenius algebra (and add a bit of discussion), or else try to separate the abstract from the concrete versions. My inclination is the former; any other opinions?
-
- CommentRowNumber25.
- CommentAuthorDavidRoberts
- CommentTimeAug 1st 2016
I think the first version is probably best.
-
- CommentRowNumber26.
- CommentAuthorTodd_Trimble
- CommentTimeAug 1st 2016
It looks like this has already been done, but sounds good to me.
-
- CommentRowNumber27.
- CommentAuthorMike Shulman
- CommentTimeAug 1st 2016
Yes, I went ahead and did it, but then got called away before I could announce it. I also incorporated a couple of “TODO”s from the bottom of the page into Frobenius algebra, and started adding a bit about Frobenius monoids in polycategories.
-
- CommentRowNumber28.
- CommentAuthorMike Shulman
- CommentTimeAug 1st 2016
I added a bit more, including a claim that the free polycategory containing a Frobenius algebra is the terminal polycategory.
-
- CommentRowNumber29.
- CommentAuthorTodd_Trimble
- CommentTimeAug 1st 2016
Oh, hey, that’s pretty neat!
-
- CommentRowNumber30.
- CommentAuthorMike Shulman
- CommentTimeAug 1st 2016
Isn’t it? I’m not sure quite what to make of it.
-
- CommentRowNumber31.
- CommentAuthorMike Shulman
- CommentTimeApr 24th 2019
Any Frobenius algebra A has an invariant induced by composing the unit of the multiplication with the counit of the comultiplication, Iη→Aε→I. What is this called? Is it ever interesting?
-
- CommentRowNumber32.
- CommentAuthorDavid_Corfield
- CommentTimeApr 24th 2019
Some such composition occurs, but unnamed, e.g. Fig. 11 of this.
-
- CommentRowNumber33.
- CommentAuthorMike Shulman
- CommentTimeApr 24th 2019
Thanks! At least they give it a notation, β1(A).
I notice that their definition of “special Frobenius algebra” is different than the one at Frobenius algebra: we require μ∘δ=1, whereas they require that μ∘δ and ε∘η are a nonzero multiple (in their ℂ-linear context) of the identity. I guess the relationship is that in the latter case, one can multiply ε by the invertible scalar μ∘δ and divide δ by the same scalar to get another Frobenius structure on the same underlying algebra in which μ∘δ=1 as in our definition, but that still leaves the condition that ε∘η is invertible – is that somehow implied by our definition?
-
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeOct 7th 2019
-
- CommentRowNumber35.
- CommentAuthornLab edit announcer
- CommentTimeDec 5th 2022
Clarified the definition of Frobenius algebras in the category of Vectᴋ by making the non-degenerate pairing more explicit. The previous expression was the map u ↦ ϵ∘μ(1 ⊗ u); however, interpreting the symbols on the right-hand side completely literally in their syntactic form, then by the axioms of a unital associative we have that ϵ(μ(1 ⊗ u)) = ϵ(u) ∈ K. We are trying to have the right-hand side land in V*, which is done by clarifying that the right-hand side should actually be v ↦ ϵ∘μ(v ⊗ u), which is indeed an element of V* and the desired isomorphism of V with V*.
Lillian Ryan Uhl
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeAug 11th 2023
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeAug 14th 2023
-
- CommentRowNumber38.
- CommentAuthorperezl.alonso
- CommentTimeAug 14th 2023
- (edited Aug 14th 2023)
(followup to #33) What reference are we using in Frobenius algebra for special FA’s? In Definition 2.22.iii of FFRS06 they define a special FA as a FA s.t. μΔ=βAidA and ηε=β1id1. In p.5 of Yadav22 they use the same definition for special FA but also state that a FA only satisfying the first condition is a separable Frobenius algebra.
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeAug 15th 2023
- (edited Aug 15th 2023)
I have added text (here) to show the slightly different conventions for “special Frobenius” used in the literature.
For what it’s worth, a Google search for
Frobenius algebra "called special"gives me the top hit, the second & the third all agreeing that the condition is “prod∘coprod=id”, while the FRS definition shows up only in later hits.
In any case, the entry should list all conventions instead of silently picking one — which it does now, but please be invited to add further references etc.
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeAug 21st 2023
-
- CommentRowNumber41.
- CommentAuthornLab edit announcer
- CommentTimeJul 18th 2024
-
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeJul 28th 2024
-
- CommentRowNumber43.
- CommentAuthornLab edit announcer
- CommentTimeAug 26th 2024
Added doi information for the paper
- {#Street2004} Ross Street (2004), Frobenius monads and pseudomonoids, J. Math. Phys. 45. (doi:10.1063/1.1788852)
Anonymouse
-
- CommentRowNumber44.
- CommentAuthornLab edit announcer
- CommentTimeAug 26th 2024
Also removed query box
+–{: .query} Mike Shulman: I have not carefully checked the above statement, but it seems that the Frobenius laws should suffice to manipulate any such composite into any other. Personal communications from other people who should know are in agreement. =–
Anonymouse
1 to 44 of 44