Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: simplicial deRham complex

Bottom of Page

1 to 5 of 5

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeOct 20th 2009

    I started an entry simplicial deRham complex

    on differential forms on simplicial manifolds.

    In parts this is for me to collect some standard references and definitions (still very incomplete on that aspect, help is appreciated -- is there a good reference by Dupont that is online available?)

    and in parts this is to discuss the deeper abstract-nonsense origin of this concept.

    I am thinking that

    • with differential forms understood in the synthetic context as just the image under Dold-Kan of the cosimplicial algebra of functions on the simplicial object of infinitesimal simplices in some space

    • it follows that the simplicial deRham complex of a simplicial object is just the image under Dold-Kan of the cosimplicial algebra of functions on the realization of the bisimplicial object of infinitesimal simplices in the given simplicial space.

    This looks like it is prretty obvious, once one stares at the coend-formula, but precisely that makes me feel a bit nervous. Maybe i am being too sloppy here. Would appreciate you eyeballing this.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeOct 20th 2009

    Here is probably what I need to know:

    let 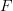F be a bisimplicial abelian group and 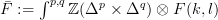\bar F := \int^{p,q} \mathbb{Z}(\Delta^p \times \Delta^q) \otimes F(k,l) the simplicial abelian group obtained as the 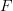F-weighted colimit over the simplicial abelian group \mathbb{Z}(\Delta^p \times \Delta^q) .

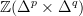    Then is under Dold-Kan the image of $\bar F$ quasi-isomorphic to the total complex of F?

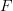    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeOct 20th 2009

    Oh, this IS just the Eilenberg-Zilber theorem, right?

    I just need something like exercise 1.6 in chapter 4 of Goerss-Jardine which should give me that 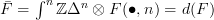\bar F = \int^n \mathbb{Z}\Delta^n \otimes F(\bullet,n) = d(F) and then Eilenberg-Zilber says d(F) \simeq Tot F .

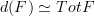    Am I on the right track here? Am a bit in a haste, unfortunately...

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeOct 20th 2009

    Sorry for all the self-replies.

    I have now typed the "supposed proposition" and its "supposed proof" into the page

    simplicial deRham complex --> reformulation in SDG.

    (scroll down a wee bit).

    Sanity checks are still very welcome.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeOct 20th 2009

    I am now pretty confident of the proof at

    simplicial deRham complex -> reformulation in SDG.

    I have also added on my personal web the page infinitesimal path oo-groupoid --> relation to simplicial deRham complex accordingly

1 to 5 of 5

  1.