nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeOct 28th 2009
created stub for simplicial manifold
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeOct 29th 2009
added the statement that simplicial manifolds are cofibrant in
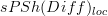 and that every cofibrant object there is weakly equivalent to a simplicial manifold.
and that every cofibrant object there is weakly equivalent to a simplicial manifold.(In view of the tower of classical literature on simplicial manifolds, this is a useful statement to keep in mind...)
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
corrected the very last sentence at simplicial manifold in the light of my recent discussion with Mike at model structure on simplicial presheaves on cofibrant objecs in the local projective model structure.
It's still a noteworthy statement, though: every oo-stack on Diff may be presented by a simplicial manifold.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeNov 17th 2009
The last statement, while well-known in various formalisms, has a nontrivial proof in some of the interpretations of the statement. For example, it assumes a standard strictification result. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 17th 2009
- (edited Nov 17th 2009)
What do you have in mind?
I was thinking of Dugger's cofibrant replacement functor, which works generally. Its existence shows that every simplicial presheaf in the projective model structure is weakly equivalent to one that is degreewise a coproduct of representables.
There is some discussion behind the scenes, by the way, that statements like this ensure that models like Chris Schommer-Pries' recent finite dim model of the string 2-group have to exist. But of course one should be aware that the general statement by Dugger only ensures that models consisting of possibly uncoutable disjoint unions of manifolds of finite but arbitrary high dimension exist.
-
- CommentRowNumber6.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 24th 2020
1 to 6 of 6