Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: loopy

Bottom of Page

1 to 6 of 6

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeOct 29th 2009

    I added an "idea" to loop space . Not claiming, though, that everybody will find this idea the most helpful one. But to some extent I think it is.

    I had another look at delooping

    Eric, you drew some nice-looking diagrams there in the discussion section. At some point in the discussion I say that I don't understand these diagram. I still don't! :-)

    It would be nice if we could converge on this, because then we could move the diagrams out of the discussion into the text as a useful illustration.

    Could you describe in words what you mean these diagrams are depicting? I am guessing that probably we are just thinking of what an arrow and a point means in such a diagram differently. Let's sort this out. If we agree that the diagrams make sense they should feature more prominently, if we come to the conclusion that there is some misunderstanding we should put a clearer warning to the reader.

    • CommentRowNumber2.
    • CommentAuthorEric
    • CommentTimeOct 29th 2009

    That sounds great. The worst case is I'LL learn something :)

    It will take me a moment to remember what was going on. Chances are I was just completely confused (as usual).

    • CommentRowNumber3.
    • CommentAuthorEric
    • CommentTimeOct 29th 2009
    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeOct 29th 2009
    • (edited Oct 29th 2009)

    Ah, thanks. See, that was helpful. Now I finally understand what you had in mind! Previously I had no clue what you meant to depict!

    Okay, right so I think I perfectly agree with the revised discussion you have at erifcorgy:Delooping: if you insist on drawing a single copy only of the contant functor G --> BG then it should look like a straight line with a 2-arrow going from it to itself.

    i see why you may like this. But I think for most computations and most reasoning about this stuff it is much more useful to draw two copies.

    See for instance the composite squares at fibration sequence or at string structure. (these are all filed invisibly with a 2-morphism as we are talking about). Each single of these squares is not a delooping square. But some of them compose to rectangles that are. This gives a nice rectable-pasting calculus that is quite powerful, as far as the utility of the statements derived from it go. I would be inclined to think that in the flattened notation you would prefer this kind of graphical computation becomes hard to do.

    You know, I said this before: just as hard as taking an equation in a single variable x and trying to write all copies of x on top of each other try this with some polynomial

    f(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^4 + a_4 x^5 .

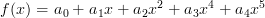    What you are suggesting for these diagrams is exactly analogous to the suggestion that this expression shouldn't be typeset this way but somehow with all the x s on top of each other.

    • CommentRowNumber5.
    • CommentAuthorEric
    • CommentTimeOct 29th 2009
    • (edited Oct 29th 2009)

    Cool. See? I DID learn something :) Thanks

    I can appreciate why you like to do things the way you do. Especially when considering limitations of itex and 2-d diagrams. I just find it a little confusing, but I think I can deal with it.

    Edit: Sorry, I removed some embarrassing comment :)

    • CommentRowNumber6.
    • CommentAuthorGuest
    • CommentTimeOct 30th 2009
    Added small section to loop space about local homotopy properties of loop spaces, as well as a (conjectural) theorem, rigorous in low dimensions, about the status of the Trimble fundamental n-groupoid as an internal n-groupoid.

    -David Roberts

1 to 6 of 6

  1.