Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: lambda ring structure of cycle ring

Bottom of Page

1 to 11 of 11

  1.  
    • CommentRowNumber1.
    • CommentAuthorGavinWraith
    • CommentTimeOct 29th 2009

    I need some help with a little computation. Let us denote by C_n an n-cycle, thought of as a finite set equipped with a permutation. All such objects are sums of cycles. For any set S let L_j(S) denote the set of j-element subsets of S. This functor on finite sets lifts to a functor on finite sets equipped with a permutation. I would like to know what is the cycle-decomposition of L_j(C_n). It is sufficient to know this when n is a power of a prime p. Evidently L_j(C_n) can be expressed as a sum of cycles of size dividing n. Can anybody come up with a nice generating function or iterative scheme for the coefficient of C_m in L_j(C_n)? It must be well known.

    • CommentRowNumber2.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 29th 2009

    Gavin, have you tried your question over at Math Overflow? I'll bet someone there could answer the question, although some of the the combinatorialists might not grab onto it immediately if the word "functor" is in there. :-)

    • CommentRowNumber3.
    • CommentAuthorTodd_Trimble
    • CommentTimeOct 30th 2009
    • (edited Oct 31st 2009)

    I think I have an outline of an iterative scheme.

    Let's focus throughout on the case n = p^r and think of our n-element cycle as Z/n, acting on itself by translation. Translation by k mod n stabilizes a subset only if the subset is a union of translates of the subgroup generated by k. For example, if j is prime to n, then the stabilizer of any j-element subset is trivial, and then L_j(C_n) will be a sum of a bunch of n-cycles, 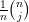\frac1{n}\binom{n}{j} in all.

    If a j-element subset has non-trivial stabilizer, say of order p^k with 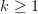k \geq 1, then that subset will be a union of translates of the order p subgroup generated by p^{r-1} mod p^r. The translating elements may be identified with elements in Z/p^{r-1}, and there will be j/p of them. A little thought shows that the cycle structure on the collection of j-element subsets with nontrivial stabilizer will be the same as that of L_{j/p}(C_{n/p}).

    This gives our iterative scheme:

    L_j(C_n) = sum of a bunch of n-cycles, if gcd(j, n) = 1.

    L_j(C_n) = L_{j/p}(C_{n/p}) + sum of a bunch of n-cycles, if p divides gcd(j, n).

    For example, L_4(C_8) has 70 elements, and breaks up as L_2(C_4) + eight 8-cycles, or as L_1(C_2) + one 4-cycle + eight 8-cycles = one 2-cycle + one 4-cycle + eight 8-cycles.

    For another, L_6(C_16) has 8008 elements, and breaks up as L_3(C_8) + i 16-cycles, where L_3(C_8) has 56 elements and i = (8008 - 56)/16. So L_6(C_16) = seven 8-cycles + 497 16-cycles.

    • CommentRowNumber4.
    • CommentAuthorGavinWraith
    • CommentTimeOct 30th 2009

    Thanks Todd. I had looked at the L_4(C_8) for inspiration too. My trouble with combinatorial questions is that I can never be quite sure that I have thought of all the possibilities, or that I have not counted something twice. The cycles form a rig, with the C_n (n > 0) an additive basis, with multiplication C_mC_n = aC_b where a = hcf(m,n) and b = lcm(m,n). But of course this rig also has a lambda-rig structure, given by the L_j operations. If one identifies this rig with the trace of the category of finite sets and functions the lambda-structure is not induced by endofunctors. However since the trace is also that of the subcategory of finite sets and bijections, the lambda-structure is induced by endofunctors on that subcategory. My instincts tell me that this lambda-rig structure is as much as we can hope for; that the L_j functors and sum and product generate all the endofunctors of the category of finite sets and bijections. I suspect that this may be well known in some other guise.

    • CommentRowNumber5.
    • CommentAuthorGavinWraith
    • CommentTimeOct 31st 2009

    I had forgot the cycle-rig's exponential structure.

    • CommentRowNumber6.
    • CommentAuthorTodd_Trimble
    • CommentTimeNov 1st 2009
    • (edited Nov 3rd 2009)

    This discussion reminds me of the Cafe and Lab discussion on Schur functors, where we are considering the generation of endofunctors on the category of finite-dimensional vector spaces.

    Since there may be other people looking on, I'm going to add some words I used to explain some of this to myself. The rig in question can be identified with the Burnside rig of the group of integers Z. That is to say, the rig of isomorphism types of finite sets X equipped with a permutation, or equivalently of sets X equipped with a Z-action, with addition given by taking coproducts or disjoint sums and multiplication given by taking cartesian products.

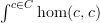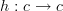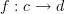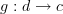    Coming back to the lambda rig structure in a moment, the trace of a category C is defined to be the coend \int^{c \in C} \hom(c, c). In more concrete terms, it consists of the collection of all endomorphisms h: c \to c, modulo the smallest equivalence relation ~ for which fg ~ gf whenever we have f: c \to d and g: d \to c. Let [h] denote the equivalence class. When C = Fin is the category of finite sets and functions, we see that any [h] can be identified with a class [h'] where 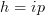h = i p is the epi-mono factorization of h and 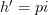h' = p i. By iterating 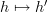h \mapsto h' enough times, one eventually stabilizes to a bijection (namely, the restriction of 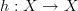h: X \to X to the stable subset 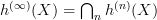h^{(\infty)}(X) = \bigcap_n h^{(n)}(X), on which h is an surjective endofunction and hence a bijection). Hence the trace of Fin is the same as the trace of FB, the category of finite sets and bijections, and this is the set of conjugacy classes of permutations as recorded by cycle-type decompositions.

    Moreover, given a category C with coproducts and products, there are maps

    \hom(x, x) \times \hom(y, y) \to \hom(x+y, x+y) \qquad \hom(x, x) \times \hom(y, y) \to \hom(x \times y, x \times y)

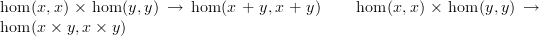
    and these descend to addition and multiplication operations

    +: Tr(C) \times Tr(C) \to Tr(C) \qquad \cdot: Tr(C) \times Tr(C) \to Tr(C)

    which give Tr(C) a rig structure provided that products distribute over coproducts in C. In the case C = Fin, these are nothing but the rig operations on the Burnside rig of Z.

    I'm finding the discussion tricky because there is ever-present danger of my making a slip between levels, but the lambda operations 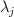\lambda_j at the rig level Tr(Fin) = Tr(FB) come about by applying trace to the endofunctor

    \Lambda_j[-]: FB \to FB

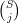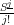    which maps a set S to the set of j-element subsets of S, which could also be written \binom{S}{j} or \frac{S^{\underline{j}}}{j!}. This last expression is a little tricky: it's supposed to indicate a categorified "falling power"; as a Joyal species, I believe it's the species \Lambda_j[-] attached to the analytic functor expression

    \Lambda_j(X) = X^{\otimes j}/j! \otimes \exp(X)

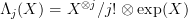
    where a structure of this species is a set S together with a decomposition S = S_1 + S_2, where S_1 carries the structure of being a j-element set (structure of species X^j/j!) and S_2 carries the structure of being just a set (structure of species exp(X)).

    It sounds as though you were describing your instinct as saying that all finitary species are generated by sums and products of the L_j (here, the 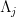\Lambda_j I guess). Possibly I have misunderstood. But it sounds like you were therefore hinting at a characterization of atomic species, which as far as I know is a difficult problem. There is some discussion of this in the book by Bergeron, Labelle, and Leroux: Combinatorial Species and Tree-Like Structures (Encyclopedia of Mathematics and its Applications 67, Cambridge University Press, 1998).

    • CommentRowNumber7.
    • CommentAuthorTobyBartels
    • CommentTimeNov 1st 2009

    Is this in the Lab?

    • CommentRowNumber8.
    • CommentAuthorTodd_Trimble
    • CommentTimeNov 1st 2009

    Is what in the Lab?

    • CommentRowNumber9.
    • CommentAuthorTobyBartels
    • CommentTimeNov 1st 2009

    I mean the stuff that you introduced with ‘Since there may be other people looking on, I'm going to add some words I used to explain some of this to myself’. I don't think that we even have an article on the trace of a category yet, but much of what you wrote could go on such a page. You're right that others are watching, and I was looking for a place to put it so (as Urs would say) it won't get lost.

    • CommentRowNumber10.
    • CommentAuthorTodd_Trimble
    • CommentTimeNov 1st 2009

    No, not much of it is there yet; in particular, there's no trace of a category written up, and some of the articles surrounding species may be a little dry and could use some freshening up with examples of calculations like some of the ones here (there are some beautiful calculations in the original article by Joyal).

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeNov 2nd 2009
    I agree with Toby, we should try not to be typing too much useful stuff into comment boxes here without keeping a copy in a suitable nLab entry. And be it in a query box.

1 to 11 of 11

  1.