nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeOct 30th 2009
- (edited Oct 30th 2009)
After creating Understanding M-Set, I was tempted to start an "Understanding Set", but then there are other categories I'd like to understand as well.
This gave me an idea of starting a series of "Understanding"s. The idea is to take a category and work through standard constructions in gory details, e.g. products, coproducts, general limits and colimits, etc. We could make a laundry list of standard constructions that go with a category and work them out in detail.
What do you think?
As a start, it might be good to go ahead and work through everything for Set. The idea is to help (me!) understand all this stuff.
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeOct 30th 2009
Yeah, I could do that with you. We could start at Set, but if it gets long move it to category-theoretic constructions in Set or even understanding Set if you like.
Understanding
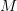 -
-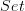 is the title of a reference; if you want a reference for understanding
is the title of a reference; if you want a reference for understanding 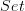 , perhaps we could work through Sets for Mathematics (by Lawvere & Rosebrugh).
, perhaps we could work through Sets for Mathematics (by Lawvere & Rosebrugh). -
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeOct 30th 2009
- (edited Oct 30th 2009)
Cool. Maybe we can make a list of desired constructions here?
- Products
- Coproducts
- Limits
- Colimits
- Etc
I kind of like the idea of having a "series" with a friendly name like "Understanding Set", "Understanding Top", etc even if it happens to conflict with an actual reference. We can just note the reference on the page.
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeOct 30th 2009
As long as the series name is downcase (understanding Set), then it won't conflict with the reference. Or constructions in Set, constructions in Top, etc; I just realised that ‘category-theoretic’ is redundant when we're discussing categories! On the other hand, if you can get a copy of Lawvere & Rosebrugh (which is published as a paperback book), then that would give some structure to the discussion, if you like it.
Under limits:
- terminal object
- binary products
- arbitrary (but small) products
- equalisers
- pullbacks
- fibred products
Under colimits:
- coterminal object
- binary coproducts
- arbitrary (but small) coproducts
- coequalisers
- pushouts
- cofibred coproducts
Other constructions:
- exponential objects
- dependent products
- power objects
- probably more
-
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeOct 30th 2009
<div> <p>Cool! Thanks.</p> <blockquote> As long as the series name is downcase (understanding Set), then it won't conflict with the reference. </blockquote> <p>But this <i>is</i> a reference. References should be capitalized. If there is already a called "Understanding Set", then we can just add a reference to that reference on the page. While you were typing your comment, I created</p> <ul> <li><a href="https://ncatlab.org/nlab/show/Understanding+Categories">Understanding Categories</a></li> <li><a href="https://ncatlab.org/nlab/show/Understanding+Set">Understanding Set</a></li> </ul> <p>"Constructions on Set" is good too, but doesn't sound as "friendly" as I was hoping. How about "Understanding Constructions on Set"?</p> </div> -
- CommentRowNumber6.
- CommentAuthorJonAwbrey
- CommentTimeOct 30th 2009
Too bad The Joy of Sets is already taken …
-
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeOct 30th 2009
I liked "Understanding Constructions" so renamed the pages.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
- (edited Oct 30th 2009)
Great idea.
Something along these lines we tried to establish before, at limits and colimits by example.
be sure not to forget to link from Set to Understanding Constructions on Set!
Ah, and I would suggest it should be "Construction in Set" (in the category of all sets) .
-
- CommentRowNumber9.
- CommentAuthorEric
- CommentTimeOct 30th 2009
Ok. Great. Would it also be "in Categories"? I'll change it to "in Set".
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
Yes, I think what you are looking for is "Constructions in Categories".
I would read "Constructions on Categories" as being the same as "Constructions in Cat" !
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeOct 30th 2009
Thanks. Done :)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
- (edited Oct 30th 2009)
Jon, this is so boring. We asked you several times to stop it. Who are you doing this for? You are creating background noise, and nobody but you is enjoying it. Please stop.
-
- CommentRowNumber13.
- CommentAuthorTobyBartels
- CommentTimeOct 30th 2009
@ Eric
But this is a reference.
What reference? I don't know any papers or books with these titles, and it's even worse if there are any, since we're not going through them. If you mean that we're writing our own reference, how is that different from any other page on the Lab?
@ Urs
Complaints about Jon's silly puns are noisier than the puns themselves, IMHO. (Actually it's not his pun this time, but Keith Devlin's.)
-
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeOct 30th 2009
I think pages on the nLab can be categorized into at least two different categories (terminology overload!). Dictionary or encyclopedia type pages, e.g. category, which are lower case and "articles" about pages or even articles about other articles. I think articles should have article titles with proper capitalization. For example,
geometric infinity-function theory
should be capitalized, in my opinion, like An Exercise in Kantization.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
- (edited Oct 30th 2009)
I think we mostly capitalized if the title of the entry is actually the title of some existing document. While it is true that the entry geometric infinity-function theory is about an existing document, the entry title isn't the title of that document. So this is maybe a boundary case.
But i'd be happy to capitalize this entry's title. That would also give me the chance to later create a lower case page on geometric oo-function theory with a FULL theory of geoemtric oo-functions, not restricting to the algebraic site.
-
- CommentRowNumber16.
- CommentAuthorEric
- CommentTimeOct 30th 2009
Maybe you could call it "Understanding Geometric Infinity-Function Theory" :)
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
I wish it were.
My attempt to make "journal club" members work through details and questions in that entry in the spirit of your "Understanding xyz"-series pretty much failed.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeOct 30th 2009
Maybe we should have a blog post about the Understanding-Set entry? Inviting people to participate and discuss matters there?
-
- CommentRowNumber19.
- CommentAuthorTobyBartels
- CommentTimeOct 31st 2009
I still want a lowercase title, but I'm not too picky now.
I was thinking of asking you a bunch of questions, Eric, but you've already asked some of them. Should I provide the answers?
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeOct 31st 2009
@Urs: Sounds like a good idea, but maybe we can fill in some more content so that it is "mostly" done. That way it can act as a model for other "Understandings". For example, once people see how Set is done, it should be fun to fill in Top. Inviting people to look at and fill in a mostly empty page will probably lead to disappointing results.
@Toby: Please feel free to add anything you want :)
-
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeNov 1st 2009
OK, I've added a thorough (I hope!) description of nullary and binary products. I left the arbitrary products as an exercise for you.
-
- CommentRowNumber22.
- CommentAuthorAndrew Stacey
- CommentTimeNov 2nd 2009
I'd just like to say that I think that this is a great idea.
And make sure that these pages are linked from the database of categories.
-
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeNov 2nd 2009
@ Andrew
So linked (at least for Understanding Set).
-
- CommentRowNumber24.
- CommentAuthorEric
- CommentTimeNov 2nd 2009
- (edited Nov 3rd 2009)
Thanks for getting the ball rolling Toby. With your help, I'm starting to see a pattern emerge on Understanding Constructions in Set.
- Remind what a universal cone is in the particular category (currently Set)
- State how each construction is a universal cone over a special diagram
- Give the answer for what each construction corresponds to for each diagram in the particular category
- Explain how things work.
-
- CommentRowNumber25.
- CommentAuthorEric
- CommentTimeNov 4th 2009
In a category of cones, the limit (if it exists) is an object. Is it a terminal object or something? It would be neat if we could say "A limit is a terminal object in the category of cones." Is that correct?
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeNov 4th 2009
Yes, that's correct. The "limiting cone" is the terminal cone: every other cone has a unique cone morphism into it.
Analogously for colimits: the "colimiting co-cone" is the initial co-cone.
(If they exist.) -
- CommentRowNumber27.
- CommentAuthorEric
- CommentTimeNov 4th 2009
Neat. Thanks! I think I am starting to "Understand" :) I'll pass on to the nLab whatever knowledge I manage to get through my thick skull :)
-
- CommentRowNumber28.
- CommentAuthorEric
- CommentTimeNov 5th 2009
- (edited Nov 5th 2009)
The material just on "limits in Set" was enough to create a separate page, so I did:
It would be great if an expert could have a look and see if I've made any glaring errors. Of course, improvements are always welcome (and needed)!
PS: This has been a really good exercise for me personally.
1 to 28 of 28