Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: regular epimorphisms

Bottom of Page

1 to 33 of 33

  1.  
    • CommentRowNumber1.
    • CommentAuthorMike Shulman
    • CommentTimeNov 4th 2009

    Comment/question on terminology in the (?,1)-case at regular epimorphism

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeNov 4th 2009
    this relates to a discussion Toby and I had back then. Have you looked at the query box at effective epimorphism?
    • CommentRowNumber3.
    • CommentAuthorMike Shulman
    • CommentTimeNov 4th 2009

    Yes, that's what prompted me to think about it. It looked to me as though your discussion was just about where to draw the line between "regular" and "effective," though, rather than whether the word "epimorphism" is warranted -- was I wrong?

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeNov 4th 2009
    • (edited Nov 4th 2009)
    Ahm, I will have to remind myself. This discussion was driven by Toby, I just tried to react, so he likely thought about it more deeply than I ever did. I'll try to get back to this later when I have a spare minute to think about it...
    • CommentRowNumber5.
    • CommentAuthorTobyBartels
    • CommentTimeNov 5th 2009

    It never occurred to me that they might not actually be epimorphisms.

    I now officially wish even more than ever that the term ‘epimorphism’ had originally been used (in category theory) for regular epimorphisms (with ‘comonomorphism’ —or anything else, really— for arbitrary epimorphisms). First for stepping over the algebraists' usage, and now this! If only I had a time machine …

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeNov 5th 2009
    Now I had a minute and started looking into this again. Nothing substantial yet, but I did something:

    I expanded the first part of effective epimorphism. I added the statement that a morphism is effective epi precisely if it is its own coimage.

    (That's kind of curious, isn't it? Maybe image and coimage were named the wrong way round?)
    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeNov 5th 2009
    • (edited Nov 5th 2009)
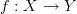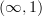    one general concept that should make sense to consider is that of morphisms f : X \to Y in an (\infty,1)-category 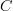C such that for every other object 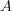A we have that the induced morphism of oo-groupoids 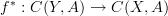f^* : C(Y, A) \to C(X,A) is a full and faithful (infinity,1)-functor .

    But Mike says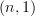 (n,1) -functors with simplicial resolution may fail to be of this kind already for 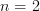n=2 . Hm...
    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeNov 5th 2009
    • (edited Nov 5th 2009)
    Wait, I am maybe confused about your comment, Mike: in your notation hom(B,X) and hom(A,X) are 1-groupoids for the ambient thing a (2,1)-category. So you mean "surjective on 2-cells" instead of "injective on 2-cells". Is that right?
    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeNov 5th 2009
    One thought:

    we can reduce this problem to asking the following:

    how are homotopy limits of simplicial sets over cosimplicial diagrams characterized?

    Because that's what characterizing regular (oo,1)-morphisms following Toby's suggesion boils down to:

    this is asking for the characterization of colimits over simplicial diagrams in any (oo,1)-diagram. For every other object, homming this colimit into that object produces a limit of oo-groupoids over a cosimplicial diagram. In the 1-categorical case this limit is an equalizer and hence yields a monomorphism. Now we want to say what happens for general homotopy limits over cosimplicial diagrams.

    I still don't know the answer, but I thought I mention the idea that this might be the fundamental question to look at.

    But on the other hand, Toby's implicit suggestion that one should _define_ epimorphism in an (oo,1)-category as "regular epimorphism"="morphism with simplicial resolution" sounds to me like it might well be the only "right" answer in the end.

    You can also read this between the lines in Lurie's book where he starts talking about effective epimorphisms. He effectively argues that the only thing that matters in practice is whether there is a simplicial resolution or not.
    • CommentRowNumber10.
    • CommentAuthorTobyBartels
    • CommentTimeNov 5th 2009

    Toby's implicit suggestion that one should define epimorphism in an (oo,1)-category as "regular epimorphism"

    I'd be hesitant to do this now, since it would conflict with the standard definition of ‘epimorphism’ for 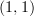(1,1)-categories. (In particular, I would not want to do this for (\infty,1)-categories unless I also did this for categories —and you can see how dangerous that would be!) It's just that, if I a time machine, I'd go back and convince people to change that from the very beginning.

    On the other hand, I'd say to go ahead and use the term ‘regular epimorphism’ anyway; just throw out a warning that such a thing might not be an epimorphism, except in low dimensions.

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeNov 5th 2009

    Okay, I put in a warning. Have a look.

    • CommentRowNumber12.
    • CommentAuthorGuest
    • CommentTimeNov 6th 2009
    I'm not surprised that there isn't a good version of a standard epimorphism in an (oo,1)-cat, as the naive notion in Top is not really a nice sort of map. There one (i.e. me) uses maps that are epimorphisms under the Yoneda embedding Top --> Sh_J(Top) for some topology J on Top. I call these J-epimorphisms. I have no idea how to extend this to arbitrary (oo,1)-cats, as Top is of course special, with its underlying category structure. Perhaps any (oo,1)-category associated to a category with interval can be treated in the same way? I think at the very least one would want the map X^I --> X x X to be a J-epi for path-connected X. Note however that this fails for Top with the standard path space and the pretopology of open covers when considering arbitrary spaces - it only holds for locally contractible spaces (in the weaker sense). If J is the pretopology of open surjections, X^I --> X x X is a J-epi for all locally connected X. Certainly there is much to think about, even for such a well-known situation.

    -David Roberts
    • CommentRowNumber13.
    • CommentAuthorMike Shulman
    • CommentTimeNov 6th 2009

    @Urs: when I said "injective on 2-cells" I meant "injective on the 2-cells in your (2,1)-category", which of course means injective on the 1-cells in the hom-groupoids (which is of course the same as surjective on 2-cells in those 1-groupoids). That was poorly phrased, sorry about that.

    I'm okay with using "regular epi" for this notion, as long as the reader is warned.

    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeNov 6th 2009

    Okay. For completeness I added an analogous discussion at regular monomorphism. I also slightly expanded regular epimorphism.

    • CommentRowNumber15.
    • CommentAuthorzskoda
    • CommentTimeMay 15th 2011
    • (edited May 15th 2011)

    At regular coverage we have now:

    For a regular category CC, the regular coverage on CC is the coverage whose each covering family has one element which is a regular epimorphism.

    The Grothendieck topology generated from a regular coverage is called the regular topology.

    subcanonical Grothendieck topology whose covering families are generated by single regular epimorphisms: the regular coverage.

    I started cleaning that but then I noticed that this paragraph is a mess semantically. I mean if we say

    the coverage whose covering families consist of single regular epimorphisms.

    then there are MANY such topologies whose covering families satisfy that criterion. But “the” wants maybe to have the maximal coverage of that type, that is that it is

    the coverage whose covering families are all families consisting of a single regular epimorphism.

    The second sentence however says “generated from a regular coverage” what additionally confuses. I am also used to the term “the regular epimorphism topology” when talking about the maximal one.

    Edit: An additional point is at regular epimorphism. It says there in idea section that regular epimorhism is something like the covering. This is quite misleading. Namely, there exist Grothendieck pretopologies which are not subcanonical. If the category if regular then the pretopology is subcanonical (and of course singleton pretopology) iff it consists of regular epis. If the category is not regular, then I think strict or strong epi is closer (David Roberts will say more precise) to the “subcanonical” condition than regular. In any case, I perceive that having all coverings singleton regulars is closer to being subcanonical then to be just a covering while even this is not precise.

    P.S. I added definitions of classes of epis under epimorphism at variations sections. I mean it was difficult to read so many implications without having all definition ready (i.e. not going back and forth to many linked pages).

    One of the epimorphism pages says that a regular epimorphism is split in SetSet with axiom of choice. So the same in every Grothendieck topos, right ?

    • CommentRowNumber16.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 16th 2011

    Hi Zoran,

    one can take the largest class of regular epimorphisms which is stable under pullback and this will be the subcanonical singleton pretopology. In general, though, the regular epis entire don’t form much.

    Personally I would like to define a singleton pretopology as a high-level concept - it is a wide subcategory containing all isomorphisms, and such that the arrows are stable under pullback in the full category. Then one can talk about the regular pretopology in a much simpler way, as well as other singleton pretopologies whose covering families consist of classes of epimorphisms of varying ’strength’.

    Every epi in a pretopos is regular, so one only has epis and split epis. AC is precisely when these two classes coincide.

    • CommentRowNumber17.
    • CommentAuthorzskoda
    • CommentTimeMay 16th 2011

    Right, thanks for reminding me (for “stable under pullbacks” i.e. universal regular epimorphisms). But is it the class of universal regular epis the same as the class of universal strict epis ? (I should take a couple of minutes thought, but now I am in a hurry and ask instead :)). I am mainly interested in non-topos situation.

    • CommentRowNumber18.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 16th 2011

    Hmm. Not sure. I’ll have a think while on the plane tomorrow to Melbourne (hurrah for work-paid flights!)

    • CommentRowNumber19.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 16th 2011

    At strict epimorphism we see that if your category has pullbacks, then strict epi = regular epi. Without pullbacks (eg DIff) I don’t know yet.

    • CommentRowNumber20.
    • CommentAuthorzskoda
    • CommentTimeMay 16th 2011
    • (edited May 16th 2011)

    Yes, I know that. The question is which version works more generally, when they differ.

    Edit: I see that people misunderstood my statement above. I did not ask which class of morphisms is more general, that is easy and listed at epimorphism at the place which I edited yesterday ! I asked which of the conditions on epis is more appropriate for the guarantee that the singleton pretopology is subcanonical in more general situations in which regular, strong and strict differ.

    • CommentRowNumber21.
    • CommentAuthorTobyBartels
    • CommentTimeMay 16th 2011

    @ Zoran #17: Yes, they are the same. The argument (that, in category with pullbacks, every strict epimorphism is regular) also serves to prove that any universal strict epimorphism is regular (hence universal regular). More than that, as long as a strict epimorphism has all pullbacks (regardless of whether these pullbacks are also epic), then it has a kernel pair and hence (being the coequaliser of this kernel pair) is regular.

    • CommentRowNumber22.
    • CommentAuthorzskoda
    • CommentTimeMay 16th 2011
    • (edited May 16th 2011)

    (Again, I know that.) Edit:sorry, I did not know the part about universal, I misread your answer (I just knew the relations between strict strong and regular as in epimorphism). Thanks Toby.

    The question was which natural/largest class of epimorphisms on a general category has the property that if a singleton Grothendieck topology is made from some subclass of that class then it is automatically subcanonical. Or the best approximation to the answer. Thus when the strict and regular epimorphisms differ what is the right choice. Some people say strong, some strict and some regular…

    • CommentRowNumber23.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 16th 2011

    universal strict epimorphisms ⊂\subset universal regular epimorphisms by #21, so any singleton pretopology consisting of universal strict epis is subcanonical. For subcanonical all you need is that the arrows are a subclass of the regular epimorphisms.

    • CommentRowNumber24.
    • CommentAuthorzskoda
    • CommentTimeMay 16th 2011

    Also my complaints about the idea section of regular epi stay.

    In a topos regular epimorphism topology is of course having a special natural role, but then this is a stemement on the topology consisting of all regular epimorphism singletons, not about the idea of a single regular epimorphism in a general category. So I disagree with an Idea section and also with entry covering. If one wants to have some idea about the regular epimorphism pretopology then there is the entry regular epimorphism suited for that (and my understanding is that some a vs. the articles there are incorrect but I do not quite understand the intention of the idea section so I did not edit. Finally I think that regular/strong/strict epi condition when they are the same make the pretopology consisting of SOME such epimorphisms subcanonical.

    The second line of the idea section of covering

    effective monomorphism ⇒ regular monomorphism ⇔ embedding

    again needs a context. Grothendieck school takes (morphisms of presheaves represented by) strict monomorphisms for the abstract definition of a closed immersion of algebraic spaces viewed as sheaves of sets.

    • CommentRowNumber25.
    • CommentAuthorzskoda
    • CommentTimeMay 16th 2011
    • (edited May 16th 2011)

    I see in the meantime when I was writing the above entry, David’s answer appeared. David thanks. You are saying that precisely regular guarantees the pretopology to be subcanonical without any additional assumptions on the category ?

    • CommentRowNumber26.
    • CommentAuthorMike Shulman
    • CommentTimeMay 17th 2011

    I think that really essentially by definition, a singleton coverage is subcanonical iff it consists of strict epis, hence a fortiori if it consists of regular ones. (In the world of Grothendieck topologies, strict epimorphic families are more commonly called effective ones.) If those strict epis actually have honest pullbacks, then Toby’s argument implies that they must necessarily be regular.

    Re: AC, it may be worth remembering that there is also the “internal AC” in a topos, which does not imply that all epis are (externally) split, only that they are “locally” split.

    • CommentRowNumber27.
    • CommentAuthorGuest
    • CommentTimeMay 17th 2011

    Hi Zoran #24 - I also don’t like the generic term ’covering’, which I think comes from the Elephant.

    25 A singleton pretopology is subcanonical if every covering map is effective, and this is the same as it being a regular epimorphism as Mike says. Add pullback stability = universal (blah) epimorphism, then you have a subcanonical pretopology. If you have all the universal regular epis then you have the canonical singleton pretopology.

    David (from Melbourne airport)

    • CommentRowNumber28.
    • CommentAuthorzskoda
    • CommentTimeMay 17th 2011
    • (edited May 17th 2011)

    Mike thanks. David: Mike suggests that if we translate the definitions it is strict epi which is the necessary condition, not necessarily regular. That is what I wanted to hear. So all universal strict epis forms canonical in general category I guess.

    • CommentRowNumber29.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 18th 2011

    Ah, yes. I was thinking of working with a Grothendieck pretopology, not a coverage (i.e. only weak pullbacks exist). In that case I agree that strict epis would be the better notion.

    And I apologies for the massive SHOUTING in #27 - I didn’t preview my post and something got a bit weird with a # symbol somewhere. I can’t edit it now…

    • CommentRowNumber30.
    • CommentAuthorTobyBartels
    • CommentTimeMay 18th 2011

    You can’t edit it since you weren’t logged in when you made it; and the weird bit is that you began a line with #.

    • CommentRowNumber31.
    • CommentAuthorDavidRoberts
    • CommentTimeMay 18th 2011

    @Toby Yeah, I know. I was trying for

    #25 blah blah

    but of course it didn’t format how I expected.

    • CommentRowNumber32.
    • CommentAuthorzskoda
    • CommentTimeMay 20th 2011

    I see there is an old query under Morita equivalence mentioning regular epis

    So is it true that there is a model category structure on algebras such that Morita equivalences of algebras are spans of acyclic fibrations with respect to that structure?

    Zoran Škoda: Associative (nonunital) algebras make a semi-abelian category, ins’t it ? So one could then apply the general results of van den Linden published in TAC to get such a result, using regular epimorphism pretopology, it seems to me. It is probably known to the experts in this or another form.

    • CommentRowNumber33.
    • CommentAuthorTodd_Trimble
    • CommentTimeJun 16th 2017

    In accordance with a discussion yesterday, I added an example at regular epimorphism showing that regular epis need not be closed under composition.

1 to 33 of 33

  1.