nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
Fixed the comments in the reference list at model structure on dg-algebras: Gelfand-Manin just discuss the commutative case. The noncommutative case seems to be due to the Jardine reference. Or does anyone know an earlier one?
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I have a question at model structure on dg-algebras on the invariant characterization of commutative dg-algebras within all dg-algebras.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I added an "Idea" section to model structure on dg-algebras
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
- (edited Nov 11th 2009)
I added a theorem from the book by Igor Kriz and Peter May about how commutative dg-algebras already exhaust, up to weak equivalence, all homotopy-cmmutative dg-algebras to model structure on dg-algebras.
(this might better fit into some other entry eventually, though)
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
Added the statement that the forgetful functor from commutative dg-algebras to all dg-algebras is the right adjoint part of a Quillen adjunction with respect to the given modelstructures.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeNov 11th 2009
I would look into Hinich's 1995 or so paper, for a possible earlier reference. -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
- (edited Nov 12th 2009)
created a section on cofibrations in CdgAlg and hence on Sullivan algebras.
Created entry for Dennis Sullivan in that context. Always nice to create an entry and see that the "timeline"-entry was already requesting it.
I suppose I'll have the following sorted out in a minute, but maybe somebody is quicker with helping me:
in the definition of a relative Suillvan algebra
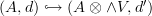 I suppose we do require that
I suppose we do require that 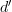 restricted to
restricted to 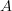 acts like
acts like 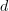 plus a term that contains elements in V ?
plus a term that contains elements in V ? -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeNov 29th 2010
I started at model structure on dg-algebras a new subsection on Unbounded dg-algebras, stating a basic existence result.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeDec 9th 2010
added a section Simplicial hom-objects to model structure on dg-algebras on the derived hom-spaces for unbounded commutative dg-algebras (over a field of char 0).
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeDec 9th 2010
- (edited Dec 9th 2010)
okay, I think I finally have assembled the full proof that the derived copowering of undbounded commutative dg-algebras (over field of char 0) over degreewise finite simplicial sets is given by the polynomial-differential-forms-on-simplices-functors. I have written this out now at Derived powering over sSet.
This provides the missing detail for the discussion that 𝒪(S1)≃k⊕k[−1] over at Hochschild cohomology. This is supposed to be all very obvious, but it took me a bit to assemble all the details properly, anyway.
I now moved other discussion of the model structure on commutative unbounded dg-algebras from the Hochschild entry over to model structure on dg-algebras. This mainly constituting the other new section Derived co-powering over sSet.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
I added statement and proof that ([n]↦Hom(A,B⊗Ω•poly(Δ[n]))) is a Kan complex when A is cofibrant.
Also added an earlier reference by Ginot et al where it is discussed that their “derived copowering” of cdgAlg over sSet indeed lands in commutative dg-algebras. I’ll try to add more technical details on how this works later on.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJul 16th 2014
- (edited Jul 16th 2014)
there was an old question of how (to which extent) the homotopy theory of commutative dg-algebras is homotopy-faithful inside that of all dg-algebras.
Recently there appeared some discussion of this issue in
Ilias Amrani, Comparing commutative and associative unbounded differential graded algebras over Q from homotopical point of view (arXiv:1401.7285)
Ilias Amrani, Rational homotopy theory of function spaces and Hochschild cohomology (arXiv:1406.6269)
I have added pointers to this here.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeFeb 21st 2017
- (edited Feb 21st 2017)
I have added to the section on the Bousfield-Gugenheim model structure a subsection on its simplicial hom-complexes which almost but not quite, make for a simplicial model category structure.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeAug 19th 2020
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeAug 19th 2020
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeAug 21st 2020
- (edited Aug 21st 2020)
Added full publication data to:
- Paul Goerss, Kirsten Schemmerhorn, Model categories and simplicial methods, Notes from lectures given at the University of Chicago, August 2004, in: Interactions between Homotopy Theory and Algebra, Contemporary Mathematics 436, AMS 2007(arXiv:math.AT/0609537, doi:10.1090/conm/436)
Around Example 3.7, these authors make (somewhat implicitly) the observation that the Bousfield-Gugenheim model structure on connective rational dgc-algebras (which B&G and later Gelfand&Manin establish by laborious checks) is simply that right transferred from the projective model structure on chain complexes – which makes the proof that relative Sullivan models are cofibrations a triviality.
So this is all very nice, and highlighted as such in Hess’s recview. But neither of these authors states this as a theorem that could be properly cited as such, instead they leave it at side remarks. Is there any author who has published this in more citeable form?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeAug 23rd 2020
added paragraph on the Quillen adjunction between simplicial sets and connective dgc-algebras
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeSep 1st 2020
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJul 7th 2021
-
- CommentRowNumber20.
- CommentAuthorTodd_Trimble
- CommentTimeJul 11th 2021
Changed ℝ to k.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJul 11th 2021
Ah, right. Thanks.
1 to 21 of 21