Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Discussion Tag Cloud

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Bayesian update of a category

Bottom of Page

1 to 13 of 13

  1.  
    • CommentRowNumber1.
    • CommentAuthorBen_Sprott
    • CommentTimeMar 25th 2012
    • (edited Mar 25th 2012)

    I recently discovered an nlab articleon categorified probability theory. It features my old advisor as the central reference. I have been trying to put a finger on a concept I call “category update”. This “category update” is meant to capture the notion of Bayesian update when we are using a category as a model rather than a probability space. A typical update would be to add a morphism to a category, or to conclude that two morphism can be composed. Thus a category update is a functor f:C→C ′f : C \rightarrow C^{\prime}. At this point, I don’t know what properties I want the functors to have as I only have an intuition of what “update” means. Regardless, I am going to assume that this “update” is a categorification of Bayesian inference. This assumption allows me to start by looking at a category of probability spaces as a place to begin categorifying Baye’s rule. Clearly, in a category of probability spaces, Bayes rule is a morphism and the question is whether or not it is the most general morphism. If it were, this would mean that the category of probability spaces is a category with probability spaces as objects and Bayesian inference as morphisms. Now looking at the nlab article, we see that Panangaden chooses conditional probability densities as morphisms which looks something like Bayes rule. Regardless, what i am interested in is n-ifying this by exactly one layer in that I want to exchange the probability spaces for categories. A question might be, once we have done this and we have some collection of categories with updates between them (functors of special nature) what can we say about this collection? For instance, it must be a category, but what rules will the morphisms obey? What, if any are the axioms of the category?

    • CommentRowNumber2.
    • CommentAuthorTobyBartels
    • CommentTimeMar 25th 2012

    [Discussion moved to the Atrium.]

    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeMar 25th 2012

    A typical update would be to add a morphism to a category, or to conclude that two morphism can be composed.

    If the latter is done without evil, then it’s a special case of the former; to conclude that a:u→va\colon u \to v and b:x→yb\colon x \to y can be composed (to produce a;ba ; b, or b∘ab \circ a), we add an isomorphism h:v→xh\colon v \to x. (That’s really adding two morphisms and two equations between composable morphisms.)

    Thus a category update is a functor f:C→C′f\colon C \rightarrow C'. At this point, I don’t know what properties I want the functors to have as I only have an intuition of what “update” means.

    If it’s no more general than your typical updates above, we would want to say that C′C' (up to equivalence) is just CC with extra morphisms (and equations between morphisms) but not extra objects. So we would require ff to be essentially surjective. Does this seem reasonable?

    • CommentRowNumber4.
    • CommentAuthorDavid_Corfield
    • CommentTimeMar 25th 2012

    Clearly, in a category of probability spaces, Bayes rule is a morphism…

    How does this work?

    • CommentRowNumber5.
    • CommentAuthorBen_Sprott
    • CommentTimeMar 25th 2012
    • (edited Mar 25th 2012)
    Hi Toby,

    I was hoping my functors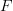 F would be more general allowing us to add arbitrary objects. I mean, if we add two morphisms 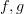f,g and no extra axioms,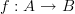

    f : A \rightarrow B
    g : C \rightarrow D

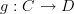
    doesn't this require the objects to have no extra data too, ie not to be isomorphic? Having said that, I have no intuition here. I guess I was hoping that if we understood Baye`s rule in a category of probability spaces (assuming that it even is a morphism), then it would give us more data about our functors.

    Hi David,

    Thanks for your question. I might be wrong about how Baye's rule is a morphism. We know that Baye's rule maps a probability space to a probability space. That's all I am working on really. Thus, in a category of probability spaces, Baye's rule is a morphism. Your question is precisely what I am trying to figure out. How do we take Baye's rule and turn it into a morphism in an appropriate category. There are two possibilities. The first is that Baye's rule is the most general map and thus it defines a category. The second is that it is some special case of a map in some category. Maybe we can just start by understanding a category of probability spaces.

    I tried working out general morphisms given a probability space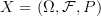
    X= ( \Omega, \mathcal{F}, P)
    and got to a typical point where we define a map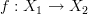
    f : X_{1} \rightarrow X_{2}
    as a morphism in Prob, the category of probability spaces and “their structure preserving maps”. We do this in a standard way.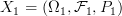

    X_{1}= ( \Omega_1, \mathcal{F}_1, P_1)
    X_2= ( \Omega_2, \mathcal{F}_2, P_2)

    f : \Omega_1 \rightarrow \Omega_2

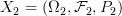
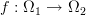
    We take the axioms for the sigma algebra in a very algebraic tone.
    Complements:
    Let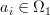
    a_i \in \Omega_1
    b_i \in \Omega_2,

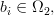
    Given that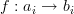
    f: a_i \rightarrow b_i,
    where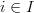
    i \in I and
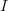    I is countable then we enforce that following about restricted maps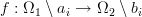

    f: \Omega_1 \setminus a_i \rightarrow \Omega_2 \setminus b_i

    where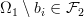

    \Omega_1 \setminus b_i \in \mathcal{F}_2

    Countable unions: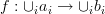

    f: \cup_i a_i \rightarrow \cup_i b_i

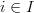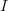    where i \in I, and I is countable and \cup_i b_i \in \mathcal{F}_2.

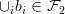    Next we would have to have axioms about $P_1$ and I didn't know what to do there.
    • CommentRowNumber6.
    • CommentAuthorTodd_Trimble
    • CommentTimeMar 25th 2012

    Argh! It’s Bayes, not Baye. The possessive form ought to be Bayes’s (my preference), or Bayes’, but definitely not Baye’s!

    • CommentRowNumber7.
    • CommentAuthorBen_Sprott
    • CommentTimeMar 26th 2012

    Heh, sorry! Todd has helped a lot in the past and is certainly no stranger to having to be patient with me. Bayses's it is!

    • CommentRowNumber8.
    • CommentAuthorTodd_Trimble
    • CommentTimeMar 26th 2012

    Bayses’s it is!

    Thanks for making me laugh! :-)

    • CommentRowNumber9.
    • CommentAuthorTim_Porter
    • CommentTimeMar 26th 2012

    Just a thought from a very much NON-expert on this, might the idea of working with presentation of the categories, and eventually with polygraphs or computads help here. The idea of adding morphisms and / or objects reminds me of constructions from simple homotopy theory where new cells are added in definite ways. (Cf. also Morse theory).

    Going back to the original post, Ben suggested update ’to conclude that two morphism can be composed’, but that requires equality of two ‘points’ to be proved, and equality is not a nice thing (see Toby in #3). This will otherwise form a quotient.

    • CommentRowNumber10.
    • CommentAuthorBen_Sprott
    • CommentTimeMar 27th 2012
    • (edited Mar 27th 2012)
    Hi Tim,

    Thanks for the feedback!
    I used the word conclude, as in "one concludes that two morphisms are equal", not in any strict sense. You put your finger closer to the idea with the mention of presentations. We are eschewing a strong notion of a concrete reperesentation of our updatable categories in favour of the presentation of such cats. Words like "data" are used to evoke this. Updatable categories could each be presented as a list (data) of morphisms and a list of equations over the morphisms. These lists are finite for only some of the categories in the category that I alluded to: C, categories as objects and updates as morphisms. The cats with finite lists are probably going to turn out to be compact or finitely presentable. Something tells me that we want to have both finitely and not-finitely presentable cats in C, and this can tell us more information about what an "update" is.
    • CommentRowNumber11.
    • CommentAuthorTim_Porter
    • CommentTimeMar 27th 2012

    Ben,

    have you looked at persistent homology as used by Gunnar Carlsson and others. There one has an ’evolving’ simplicial complex indexed, in the simplest form, by real numbers. If you pass to the associated poset of simplices then it gives, it seems to me, a good example of an updatable or evolving category which is highly controllable, but I am not sure it is what you want. Have a look.

    • CommentRowNumber12.
    • CommentAuthorBen_Sprott
    • CommentTimeMar 29th 2012
    • (edited Mar 29th 2012)

    Hi Tim,

    I want to thank you for your input. I will look into the poset of simplices. I have advocated in the past for a dcpo of partial monoids as a nice setting for reasoning about structure. The partial monoids are the arrow and equation presentation that I mentioned. Your suggestion, I feel, is to imbue the presentation with some geometry, to get the simplex, and reason geometrically. Though you then mention the poset of simplexes so maybe youu feel the ordered structure, much like a dcpo, is the appropriate place to reason. In any case, this is very exciting and I will see how far I get.
    Thanks again.

    • CommentRowNumber13.
    • CommentAuthorTim_Porter
    • CommentTimeMar 29th 2012
    • (edited Mar 29th 2012)

    My POV is that the evolving simplicial complex (or similar) may be more directly useful initially b=ut you were asking for some sort of evolving category and the poset given by the abstract simplicial complex may give you an example of such. There is another related idea which used the relationship between finite topological space (T_0 ones at least) and posets. This allows a bit more freedom for the pictures you get but I suspect is somehow equivalent.

    Another important point coming from those examples (structures from Persistent homology and topological data analysis) is that both structure evolves quite naturally at several different levels, yet the situations leading to this are quite simple to motivate and describe.

    I have this dream of applying that sort of technology, suitably adapted, to causality, as well as to modal logics, heigh ho! too much to do. :-)

1 to 13 of 13

  1.