nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
- (edited Nov 16th 2009)
Created elementary embedding to record a proof that I learned from Nate Ackermann. The upshot is that Kunen's technical argument for the inconsistency of an e.e.
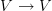 , and its use of choice, is unnecessary if you merely care about definable e.e.'s.
, and its use of choice, is unnecessary if you merely care about definable e.e.'s. -
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
And created large cardinal as a stub, mostly so that elementary embedding wouldn't be an orphan.
-
- CommentRowNumber3.
- CommentAuthorDavid_Corfield
- CommentTimeNov 16th 2009
Are these embeddings the same as those we spoke about in the Fraisse limits post, or is 'elementary' qualifying somehow? -
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
The embeddings we used for Fraisse limits were only required to preserve and reflect the truth of atomic statements, rather than all first-order statements.
-
- CommentRowNumber5.
- CommentAuthorDavid_Corfield
- CommentTimeNov 16th 2009
Thanks. Would it be worth a page differentiating types of embedding - geometric, Yoneda? Or isn't there enough in common to merit such a page? -
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
Couldn't hurt, I think.
-
- CommentRowNumber7.
- CommentAuthorjesse
- CommentTimeMay 27th 2017
- (edited May 27th 2017)
I’ve formalized Urs’ observation from seven(!) years ago that an elementary embedding is a natural transformation, under Proposition 4.1. The following Remark 4.2 is closely related to Mike’s pullback condition: if you want a map between models to be compatible with the models’ interpretations of formulas in the theory, then the restriction (resp. pullback along ) of your map to the interpretation of a formula in should land in the subobject (resp. should come from ).
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeMay 28th 2017
Thanks. I noticed that an entry “elementary embedding” was missing from model theory - contents and so I added it. In the course of this I rearranged slightly the list of keywords at the beginning, trying to put them more in logical order. Now it starts out like this:
…
-
- CommentRowNumber9.
- CommentAuthorJohn Baez
- CommentTimeNov 22nd 2020
- (edited Nov 22nd 2020)
I’m confused by this passage in elementary embedding:
More generally, when we consider structures in a category as in categorical logic, a morphism between structures in is an elementary embedding if for any formula , the following square is a pullback:
where denotes the object of interpreting the type , and denotes the corresponding subobject in interpreting the truth value of the formula .
One problem is that the types appear “out of the blue” - we start by saying “ between structures in is an elementary embedding if for any formula …”, and none of this mentions types . Can we add something to explain what they are, and what the are, and what the maps are? I’d do this myself if I could.
-
- CommentRowNumber10.
- CommentAuthorDavid_Corfield
- CommentTimeNov 23rd 2020
It seems that the are the types implicitly referred to earlier:
parameters (of appropriate types)
So this is typed first-order logic?
-
- CommentRowNumber11.
- CommentAuthornLab edit announcer
- CommentTimeNov 24th 2020
1 to 11 of 11