nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 17th 2009
expanded the Idea-section at Bousfield localization (by shamelessly following the introduction of Clark Barwick's nice article, referenced there)
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 17th 2009
added the Smith-Barwick existence theorem to Bousfield localization
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
expanded the "Properties" section at Bousfield localization with more and more detailed theorems
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeNov 18th 2009
If A and B are abelian and Q:A -> B an additive localization functor having fully faithful right adjoint. Is then the total left derived functor LQ:D(A) -> D(B) automatically a Bousefield localization (no additional assumptions) ? Where can one find the details ? -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 20th 2009
Zoran, I don't know. by
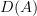 and
and 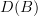 I suppose you mean the model categories of complexes insteadof the derived categories? Otherwise I am not sure what Bousfield localization should mean, for derived categories.
I suppose you mean the model categories of complexes insteadof the derived categories? Otherwise I am not sure what Bousfield localization should mean, for derived categories. -
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeNov 20th 2009
- (edited Nov 20th 2009)
At Existence of Bousfield localization I spelled out the proof (from Barwick's article) that every left proper combinatorial model category has all Bousfield localizaitons at sets of morphisms. Using Jeff Smith's recognition theorem for combinatorial model categories, this is comparatively easy.
But I seem to have one confusion about filtered colimits:
Question
Why is every
 -filtered colimit in a model category necessarily a homotopy colimit, for sufficiently large
-filtered colimit in a model category necessarily a homotopy colimit, for sufficiently large  ?
?I seem to have a worse confusion, which probably shows that I am suffering from an elementary misundersstanding of something:
at small object it says that that a
 -compact obect for regular
-compact obect for regular  is also compact for all
is also compact for all 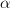 greater than
greater than  . But clearly also for all
. But clearly also for all 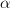 lower than
lower than  . So for all
. So for all 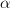 ? What's wrong here??
? What's wrong here?? -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 20th 2009
Added also Dugger's theorem saying that every combinatorial model category is a left Bousfield localization of the global projective model structure on simplicial presheaves on some small category.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeNov 20th 2009
> Otherwise I am not sure what Bousfield localization should mean, for derived categories.
I wrote long time ago the section in Bousfield localization about the triangulated case which is simpler in fact. -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeNov 20th 2009
Do you have a reference for that?
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeNov 20th 2009
- (edited Nov 20th 2009)
I suppose the Neeman's book on triangulated categories (which can be found free online) is the standard reference; I myself I think when writing the section used one of the papers of Neeman-Ranicki to check the facts. These things are often quoted in the literature on triangulated categories, specially those of algebraic geometry flavour (I would look in some articles of Keller, Rouqier, Balmer...). -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeNov 23rd 2009
- (edited Nov 23rd 2009)
Thanks, Zoran. Currently I will concentrate on the Bousfield localization of model categories. I hope to find time to look into localization of triangulated categorries later. I find it a bit confusing that this is supposed to be called Bousfield localization, too. All the literature that I have looked at so far (Hirschhorn, Lurie, Barwick) use "Bousfield localization" for localization of model categories and don't mention any other flavor. I am hoping the one on triangulated categories is the image under passing to homotopy categories of the full one applied to categories of complexes.
I am planning to type into the nLab entry a full detailed list of statements and proofs for Bousfield localizations of combinatorial model categories. I was thinking a bit whether to follow Hirschhorn, Lurie or Barwick on this, which are all similar but differ a bit in the approaches used in the proofs. Barwick's proof looks very slick, but so far I failed to follow one of his central lemmas:
he says that in a left proper model category all pushouts of cofibrations are homotopy pushouts. I do see the weaker statement that pushouts along cofibrations with cofibrant domain are homotopy pushouts. I have typed this now into Proper model category -- propeties. But presently I fail to follow Barwick's proof of the stronger statement on page 9 here.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
added section relation to presentable (oo,1)-categories -- mainly to serve as a reply for a Mathverflow question for the moment
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
rewrote the Idea section of Bousfield localization, trying to make it more succinct.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeNov 25th 2009
more details in the proof of the main theorem here, but am too tired now, will continue tomorrow
-
- CommentRowNumber15.
- CommentAuthorDmitri Pavlov
- CommentTimeMay 2nd 2020
-
- CommentRowNumber16.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 28th 2023
1 to 16 of 16