nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorAndrew Stacey
- CommentTimeNov 17th 2009
Created universal algebra in a monoidal category
In the lab book metaphor, this page is some jottings of stuff that I'm pretty sure must be out there (as it's a fairly obvious thing to do) but have no idea of what it's called (hedgehogs, perhaps?). So I'd be grateful if someone strong in the ways of Lawvere theories could stop by and help me out.
(Plus I had to make up the notation and terminology as I went along so that's all horrible)
Hopefully the big box at the top of the page makes this clear!
-
- CommentRowNumber2.
- CommentAuthorTodd_Trimble
- CommentTimeNov 17th 2009
Andrew, the monoidal version of a Lawvere theory is called a PRO (back-formation from PROP -- take away the P for permutations). I'll stop by later today on that page. -
- CommentRowNumber3.
- CommentAuthorAndrew Stacey
- CommentTimeNov 17th 2009
Of course! A "PRO", now why didn't I think of that?
Seriously, thanks! I look forward to reading what you write.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 17th 2009
<p><blockquopte></p> <p>A "PRO", now why didn't I think of that?</p> <p></blockquote></p> <p>Indeed. One of the good examples for bad terminology, I'd say. Unfortunately.</p> -
- CommentRowNumber5.
- CommentAuthorAndrew Stacey
- CommentTimeNov 18th 2009
Replied to Toby's question: In short, yes to the merge, but I don't feel that I have the expertise to do it.
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeNov 18th 2009
I added some commentary under 'Trade' and an answer to the question at the bottom. -
- CommentRowNumber7.
- CommentAuthorAndrew Stacey
- CommentTimeNov 18th 2009
Responded to the commentary with hopefully something a little clearer (be patient with me! Whilst I know quite well the little bit I'm trying to do, the general set-up is unfamiliar so I'll probably go on being unclear for a while). Forgot to say "thank you" for the answer so shall do so now: thank you.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeNov 18th 2009
My first acquaintance with that field systematically was
S. Lack, Composing PROPS, [Theory Appl. Categ.](http://www.tac.mta.ca/tac/volumes/13/9/13-09abs.html) 13 (2004), No. 9, 147--163. -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
somebody please add this reference to a relevant nLab entry
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
It's already at distributive law.
PS @ Zoran: Pick the ‘Markdown’ button below the comment field to make your link work as you intended.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
But it should probably be also in an entry on PRO(P)s
-
- CommentRowNumber12.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
OK, now it's in PROP.
-
- CommentRowNumber13.
- CommentAuthorAndrew Stacey
- CommentTimeNov 18th 2009
Reply to Todd at universal algebra in a monoidal category
-
- CommentRowNumber14.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
I'm also conversing there.
@ Urs: Todd added the reference there too!
-
- CommentRowNumber15.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
I think that the word monoidal in the definition of "monoidal T-object" is superfluous. In the case of PROs one uses often terminology a "representation of T" or a "T-module". -
- CommentRowNumber16.
- CommentAuthorAndrew Stacey
- CommentTimeNov 19th 2009
More clarification at universal algebra in a monoidal category.
Zoran, I think that was a hang-over from when I didn't know what a PRO was. Now that I know, that page should be merged with PRO and the terminology corrected.
(Incidentally, what's the convention: do we keep mentioning that we've replied over there? Or do we assume that everyone who's interested is keeping an eye on that page? I guess an edit brings it to the top of the general n-lab RSS feed. I'm happy with either convention, but I have a mild preference for keeping on mentioning it here as I'm hoping that Gavin Wraith will join in)
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
it can't hurt to mention all edits here
-
- CommentRowNumber18.
- CommentAuthorTodd_Trimble
- CommentTimeNov 19th 2009
This thread is probably a good excuse to build a page for the notion of measure coalgebra, which I'll get started on. -
- CommentRowNumber19.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
One thing which I always wondered is about lax and pseudo versions of representations of PROs and PROPs. For example, one could say I hope that a nonstrict monoidal category is nothing but a representation in pseudo sense of a PRO of monoids in Cat with cartesian monoidal structure. In a similar manner one can use certain PRO with ternary operations to define something similar to monoidal categories, with ternary products, which I call heapy categories, but I did not really study them enough (coherence theorem etc.). I wrote something about them in last section of a paper mentioned at quantum heap. -
- CommentRowNumber20.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
A nonstrict monoidal category is indeed a pseudo-algebra for the PRO of monoids in Cat. Actually, I would regard PROs as unnecessary complication, since operads or monads suffice, but they have the same algebras and pseudo algebras.
There is one issue, though: a nonstrict monoidal category is usually defined in a "biased" way (having only binary and nullary tensor products), while a pseudo-algebra for the PRO of monoids in Cat is an "unbiased" monoidal category, having one n-ary tensor product for every n. The two are equivalent (and often in practice we speak as if our monoidal categories were unbiased anyway), but the equivalence of the two basically requires all of Mac Lane's coherence theorem for (biased) monoidal categories.
-
- CommentRowNumber21.
- CommentAuthorDavid_Corfield
- CommentTimeNov 19th 2009
Could you explain, Todd (or anyone), why it's called a measure coalgebra. What does measure mean here? -
- CommentRowNumber22.
- CommentAuthorTodd_Trimble
- CommentTimeNov 19th 2009
- (edited Nov 20th 2009)
The only reference I have for this notion is a brief private conversation I had once with Martin Hyland; I don't recall if I asked or if he told me why. But I was hoping to construct a little story about it anyway, by calculating something like
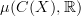 where
where 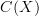 is the ring of continuous functions on a space
is the ring of continuous functions on a space  . I'll bet one can see some classical measures crop up there. In passing, I think I recall observing once that distributions supported at a point admit a coalgebra structure. All this stuff deserves to be recorded at the Lab.
. I'll bet one can see some classical measures crop up there. In passing, I think I recall observing once that distributions supported at a point admit a coalgebra structure. All this stuff deserves to be recorded at the Lab. -
- CommentRowNumber23.
- CommentAuthorTodd_Trimble
- CommentTimeNov 19th 2009
Incidentally, do the double dollar signs not work anymore? I can't get latex to appear correctly. -
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
Did you maybe accidentally switch the text filter (seen below the edit window)? At least for "Markdown" text filter it should work.
I didn't even know that we have text filters here, until I accidentally changed it by hitting some keys.
-
- CommentRowNumber25.
- CommentAuthorTodd_Trimble
- CommentTimeNov 20th 2009
Ah, that was it -- thanks.
-
- CommentRowNumber26.
- CommentAuthorAndrew Stacey
- CommentTimeNov 20th 2009
Hopefully now it's clear what I'm trying to do. Essentially, Toby and Todd's attempts to understand were correct and it was just my poor explanations getting in the way.
-
- CommentRowNumber27.
- CommentAuthorTodd_Trimble
- CommentTimeNov 20th 2009
Yes, I believe it is more or less clear Andrew, and it's got me thinking about some things coalgebraic which I mean to set down soon. There's probably a nice story to be told.
-
- CommentRowNumber28.
- CommentAuthorAndrew Stacey
- CommentTimeNov 20th 2009
Excellent! I look forward to reading it. If I'm allowed to make a request, can you put in references where you know them?
A lot of this stuff (or at least, the part relating to the bits I'm interested in) seems scattered across the literature with no particular thread to help find it. My coauthor and I would often argue something through only to find that some obscure paper from 50 years ago has the essential details, but we only found it almost by accident! Often, it would be some side remark that you made on the cafe!
Thanks!
-
- CommentRowNumber29.
- CommentAuthorTodd_Trimble
- CommentTimeNov 20th 2009
@David (and potentially Andrew): apparently what I am calling "measure coalgebra" is better know as "universal measuring coalgebra", and is discussed in chapter 7 of Sweedler's book Hopf Algebras. I don't have access to this book however.
I plan to write a little more about that construction later. If someone has access to that book, then I might want to compare notes at some point.
-
- CommentRowNumber30.
- CommentAuthorDavid_Corfield
- CommentTimeNov 21st 2009
On bimeasurings and On bimeasurings II talk about measurings and the universal measuring coalgebra. From the latter I see there's a 'dual Eckmann-Hilton theorem' about compatible co-structures being co-commutative. Never thought of that. -
- CommentRowNumber31.
- CommentAuthorzskoda
- CommentTimeNov 21st 2009
On the other hand it does not look complicated.
-
- CommentRowNumber32.
- CommentAuthorTodd_Trimble
- CommentTimeNov 21st 2009
- (edited Nov 21st 2009)
Continuation of discussion in query box over at universal algebra in a monoidal category, just putting down some things that Andrew no doubt observed already to himself. Reference to paper by Barr.
-
- CommentRowNumber33.
- CommentAuthorTodd_Trimble
- CommentTimeNov 23rd 2009
Answer to Andrew's question 1 at universal algebra in a monoidal category, in the negative.
-
- CommentRowNumber34.
- CommentAuthorAndrew Stacey
- CommentTimeDec 7th 2009
Returning to this, I now think that what I actually want is an operad but possibly without the symmetric group action (I need to check whether or not I truly have a symmetric monoidal structure). I hadn't realised the significance of the number of outputs: when the product is the cartesian product then, of course, a morphism into a product is a combination of morphisms into the single base object. I have a nice correspondence between the monoidal product in my category and the cartesian product on the underlying sets, but that works for morphisms out and I don't think it works for morphisms in. Therefore I need to ensure that I have only one output for my (generalised) operations.
Talk about going the long way round!
Incidentally, is there an operad version of a PRO? That is, without the symmetric group action?
-
- CommentRowNumber35.
- CommentAuthorAndrew Stacey
- CommentTimeDec 7th 2009
D'oh. Follow the links, Luke: multicategory claims that what I'm after is a Stasheff operad.
1 to 35 of 35