nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
added the general definition to cofibrantly generated model category
(that entry still deserves more attention, though...)
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 23rd 2009
added to cofibrantly generated model category the statement and proof of Kan's "recognition theorem" under Properties.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
removed from cofibrantly generated model category the extra section on presentable ones, which became superfluous after Mike (if I saw correctly) added the clause that generating cofibrations and acyclic cofibrations admit the small object aregument.
Instead, I moved now the statement that
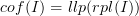 below the main definition and supplied the details of the proof
below the main definition and supplied the details of the proof -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeApr 15th 2012
Started at cofibrantly generated model category a section Presentation and generation with some statement. To be expanded.
-
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeJul 21st 2013
Does anyone have a reference for non-cofibrantly generation of pro-space (and more generally pro-model category) model structures? Boris Chorny makes reference to this in one of his papers, but I cannot find the comment in the referred paper (at least on the version I have of it).
It seems that pro-spaces have a fibrantly generated model structure on the other hand. Again does any one know good references for such (other than taking the dual of a cofib one)? These would seem to be important in some of the motivic contexts, but I quickly get out of my depth there. I am needing this for the profinite homotopy stuff that I am writing but will eventually put more on the Lab.
-
- CommentRowNumber6.
- CommentAuthorZhen Lin
- CommentTimeJul 21st 2013
Perhaps you’re thinking of Isaksen [2001], A model structure on the category of pro-simplicial sets? There it is remarked that the factorisations are not even functorial – so it’s neither fibrantly nor cofibrantly generated. (To be clear, what is proved (§ 19) is that it is not cofibrantly generated; but Isaksen says that factorisations are not functorial either.)
-
- CommentRowNumber7.
- CommentAuthorTim_Porter
- CommentTimeJul 21st 2013
- (edited Jul 21st 2013)
Thanks, Zhen Lin. I checked my preprint copy and found no section 19. I must have an earlier version. I will look for the newer version. (I have found the TAMS version on my hard disc, so fine, and again thanks.)
-
- CommentRowNumber8.
- CommentAuthorTim_Porter
- CommentTimeJul 22nd 2013
Actually, the proof of factorisation suffers from the inadequacy of language. Isaaksen shows that there is a factorisation but does not claim that it is functorial. in the process he says it is
non-functorial' rather than sayingfunctoriality is not claimed’ or similar. This looks a bit like an example of the red herring principle in disguise!These interactions between the set theory used for setting up pro-sSet and the small object argument intrigue me. Does anyone have any ‘wisdom’ to enlighten me? (Note it seems that pro-sSet may be fibrantly generated!)
-
- CommentRowNumber9.
- CommentAuthorDmitri Pavlov
- CommentTimeJun 24th 2022
Added:
The original reference is Chapter II of
- William G. Dwyer, Philip S. Hirschhorn, Daniel M. Kan, Model Categories and More General Abstract Homotopy Theory, PDF
In particular, the Kan recognition theorem is in §II.8 and the Kan transfer theorem is in §II.9. This manuscript draft later transformed in Homotopy Limit Functors on Model Categories and Homotopical Categories, losing the content on cofibrantly generated model categories in the process.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeAug 8th 2022
added hyperlink to Kan transfer theorem
1 to 10 of 10