Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: cofibrantly generated model category

Bottom of Page

1 to 10 of 10

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 19th 2009

    added the general definition to cofibrantly generated model category

    (that entry still deserves more attention, though...)

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeNov 23rd 2009

    added to cofibrantly generated model category the statement and proof of Kan's "recognition theorem" under Properties.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 24th 2009

    removed from cofibrantly generated model category the extra section on presentable ones, which became superfluous after Mike (if I saw correctly) added the clause that generating cofibrations and acyclic cofibrations admit the small object aregument.

    Instead, I moved now the statement that 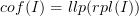cof(I) = llp(rpl(I)) below the main definition and supplied the details of the proof

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeApr 15th 2012

    Started at cofibrantly generated model category a section Presentation and generation with some statement. To be expanded.

    • CommentRowNumber5.
    • CommentAuthorTim_Porter
    • CommentTimeJul 21st 2013

    Does anyone have a reference for non-cofibrantly generation of pro-space (and more generally pro-model category) model structures? Boris Chorny makes reference to this in one of his papers, but I cannot find the comment in the referred paper (at least on the version I have of it).

    It seems that pro-spaces have a fibrantly generated model structure on the other hand. Again does any one know good references for such (other than taking the dual of a cofib one)? These would seem to be important in some of the motivic contexts, but I quickly get out of my depth there. I am needing this for the profinite homotopy stuff that I am writing but will eventually put more on the Lab.

    • CommentRowNumber6.
    • CommentAuthorZhen Lin
    • CommentTimeJul 21st 2013

    Perhaps you’re thinking of Isaksen [2001], A model structure on the category of pro-simplicial sets? There it is remarked that the factorisations are not even functorial – so it’s neither fibrantly nor cofibrantly generated. (To be clear, what is proved (§ 19) is that it is not cofibrantly generated; but Isaksen says that factorisations are not functorial either.)

    • CommentRowNumber7.
    • CommentAuthorTim_Porter
    • CommentTimeJul 21st 2013
    • (edited Jul 21st 2013)

    Thanks, Zhen Lin. I checked my preprint copy and found no section 19. I must have an earlier version. I will look for the newer version. (I have found the TAMS version on my hard disc, so fine, and again thanks.)

    • CommentRowNumber8.
    • CommentAuthorTim_Porter
    • CommentTimeJul 22nd 2013

    Actually, the proof of factorisation suffers from the inadequacy of language. Isaaksen shows that there is a factorisation but does not claim that it is functorial. in the process he says it is non-functorial' rather than sayingfunctoriality is not claimed’ or similar. This looks a bit like an example of the red herring principle in disguise!

    These interactions between the set theory used for setting up pro-sSet and the small object argument intrigue me. Does anyone have any ‘wisdom’ to enlighten me? (Note it seems that pro-sSet may be fibrantly generated!)

    • CommentRowNumber9.
    • CommentAuthorDmitri Pavlov
    • CommentTimeJun 24th 2022

    Added:

    The original reference is Chapter II of

    In particular, the Kan recognition theorem is in §II.8 and the Kan transfer theorem is in §II.9. This manuscript draft later transformed in Homotopy Limit Functors on Model Categories and Homotopical Categories, losing the content on cofibrantly generated model categories in the process.

    diff, v35, current

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeAug 8th 2022

    added hyperlink to Kan transfer theorem

    diff, v37, current

1 to 10 of 10

  1.