Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: cohomology

Bottom of Page

1 to 4 of 4

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 19th 2009

    wrote a fairly long Idea section at cohomology

    since the question keeps coming up and I noticed that the entry did a rather suboptimal job of describing the nice observation to be described here.

    • CommentRowNumber2.
    • CommentAuthorzskoda
    • CommentTimeNov 19th 2009
    I wrote few days ago at crossed product algebra some issues about "cocycled" case, where a generalization of a nonabelian group 2-cocycle to Hopf algebras appears ("factor system"). I do not really believe that such examples also come from standard model categories. Any idea how to generalize such cocycles for every n ?
    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 20th 2009

    I looked at crossed product algebra (also edited a bit, introducing some subsections). I don't see clearly yet.

    Could you remind me: do we have a simpler example of Hopf algebraic cocycles, where one could easier see what is going on? I would want to try to see if we can dualize all algebraic statements, at least morally, to get something that looks more like the familiar geometric examples, so that it would be easier to recognize a pattern.

    Currently I don't really see at all what is going on in the definition of that 2-cocycle 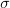\sigma that you discuss. Do you have any intuition for what is going on here?

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeNov 20th 2009
    • (edited Nov 20th 2009)
    But the generalization is mechanically almost trivial. I will now write it without checking (from memory) but the procedure is roughly the following. Take the usual group factor system G x G to B, say like in the case coming from 1->G->E->B->1 extension of groups (like in classical works of MacLane 1948 or so). Write down the linear extension of those to the group algebra (no dualization, this is linearization) i.e. to a bilinear map kG (x) kG to U=kB. Voila ! Now take this as a definition for every Hopf algebra H together with a measuring of H on U. The fact that we have measuring and not module is reflecting the generalization of the classical fact that we have a pseudofunctor.

    On the other hand, there are also special cases for Lie algebras and so on.

1 to 4 of 4

  1.