Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Questions related to the book Higher Topos Theory

Bottom of Page

1 to 7 of 7

  1.  
    • CommentRowNumber1.
    • CommentAuthorHarry Gindi
    • CommentTimeNov 21st 2009
    So as not to clutter up the whole board with questions about notation, I'm starting this thread so I can ask questions related to the topic.

    On page 24 of the book, while describing the simplicial nerve of a simplicial category where all of the morphism spaces are Kan complexes, I have two questions:

    Notation question: (\Delta^1)^{\{1,...,n-1\}} denotes what exactly? This notation is used nowhere else in the book, and nowhere else I've ever seen. In context:
    "Map_{C[\Delta^n]}(0,n) can be identified with the cube (\Delta^1)^{\{1,...,n-1\}} ..."

    Content question: In the paragraph where the above appears, it is enough to show that the vertical map is anodyne to prove the claim. Lurie then proceeds with a short proof by inspection, but I fail to see how this actually proves anything at all. how does that construction prove that the relevant map is anodyne.

    Thank you.
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeNov 23rd 2009

    You mean page 42 of the published book pdf, page 30 of the arXiv version (I like to look at the arXiv version, as that is fully hyper-cross linked, without that I find the book too large to read).

    I think the notation means literally the powering of the simplicial set 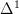\Delta^1 by the set 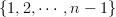\{1,2, \cdots, n-1\} , equivalently the internal hom by the latter, regarded as a discrete simplicial set. So this is equivalently just the cartesian product 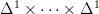\Delta^1 \times \cdots \times \Delta^1 of (n-1)-copies, hence a cube, in this sense.

    If we believe the analysis that the left vertical map in question is hence the incusion of the boundary of the cube minus one of its faces into the cube, then this is clearly an acyclic cofibration and hence anodyne.

    (Or so I think, let me know if I sound like I am mixed up.)

    • CommentRowNumber3.
    • CommentAuthorHarry Gindi
    • CommentTimeDec 9th 2009
    • (edited Dec 9th 2009)
    So, time for another HTT question! In the proof of proposition 2.1.2.1 on page 59 of the arXiv pdf, Lurie says that we can easily unravel the definitions to prove the proposition from 2.1.2.3 and 2.1.2.4, but I'm having trouble unraveling the definitions past the definition of an undercategory. The fact that the hom sets are required to have those restriction conditions is making it a huge pain in the neck to dualize it. It feels like I'm missing a small point here, since we know what kinds of maps we want to compose with (namely the projection and injection maps). I'm just stuck, and if someone can help unstick me, I'd be very grateful.

    Edit: I think I've figured it out, but I'm not absolutely positive. I think the trick here is to use the opposite yoneda embedding (C^op -> [C,Sets]) at the beginning of the proof to get it in the form used in 2.1.2.3. If this doesn't make sense, I guess just tell me?

  4. I looked for a book review of HTT but couldn’t find one. Is there any?

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeJun 29th 2012

    I thought there was a MathSciNet review. But maybe I am hallucinating. I cannot check myself right now.

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeJun 30th 2012

    There is a MathSciNet review: MR2522659

  7. Thanks. Unfortunately these are always absurdly complicated to access via my affiliated library…

1 to 7 of 7

  1.