Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration finite foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: directed colimit

Bottom of Page

1 to 13 of 13

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 26th 2009
    • (edited Nov 26th 2009)

    I added to directed colimit the \kappa -directed version, for some regular cardinal \kappa .

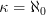    We should maybe also add to directed set the \kappa -directed version. What we currently descrribe there is just the \kappa = \aleph_0 -directed version.

    Accordingly then I also added to compact object the definition of the variant of \kappa -compact objects.

    At small object previously it mentioned " \kappa-filtered colimits". I now made that read " \kappa-directed colimits".

    I hope that's right. If not, do we need to beware of the differene?

    • CommentRowNumber2.
    • CommentAuthorTobyBartels
    • CommentTimeNov 26th 2009

    Well, there is a difference. Which is correct at small object I don't know. But many filtered colimits are not directed.

    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeNov 26th 2009
    • (edited Nov 26th 2009)

    ‘We should maybe also add to directed set the \kappa-directed version.’

    It's already there. But you could rearrange it, now that you need it to be more prominent.

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeNov 27th 2009

    Wait a second, isn't at least for the EXISTENCE of filtered colimits enough to have the existence of directed?

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeNov 27th 2009
    • (edited Nov 27th 2009)

    I'd think so, filtered is more general than directed.

    It seems I see authors use either filtered or directed when defining kappa-compact objects, though.

    • CommentRowNumber6.
    • CommentAuthorMike Shulman
    • CommentTimeNov 27th 2009
    According to 1.5 and 1.21 in Adamek & Rosicky, a category has k-directed colimits iff it has k-filtered ones, and a functor preserves k-directed colimits iff it preserves k-filtered ones.

    I prefer to state definitions using filtered colimits, myself, since many naturally occurring filtered colimits are not directed, including the essential example of the expression of an object of a locally presentable category as a canonical colimit of the k-small generators. I tend to view the fact that directed colimits suffice to obtain all filtered ones as a convenient coincidence, like the fact that all colimits can be constructed from coproducts and coequalizers.
    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeNov 27th 2009

    Thanks. I quickly copied that statement to here.

    • CommentRowNumber8.
    • CommentAuthorTobyBartels
    • CommentTimeNov 27th 2009
    • (edited Nov 27th 2009)

    I find the fact that all colimits can be constructed from coproducts and coequalizers more than a convenient coincidence. It's a recipe for constructing colimits (well, you need more details than just the theorem, but the usual proof has these). I think that I see how this works for filtered colimits too. Very nice.

    But I guess that you (Urs) mean that one would normally say that a category has all colimits rather than saying that a category has all coproducts and binary coequalisers. So similarly one should say that a category has all filtered colimits (or whatever one wants to say) rather than that it has all directed colimits.

    Probably somebody should write filtered colimit. OK, I started it, with material taken from filtered category; I added an Idea section to the latter to make up for its loss.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeNov 27th 2009

    Thanks for the filtered colimit page. i was thinking about creating that, but never found the energy. There are plenty of links on our pages that read "filtered colimit" but point to filtered category.

    • CommentRowNumber10.
    • CommentAuthorTobyBartels
    • CommentTimeNov 27th 2009

    I didn't realise that you were doing that! Possibly I have now changed them all.

    This is a perfect example of a case where redirects could have helped. If you'd added [[!redirects filtered colimit]] to filtered category, then all of these links would have worked as soon as I'd created the new page.

    • CommentRowNumber11.
    • CommentAuthorzskoda
    • CommentTimeNov 30th 2009
    Urs said "I'd think so, filtered is more general than directed."

    Urs I was saying the converse (so your confirmation sounded counterlogical), that even if more general filtered colimits, their existence is implied by the more special directed case, what Mike later confirmed with a reference. But now is there the same result about commuting and other similar statements ? (I mean if a functor commutes with directed colimits, does it commute with all filtered colimits) My understanding is that again yes, if we get the thing by combining the directed ones.
    • CommentRowNumber12.
    • CommentAuthorMike Shulman
    • CommentTimeNov 30th 2009

    To quote myself above, quoting A&R:

    a functor preserves k-directed colimits iff it preserves k-filtered ones.

    Category theorists say "preserve" where other people apparently say "commutes with".

    • CommentRowNumber13.
    • CommentAuthorzskoda
    • CommentTimeNov 30th 2009
    • (edited Nov 30th 2009)
    George (Janelidze) says (rightfully) that I do not know anything about category theory, so I must be among others anyway :) Somehow I missed the second part of your sentence in the first quotation (I do know that preserving is "commuting").

1 to 13 of 13

  1.