nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorzskoda
- CommentTimeNov 29th 2009
It seems to me that despite so lenghty discussions and entry related to the mapping space-hm adjunction, only the ideal situations are treated (convenient categories of spaces). For this reason, I have created a new entry exponential law for spaces containing the conditions usually used in the category of ALL topological spaces, as well as few remarks about the pointed spaces.
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeNov 29th 2009
Thanks, that's good to know.
One bit wasn't clear to me, so I asked a question.
Also, I changed
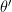 to
to 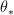 , which made sense to me; sorry if that's wrong.
, which made sense to me; sorry if that's wrong. -
- CommentRowNumber3.
- CommentAuthorTodd_Trimble
- CommentTimeNov 29th 2009
I added some further details on top of the article, since the exponentiability in
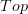 was not fully addressed. A useful reference has been added.
was not fully addressed. A useful reference has been added. -
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeNov 30th 2009
- (edited Nov 30th 2009)
It is OK to write theta with lower star, but this lower star is not induced by functoriality, but by a bit more explicit/careful consideration.
-
- CommentRowNumber5.
- CommentAuthorTodd_Trimble
- CommentTimeNov 30th 2009
I put a query over at locally compact space, although I think I already know the answer.
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeDec 4th 2009
There are many definitions of locally compact spaces in the literature, all equivalent for Hausdorff spaces, and it's difficult to untangle them. The page exponential law for spaces suggests that core-compactness is the deciding feature. Do we know enough to be Bourbaki and decide which is best?
-
- CommentRowNumber7.
- CommentAuthorTodd_Trimble
- CommentTimeDec 4th 2009
Yes, I believe so: the topology should be a continuous lattice, which means we should opt for the definition that says that compact neighborhoods of a point are a neighborhood basis, for every point. I may add that in in a bit.
-
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeMay 4th 2010
I did some reorganizing of exponential law for spaces, and added a reference to Claudio Pisani’s neat result characterizing exponentiable spaces in terms of ultrafilter convergence.
1 to 8 of 8