Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: fundamental groupoid

Bottom of Page

1 to 10 of 10

  1.  
    • CommentRowNumber1.
    • CommentAuthorGuest
    • CommentTimeDec 8th 2009
    Removed erroneous material (due to me) at fundamental groupoid regarding topological structure on fundamental groupoid, and reworded paragraph to indicate what actually is possible.

    David Roberts
    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeDec 9th 2009

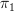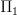    I did a bit of reorganization of this page, which had a bunch of different subjects all stuck together under "Remarks". It was also inconsistent about its use of \pi_1 and \Pi_1, so I tried to remedy that. I think the stuff about topologizing the fundamental groupoid is kind of confusing right now, but I don't know exactly what it's trying to say so I can't fix it.

    • CommentRowNumber3.
    • CommentAuthorGuest
    • CommentTimeDec 9th 2009
    Answered your question (I hope) at fundamental groupoid, but more needs to be done. There is probably some more reference to Ronnie Brown's work needed.

    David Roberts
    • CommentRowNumber4.
    • CommentAuthorGuest
    • CommentTimeDec 9th 2009
    A little more patch-up to do with topology on Pi_1.

    David Roberts
    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeDec 28th 2016

    I have added to the References-section at fundamental groupoid pointers to

    This observes that for good topological spaces and for Noetherian schemes the fundamental groupoid assignment Π 1(−)\Pi_1(-) is characterized as being 2-terminal among all co-stacks.

    • CommentRowNumber6.
    • CommentAuthorDmitri Pavlov
    • CommentTimeOct 25th 2019
    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeAug 14th 2022

    moving this ancient query box out of the entry:

    +– {: .query} Mike Shulman: Could you say something about what topology you have in mind here? Is the space of objects just XX with its original topology?

    David Roberts: The short answer is that it is propositions 4.17 and 4.18 in my thesis, but I will put it here soon.

    Regarding topology on the fundamental groupoid for a general space; it inherits a topology from the path space X IX^I, but there is also a topology (unless I’ve missed some subtlety) as given in 4.17 mentioned above, but the extant literature on the topological fundamental group uses the first one.

    Ronnie Brown: See the account in “Topology and Groupoids” referred to below. But there is also an account using path spaces in Proposition 6.2 of Mackenzie’s 1987 book “Lie groupoids and Lie algebroids in differential geometry”.
    =–

    diff, v36, current

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeJan 2nd 2023

    added missing pointers with more basic review and introduction:

    diff, v37, current

  9. Clarified definition

    Anonymous

    diff, v38, current

    • CommentRowNumber10.
    • CommentAuthorDmitri Pavlov
    • CommentTimeNov 17th 2023

    Added:

    A detailed treatment is available in

    diff, v42, current

1 to 10 of 10

  1.