nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorGuest
- CommentTimeDec 8th 2009
Removed erroneous material (due to me) at fundamental groupoid regarding topological structure on fundamental groupoid, and reworded paragraph to indicate what actually is possible.
David Roberts -
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeDec 9th 2009
I did a bit of reorganization of this page, which had a bunch of different subjects all stuck together under "Remarks". It was also inconsistent about its use of
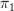 and
and 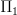 , so I tried to remedy that. I think the stuff about topologizing the fundamental groupoid is kind of confusing right now, but I don't know exactly what it's trying to say so I can't fix it.
, so I tried to remedy that. I think the stuff about topologizing the fundamental groupoid is kind of confusing right now, but I don't know exactly what it's trying to say so I can't fix it. -
- CommentRowNumber3.
- CommentAuthorGuest
- CommentTimeDec 9th 2009
Answered your question (I hope) at fundamental groupoid, but more needs to be done. There is probably some more reference to Ronnie Brown's work needed.
David Roberts -
- CommentRowNumber4.
- CommentAuthorGuest
- CommentTimeDec 9th 2009
A little more patch-up to do with topology on Pi_1.
David Roberts -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeDec 28th 2016
I have added to the References-section at fundamental groupoid pointers to
-
The fundamental groupoid as a terminal costack (arXiv:1406.4419)
The Étale Fundamental Groupoid as a Terminal Costack (arXiv:1412.5473)
This observes that for good topological spaces and for Noetherian schemes the fundamental groupoid assignment Π1(−) is characterized as being 2-terminal among all co-stacks.
-
- CommentRowNumber6.
- CommentAuthorDmitri Pavlov
- CommentTimeOct 25th 2019
Cross-linked with simplicial fundamental groupoid.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeAug 14th 2022
moving this ancient query box out of the entry:
+– {: .query} Mike Shulman: Could you say something about what topology you have in mind here? Is the space of objects just X with its original topology?
David Roberts: The short answer is that it is propositions 4.17 and 4.18 in my thesis, but I will put it here soon.
Regarding topology on the fundamental groupoid for a general space; it inherits a topology from the path space XI, but there is also a topology (unless I’ve missed some subtlety) as given in 4.17 mentioned above, but the extant literature on the topological fundamental group uses the first one.
Ronnie Brown: See the account in “Topology and Groupoids” referred to below. But there is also an account using path spaces in Proposition 6.2 of Mackenzie’s 1987 book “Lie groupoids and Lie algebroids in differential geometry”.
=–
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 2nd 2023
added missing pointers with more basic review and introduction:
Jesper Møller, The fundamental group and covering spaces (2011) [pdf]
Alberto Santini, Topological groupoids (2011) [pdf]
-
- CommentRowNumber9.
- CommentAuthornLab edit announcer
- CommentTimeJan 11th 2023
-
- CommentRowNumber10.
- CommentAuthorDmitri Pavlov
- CommentTimeNov 17th 2023
Added:
A detailed treatment is available in
- Nicolas Bourbaki, Topologie Algébrique, Chapitres 1 à 4, Springer, 2016. doi:10.1007/978-3-662-49361-8, ISBN 978-3-662-49361-8.
1 to 10 of 10