Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: A question on homotopy pullbacks

Bottom of Page

1 to 6 of 6

  1.  
  1. In the notations of homotopy pullback, is it true (eventually assuming that X,Y and Z are fibrant) that in case X --> Z is a weak equivalence then also P--> Y is a weak equivalence?
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeDec 12th 2009
    • (edited Dec 12th 2009)

    The homotopy pullback of a weak equivalence is a weak equivalence, yes.

    One way to see it is to compute the homotopy pullback in terms of the ordinary pullback over a fibrant replacement of the original diagram: the fibrant replacement diagram has fibrant objects and both morphisms are fibrations. If one of them was a weak equivalence before, it is now an acylic fibration. These are preserved under ordinary pullback, so the pullback morphism 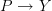P \to Y is then also an acyclic fibration and hence in particular a weak equivalence.

    More generally, homotopy pullbacks (at least in simplicially enriched model categories) model pullback in (oo,1)-catgeories. Their properties are structurally exactly those of ordinary pullbacks, just with everything working up to higher coherent homotopy. But the proof that the pullback in an (oo,1)-category of a morphism that is an equivalence is again an equivalence is entirely parallel to the proof that the ordinary pullback of an isomorphism is an isomorphism.

    • CommentRowNumber3.
    • CommentAuthordomenico_fiorenza
    • CommentTimeDec 12th 2009
    • (edited Dec 12th 2009)
    Thanks. that was precisely the argument I had in mind, but with the fibrant replacement I ended up with P --> R(Y) <-- Y, where R(Y) is the object in the fibrant replacement diagram over Y, with P -->R(Y) and R(Y) <-- Y both weak equivalences, and this told me that P and Y were weakly equivalent. But in this picture I had been unable to describe the direct arrow P --> Y one has in the universal homotopy cone description of the homotopy pullback. That's why I was wondering whether one needed the additional hypothesis for Y to be a fibrant object (now I clearly see this condition is suffcient to invert -up to homotopy- the acyclic cofibration Y --> R(Y) )
    • CommentRowNumber4.
    • CommentAuthorTim_Porter
    • CommentTimeAug 21st 2011

    There is a query at homotopy pullback.The questions answer is ‘Yes’ I think!

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeAug 21st 2011
    • (edited Aug 21st 2011)

    It seems you already fixed the entry somehow? Because currently I cannot understand what the question is about. (Or was about.)

    Should we not remove the query box then?

    • CommentRowNumber6.
    • CommentAuthorTim_Porter
    • CommentTimeAug 22nd 2011

    I fixed the diagram, but left the query so that ’Stephen’ would get the message about the forum. (I hope he has).

1 to 6 of 6

  1.