nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 17th 2009
Zoran created monadic descent
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeDec 18th 2009
started writing out at monadic descent the example section
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeDec 22nd 2009
- (edited Dec 22nd 2009)
behind the scenes Zoran and myself are having some discussion. In the course of this we have now
expanded the Details section at monadic descent -- this now for instance says explicitly that it is the algebras over the monads in question that encode the descent datum;
accordingly expanded the intro bit of the example monadic descent for codomain fibration -- this now states explicitly beforehand what the following discussion sets out to achieve: to show that algebras over the push-pull monad wrt the codomain fibration are ordinary "geometric" descent data
at Sweedler coring spelled out in the section In terms of comonadic descent explicitly how the comodules over a Sweedler coring are (co)algebras over the descent comonad, hence explicitly making the connection to (co)monadic descent.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeDec 22nd 2009
equivariant sheaf to support a discussion of the Galois condition versus (co)monadic descent which should appear soon...
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeDec 23rd 2009
I worked on Zoran's latest addition to monadic descent, which I now made the subsection called Monadic descent along principal bundles. Here is what I did:
created subsections
added an introductory paragraph with some guiding remarks
spelled out two of the double pullback diagrams that Zoran alluded to in the text
edited the formulas slightly: I gave the two monads names,
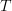 and
and 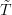 , and I renamed some
, and I renamed some 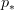 into
into 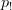 (hopefully correctly!)
(hopefully correctly!)
Apart from that I reacted to the query box in the section Monadic descent for bundles by correcting the typo, and I renamed the third subsection here and rephrased its introductory sentences, to make clear that what is being intended to be spelled out here is the data encoded in an algebra over the push-pull monad on a fiber of the codomain fibration.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeDec 23rd 2009
edited and expanded the entry bundle a little
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeDec 23rd 2009
added a bit to principal bundle. See the last three sections, which are new.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeDec 29th 2009
- (edited Dec 29th 2009)
Toby kindly corrected my doi link to Mohapeloa's article in a related article torsor by changing brackets to other version, but the link now does not work either, at least from my IE. My solution usually is to write the full html syntax rather than the wiki link when the addresses have special characters. What is the correct solution ?
Wait a second, now it works... (but still some advice could be useful, is there a table of changes I could do myself without waiting for Toby's help?).
Another technical question -- is there a way to see source code of others' code in nform discussions ? E.g. if somebody uses a LeTeX code, can I cut and paste in my answer when we discuss math ? It would be nice to be abel if it is not possible. It is bad that the cafe can't show the source code of posts and commentaries, unlike the all-mighty nlab.
-
- CommentRowNumber9.
- CommentAuthorTobyBartels
- CommentTimeDec 30th 2009
- (edited Dec 30th 2009)
If you use the
[text](URI)format for a link, which is otherwise very nice, you get problems if the URI has parentheses in it. (Actually only the right parenthesis causes problems.) These are fixed by changing(to%28and)to%29(which are more proper in URIs anyway, although modern browsers can handle the parentheses themselves).I had briefly messed up some of these DOI links, but I think that I corrected them all within a few minutes. So if it didn't work for a moment, that may be why.
(I don't know any way to see the source of anybody's comments except my own, but maybe Andrew will say something helpful about that.)
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeJan 12th 2010
- (edited Jan 12th 2010)
added to monadic descent reference to Hess's new article that appeared on the arXiv. Thanks to Zoran for pointing this out.
A quick look suggests that she is looking for a notion of (oo,1)-monads and their algebras. So I also added a pointer to (infinity,1)-monad
-
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeJan 12th 2010
When I was in 2004 at the IHES I lightly talked to Maxim Kontsevich and Sasha Rosenberg on need for descent theorems for monads in A-infinity category context, however it was not obvious what kind of conditions on homotopy limits etc. one needs for a monadicity theorems in that setup. Just on the day before I left they found a version of the monadicity theorem, in a train from Paris, but I heard just a short afternoon chat report on the outcome, and teh preprint which had to contain that is still as of today not released. A weker version in triangulated context can be found in Rosenberg's MPI preprint lectures on nc geometry and K-theory.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 12th 2010
Zoran and I decided to split off higher monadic descent.
I think Zoran is adding more references there right now.
-
- CommentRowNumber13.
- CommentAuthorFinnLawler
- CommentTimeJan 31st 2012
- (edited Jan 31st 2012)
Quick note: I found Bénabou and Roubaud’s article on the BnF website, so I added a link to monadic descent.
Edit: no, I didn’t; I added it to Benabou-Roubaud theorem.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeJan 31st 2012
no, I didn’t;
Okay, so I did it now.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMay 20th 2015
- (edited May 20th 2015)
At monadic descent, the previously existing “Details”-section discussed monadicity, not monadic descent as such. I have removed this and replaced it with some minimum discussion of monadic descent (in a new section Definition).
Then in a new section Examples – Descent for the codomain fibration I added the statement of the fact that for a locally Cartesian closed category with coequalizers, then the morphisms of effective descent for the codomain fibration are precisely the effective epis.
I also included pointers to Janelidze-Tholen 94, which is a good source on these matters.
Finally I gave Bénabou-Roubaud theorem a more genuine Idea-section.
1 to 15 of 15