nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 19th 2009
- (edited Dec 19th 2009)
I intend to considerbly expand the story at Atiyah Lie groupoid. But this afternoon I didn't get as far as I intended to, and now I have to quit and visit my parents. So this is to be continued. But so far I did this:
split off Atiyah Lie algebroid from Atiyah Lie groupoid
created a section Relation to differential nonabelian cohomology at Atiyah Lie groupoid that states a claim on how the Atiyah Lie groupoid fits into the story of nonabelian groupoid cohomology -- I wanted to type the proof, too, but ran out of time. Either someone takes it as an exercise and provides the proof, or I'll do so myself later today (or tomorrow)
created a stub for nonabelian groupoid cohomology. There exists a nice reference on "groupoid Schreier theory" that should go there, but I don't have time for that now
created inner automorphism 2-group to provide some background information needed in the statement of the above claim
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeDec 21st 2009
- (edited Dec 21st 2009)
in the section Relation to Differential Nonabelian Cohomology at Atiyah Lie groupoid details of the claim and the proof of how the Atyiah Lie groupoid
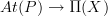 of a G-principal bundle
of a G-principal bundle 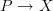 is a quotient of the homotopy fiber of the morphism
is a quotient of the homotopy fiber of the morphism 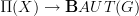 induced from a choice of connection on
induced from a choice of connection on  .
.I tried to present the argument in a supposedly nicely geometric fashion, with the homotopy pullback computed in terms of 2-groupoid incarnations of universal 2-bundles, but due to the restrictions of MathML diagrams it may look now a bit more awkward than it should, unfortunately.
I'll try to polish this further, eventually.
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeFeb 16th 2021
- (edited Feb 16th 2021)
Does anybody knows (it should be a long exercise, but maybe somebody sees and easy shortcut) how to express/formulate the Atiyah class in reasonably direct way in dual terms of algebra of smooth functions on Atiyah Lie groupoid/Ehresmann gauge groupoid or some holomorphic or algebraic geometric version instead of working from the start at tangent level of Lie algebroid ? I am interested because of noncommutative generalizations of Atiyah groupoid like Schauenburg bialgebroid, to see possible applications for nc connections on noncommutative principal bundles (of which several formalisms exist).
1 to 3 of 3