nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Classifying spaces and cohomology
Bottom of Page1 to 23 of 23
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 24th 2009
- (edited Dec 28th 2009)
In the Cech cohomology entry one finds that is naturally identified with (the colimit over all Cech covers of) , where is a Cech cover of . On the other hand it is well known that, for a nice topological space , is identified with . The topological realization of the nerve of is, if I'm not wrong here, the homotopy colimit of the groupoid as a topological groupoid, whereas is the colimit of .
With this in mind one ends up with an isomorphism
which suggests an equivalence
This should follow directly from some abstract argument, and reading all of the above backwords this would provide a construction of the classifying space. But I'm unable to see which abstract argument one should invoke here :( -
- CommentRowNumber2.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 26th 2009
- (edited Dec 28th 2009)
In the principal bundle entry one finds "Recall that for every group there is the the one-object groupoid . Under the Yoneda embedding this represents a prestack. Write for the corresponding stack obtained by stackification. This is our ". I totally agree that is obtained by stackification of the "trivial $G$-bundle" functor (which is a prestack), but I'm unable to see this as an issue of Yoneda embedding. This basically because I am only able to see the presheaf represented by as a presheaf on the same (infinity-)category is an object of. This seems to agree with what I've written a few lines later, where seems that both and should be objects in the same -topos . Yet, now seems to be the simplicial presheaf represented by , and sayng that this is already a simplical sheaf then seems to be a statement on . In any case, making both and objects of the same topos seems to require an explicitation of some missing (to me) ingredient. For instance, working with topological spaces, one could trade for the nerve of a Cech cover , in order to have two groupoids and consider , or see as the topological realization of its nerve, and look at . Both pictures seems to be valid -and actually to be equivalent-, but I'm unable to see them as without saying explicitly how and are seen in the same topos.
I apologize for such a confused post, with something clearer in my mind I could have tried editing the entry in the nLab instead.. :) -
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 26th 2009
I've now (finally..) read the cohomology entry, and everything became clear.. :) -
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 27th 2009
- (edited Dec 28th 2009)
Now that I've read cohomology the nonsense of the above posts has finally come into focus, so I'll try to restate it from the beginning, in a particular example to try to make it the clearer as possible.
Let be a (as nice as needed) topological space. I want to compute . The nPOV on cohomology tells me what I have to do is to look at both and as objects in a suitable -topos , and then consider the -groupoid .
To make this concrete I have two possibilities here. First, I can choose the prototypical -topos . Now is naturally an object in , and one can look at " in degree " as the strict -groupoid , and so as the topological space . That is I can recover from .
But I also have a second possibiliy. namely, I can look at as to an abelian sheaf, and choose the topos of -stacks on some site (topological spaces with open immersions? the open subsets of ?). This time and is shifted version are naturally simplicial sheaves, and one can look at as a simplicial sheaf via Yoneda embedding, and what one ends up with is that is recovered from or, if one wants to stress the Yoneda embedding, from .
The above tells in particular that the two -groupoids and have the same . So the natural question is: is there a homotopy equivalence ? -
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeDec 27th 2009
Well,
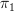 of each of them can be identified with
of each of them can be identified with 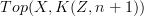 and
and 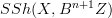 , respectively, and thereby with
, respectively, and thereby with 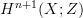 , and similarly for all higher homotopy groups. So all we need is a map inducing those isomorphisms. Perhaps there is an adjunction.
, and similarly for all higher homotopy groups. So all we need is a map inducing those isomorphisms. Perhaps there is an adjunction. -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 28th 2009
- (edited Dec 28th 2009)
I'm a bit confused here. It seems to me that the chain of isomorphisms ( stands for pointed topologicla spaces here) would rather imply that is isomorphic to . The reasoning above however is not affected by a +1 in place of -1, so I agree it says that not only but all the 's of the two infinity-groupoids involved are isomorphic.
As far as concerns finding a map inducing these isomorphisms, a strong enought version of Yoneda lemma (I've seen there's some discussion on this going on at Yoneda lemma for (infinity,1)-categories would imply that is equivalent to (I mean, consider both and as presheaves on ). So (Yoneda again) one is reduced to looking for an equivalence of simplicial preheaves between and . Since the latter is the presheaf associated to the topological realization of the first, all this hints to a topos version of the geometric realization/fundamental infinity-groupoid adjunction. -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeDec 28th 2009
I have come out of some Christmas vacation and have now worked on all my accumulated email and all the accumulated discussion here. I should reply to this here, too, but now I am running out of time.
Domenico, I understand that in the course of the above messages some of your questions found their answers already. Could you maybe summarize in a sentence or two what the remaining questions are?
(And include your LaTeX formulas in double dollar signs (inline), then they display pretty-printed here and are easier to read).
-
- CommentRowNumber8.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 28th 2009
- (edited Dec 28th 2009)
All of the above can probably be summarized in some suitably corrected version of following question: let be an abelian group and denote by the same symbol the corresponding constant simplicial presheaf over topological spaces (with open covers as covers); let be the topological realization of the nerve of . Look at as a presheaf on via Yoneda embedding. Are the two presheaves and equivalent?
(I edited the above posts with double dollars) -
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeDec 28th 2009
Oh, yeah, I added instead of subtracted, sorry. In too much of a hurry.
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeDec 28th 2009
Domenico, I think maybe you want to compare
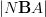 not to the constant simplicial presheaf
not to the constant simplicial presheaf  but to its delooping relative to the homotopy theory of simplicial (pre)sheaves?
but to its delooping relative to the homotopy theory of simplicial (pre)sheaves?I feel like something of this sort must be somewhere in HTT, since the introduction talks about identifying these two kinds of cohomology.
-
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 29th 2009
- (edited Dec 29th 2009)
Actually I do not exactly know what I want to compare, that's my main problem.. I'll try to look into HTT.
Basically these last days speculations on all came out from the idea of cohomology as it is stated at cohomology and, as a beatiful slogan, at nPOV. My point is that if we really want the nPOV on cohomology to be *the* point of view on cohomology (and I guess we want), we do not only need to identify each single cohomology theory with the of a space of infinity-morphisms in some (infinity,1)-topos, but also (and I find this to be the crucial point) exhibit all natural transformations of cohomology theories as morphisms of topoi.
I have two basic examples in mind. One is the subject of this forum entry: there are several possible natural topoi computations of ; how are they related? The other, I'm trying to write something about in my area, but I get more confuded each time I think to it: what are K-theory and the Chern character in the topos description of cohomology? -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeDec 29th 2009
- (edited Dec 29th 2009)
<div> <blockquote> Basically these last days speculations on all came out from the idea of <a href="https://ncatlab.org/nlab/show/cohomology">cohomology</a> as it is stated at cohomology and, as a beatiful slogan, at <a href="https://ncatlab.org/nlab/show/nPOV">nPOV</a>. </blockquote> <p>Thanks for that feedback. This made me include this slogan now in a standout box at <a href="https://ncatlab.org/nlab/show/cohomology">cohomology</a>.</p> <blockquote> also (and I find this to be the crucial point) exhibit all natural transformations of cohomology theories as morphisms of topoi. </blockquote> <p>Thanks, now I see what you are getting at.</p> <p>This deserves to be discussed, yes. As a first quick remark: what is ordinarily thought of as a morphism of cohomology theories happens inside a single (oo,1)-category, say between two functors represneted by two different spectra.</p> <p>Another thing I want to eventually discuss, which is relevant in this context, is this:</p> <p>for defining an (oo,1)-categorical hom-space of course all we need is an (oo,1)-category. So what is the point of requiring this to be an (oo,1)-topos?</p> <p>I think the answer is: if it is a topos, then we have the expected relation between cocycles and the objects they classify: every cocycles with coefficints in a pointed object classifies, by definition, its <a href="https://ncatlab.org/nlab/show/homotopy+fiber">homotopy fiber</a>. If the ambient (oo,1)-category is an (oo,1)-topos, then we have Giraud's axioms about effective groupoid objects, and using this we can conclude that this homotopy fiber behaves like a principal bundle. Parts of this is discussed at <a href="https://ncatlab.org/nlab/show/principal+infinity-bundle">principal infinity-bundle</a>.</p> <p>But I think it will make sense to also regard hom-spaces in non-toposes as cohomologies, of sorts, in particular in stable (oo,1)-categories. (Though the point of view keeps being expressed that every stable (oo,1)-category is somehow as good as an (oo,1)-topos.)</p> <blockquote> The other, I'm trying to write something about in my area, but I get more confuded each time I think to it: what are K-theory and the Chern character in the topos description of cohomology? </blockquote> <p>That's a very intersting point.</p> <p>The best abstract-nonsense description of what really happens with K-theory that I have seen is the one staated in the definition section at <a href="https://ncatlab.org/nlab/show/K-theory">K-theory</a>. This is taken from Lurie's "Stable (oo,1)-categories", equippedd with some additional remarks.</p> <p>Concerning Chern-character: this is something I am very much thinking about currently in the context of my work on <a href="https://ncatlab.org/schreiber/show/theory+of+differential+nonabelian+cohomology">theory of differential nonabelian cohomology (schreiber)</a>. I thinkl there is a good abstract-nonsense formulation using the <a href="http://ncatlab.org/schreiber/published/deRham+theorem+for+%E2%88%9E-Lie+groupoids">deRham theorem for oo-Lie groupoids</a>. I am currently busy with writing up more details on this. As soon as I am done replying to all sorts of forum discussions, I might actually have time to type this, then I get back to you!</p> </div> -
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 29th 2009
I'll look at your work on the Chern character, then :)
by the way, on second thought, the nPOV point of view on cohomology, 'thousands of definitions of notions of cohomology and its variants. From the nPOV, just a single concept: an infinity-categorical hom-space' immediately leads to the following rephrase: 'cohomology is the theory of representable functors in infinity-topoi', and then Yoneda allows a further rephrasement: 'cohomology is infinity-topos theory'. but I prefer the slogan the way you formulated it. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeDec 29th 2009
- (edited Dec 29th 2009)
<div> <blockquote> I'll look at your work on the Chern character, then :) </blockquote> <p>Okay. Maybe you can help me with one gap in my development that I still have:</p> <p>currently I am taking a detour through some oo-Lie theory for the full story:</p> <p>given an object <img src="/extensions/vLaTeX/cache/latex_e9fcd5f411ac341411f03f46e55c0ad7.png" title=" A " style="vertical-align: -20%;" class="tex" alt=" A "/> in a smooth (oo,1)-topos, I pass to its oo-Lie algebroid <img src="/extensions/vLaTeX/cache/latex_1b0319bca12e05b3240248dc1b06065b.png" title=" \mathfrak{a} " style="vertical-align: -20%;" class="tex" alt=" \mathfrak{a} "/>. For that I know how to nicely produce another oo-Lie algebroid <img src="/extensions/vLaTeX/cache/latex_335744e9417addee97dab8a30751e23c.png" title=" \mathfrak{a}_{ab} " style="vertical-align: -20%;" class="tex" alt=" \mathfrak{a}_{ab} "/>, which is something like the free abelianization of <img src="/extensions/vLaTeX/cache/latex_1b0319bca12e05b3240248dc1b06065b.png" title=" \mathfrak{a} " style="vertical-align: -20%;" class="tex" alt=" \mathfrak{a} "/>. For instance for the case that <img src="/extensions/vLaTeX/cache/latex_7907e1320a1ebed1f468d87d10815ead.png" title=" A = \mathbf{B}G " style="vertical-align: -20%;" class="tex" alt=" A = \mathbf{B}G "/> is a delooped Lie group, <img src="/extensions/vLaTeX/cache/latex_335744e9417addee97dab8a30751e23c.png" title=" \mathfrak{a}_{ab} " style="vertical-align: -20%;" class="tex" alt=" \mathfrak{a}_{ab} "/> is the thing such that its function algebra is the algebra of invariant polynomials on the Lie algebra of <img src="/extensions/vLaTeX/cache/latex_e9eec6c9fb23c40613a213b34d8c085f.png" title=" G " style="vertical-align: -20%;" class="tex" alt=" G "/>.</p> <p>Then I claim that there is a canonical morphism</p> <img src="/extensions/vLaTeX/cache/latex_2e4f0dd2228ab139e239aeae48d5ac9e.png" title=" H(X,A) \to H_{dR}(X, \mathfrak{a}_{ab})" style="vertical-align: -20%;" class="tex" alt=" H(X,A) \to H_{dR}(X, \mathfrak{a}_{ab})"/> <p>from cohomology with coefficients in <img src="/extensions/vLaTeX/cache/latex_e9fcd5f411ac341411f03f46e55c0ad7.png" title=" A " style="vertical-align: -20%;" class="tex" alt=" A "/> to deRham cohomology with coefficients in <img src="/extensions/vLaTeX/cache/latex_335744e9417addee97dab8a30751e23c.png" title=" \mathfrak{a}_{ab} " style="vertical-align: -20%;" class="tex" alt=" \mathfrak{a}_{ab} "/> (which is a collection of differential forms on X, one for each invariant polynomial) and that further postcomposed with the oo-deRham theorem that sends the deRham cohomology to real cohomology, this map is the general Chern character map for cohomology with coefficients in <img src="/extensions/vLaTeX/cache/latex_e9fcd5f411ac341411f03f46e55c0ad7.png" title=" A " style="vertical-align: -20%;" class="tex" alt=" A "/>.</p> <p>What I am lacking currently is a good way to make this statement without the detour throuh oo-Lie algebroids and deRham cohomology. Somehow I should be able to associate with <img src="/extensions/vLaTeX/cache/latex_e9fcd5f411ac341411f03f46e55c0ad7.png" title=" A " style="vertical-align: -20%;" class="tex" alt=" A "/> directly an oo-Lie groupoid that is something like the direct product of lots of Eilenber-MacLane spaces, one for each homotopy group of A, and then shifted up by one. I am not sure yet if I have found the best way to say this.</p> </div> -
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 29th 2009
I see your point, but I'm not fully confident a product of Eleinberg-Mac Lane spaces will work. Rather, I'd think to the Postnikov system for . I'll think to this.
The general picture, however seems quite clear: by Yoneda, a canonical morphism
must be induced, by composition, by an object in . so what we are interested in is the cohomology of . -
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeDec 29th 2009
- (edited Dec 29th 2009)
Right, exactly, we want an object consisting of lots of copies of
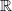 in various degrees, something like
in various degrees, something like 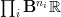 such that the entire real cohomology content of
such that the entire real cohomology content of 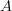 is encoded in a single morphism
is encoded in a single morphism 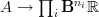 and then the Chern character map should be postcomposition with this morphism. I'd think.
and then the Chern character map should be postcomposition with this morphism. I'd think.Possibly this is looking for the rationalization of
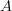 ...
... -
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 29th 2009
I wouldn't see things this way. Namely, I wouldn't look for a single morphism from to (some version of) encoding the whole cohomology . Rather, I would look at special (in some sense) objects of . For instance to go from K-theory of a (nice) topological space to its singular cohomology, one can use any polynomial (or even formal series) in the Chern classes, i.e. any element in the singular cohomology of to define a pullback morphism . But the Chern character is special since is a ring homomorphism. So I'd start with a (commutative?) ring object in and look for objects in inducing (?) ring homomorphisms by composition. I see in your consruction one begins with an arbitrary object , but maybe there's a groupoidification (and so maybe a ringification) hidden there in going from to (and then maybe integrating and taking some sort of ring of functions on the -groupoid one obtains. -
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeDec 29th 2009
I see your point. I am hoping for a description that does not need to assume that
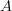 is a ring object, but maybe that'll be necessary.
is a ring object, but maybe that'll be necessary.I'll have to go offline very soon now. But I'll think about it.
-
- CommentRowNumber19.
- CommentAuthorTobyBartels
- CommentTimeDec 30th 2009
Reading your new slogan at cohomology, Urs, I'm reminded of Taylor & Wheeler, Spacetime Physics.
-
- CommentRowNumber20.
- CommentAuthordomenico_fiorenza
- CommentTimeDec 30th 2009
I finally managed to write something at Chern character in my nLab area. -
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeDec 30th 2009
- (edited Jan 4th 2010)
Thanks. I'll try to reply in a little while, after I have something else out of the way.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
- (edited Jan 4th 2010)
...
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
- (edited Jan 4th 2010)
Okay, now I'll come back to this discussion here.
I am beginning to think that the morphism that we are looking for above, that from some object
 in an (oo,1)-topos to some other object
in an (oo,1)-topos to some other object 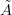 , such that postcomposition with this map maps
, such that postcomposition with this map maps  -valued cohomology to something like the corresponding "Chern character" is essentially the morphism
-valued cohomology to something like the corresponding "Chern character" is essentially the morphism 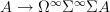
from
 to the free stabilization of its suspension.
to the free stabilization of its suspension.Or more precisely, as I indicated above, the construction is this:
let
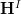 by the arrow category of the smooth ambient (oo,1)-topos. For
by the arrow category of the smooth ambient (oo,1)-topos. For ![[X \hookrightarrow \Pi(X)] [X \hookrightarrow \Pi(X)]](/extensions/vLaTeX/cache/latex_2340f38f94f75249699bd2a47715c835.png) the object in
the object in 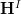 given by the inclusion of
given by the inclusion of  into its path oo-groupoid, and
into its path oo-groupoid, and ![[A \to *] [A \to *]](/extensions/vLaTeX/cache/latex_5aec67504caef8af7b754c193328c386.png) the map to the terminal object, we have that ordinary
the map to the terminal object, we have that ordinary  -cohomology of
-cohomology of  with coefficients in
with coefficients in 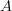 may be expressed in
may be expressed in 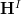 as
as ![\mathbf{H}(X,A) \simeq \mathbf{H}^I([X \to \Pi(X)], [A \to *]) \mathbf{H}(X,A) \simeq \mathbf{H}^I([X \to \Pi(X)], [A \to *])](/extensions/vLaTeX/cache/latex_56495bb63de2bca9352332afff954892.png) .
.Now let
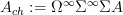 be the stabilization of the suspension object of
be the stabilization of the suspension object of 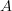 . The morphism
. The morphism 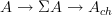 in
in 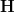 induces a morphism
induces a morphism ![[A \to *] \to [* \to A_{ch}] [A \to *] \to [* \to A_{ch}]](/extensions/vLaTeX/cache/latex_b732b5501f02df63e5c0912536bbd4f1.png) in
in 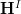 . So we get a morphism in cohomology
. So we get a morphism in cohomology![\mathbf{H}(X,A) \to \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}]) \mathbf{H}(X,A) \to \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}])](/extensions/vLaTeX/cache/latex_3a4667ca6aacc20de7417d81520bb779.png) .
.A cocycle in the thing on the right is a flat differential (i.e. on
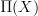 )
) 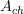 cocycle, whose underlying ordinary cocycle (i.e. on
cocycle, whose underlying ordinary cocycle (i.e. on  ) is trivial. This makes this a cocycle in the "real-ization" of
) is trivial. This makes this a cocycle in the "real-ization" of  : to see what I mean consider the archetypical case for instance that
: to see what I mean consider the archetypical case for instance that 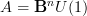 . Then an object in
. Then an object in ![\mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}]) \mathbf{H}^I([X \to \Pi(X)], [*\to A_{ch}])](/extensions/vLaTeX/cache/latex_fc38f70c4395725becba9ec2bd0a7235.png) is effectively a cocycle in
is effectively a cocycle in 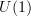 -Deligne cohomology whose 0-form part trivializes. But that's then the same as an
-Deligne cohomology whose 0-form part trivializes. But that's then the same as an 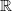 -Deligne cocycle (since the differential forms don't see the nontrivial topology of the coefficient object, only the 0-form part does, if we kill that, we are left with the real version).
-Deligne cocycle (since the differential forms don't see the nontrivial topology of the coefficient object, only the 0-form part does, if we kill that, we are left with the real version).So there is an object
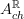 such that
such that![\mathbf{H}^I([X \to \Pi(X)], [* \to A_{ch}])\simeq\mathbf{H}(\Pi(X), A_{ch}^{\mathbb{R}}) \mathbf{H}^I([X \to \Pi(X)], [* \to A_{ch}])\simeq\mathbf{H}(\Pi(X), A_{ch}^{\mathbb{R}})](/extensions/vLaTeX/cache/latex_61df765f6c07edb12c2e650727721bc2.png)
I think. On the right we have a souped-up version of deRham cohomology. I think we may apply the deRham theorem for oo-groupoids to it to pass to a souped-up version of equivalent real cohomology. But since for the present purpose this just amounts to more notation, let me not do it. Then the punchline is that I am saying that the full generalization of the "Chern cheracter" that in ordinary differential cohomology would be suposed to map an Eilenberg-Steenrod cohomology theory
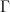 to ordinary real cohomology with coefficients in
to ordinary real cohomology with coefficients in 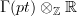 is the composite of the above maps
is the composite of the above maps
![H(X,A) \simeq H^I([X\to \Pi(X)], [A\to *]) \to H^I([X \to \Pi(X)], [* \to A_{ch}]) \simeq H(\Pi(X),A_{ch}^\mathbb{R}) \,. H(X,A) \simeq H^I([X\to \Pi(X)], [A\to *]) \to H^I([X \to \Pi(X)], [* \to A_{ch}]) \simeq H(\Pi(X),A_{ch}^\mathbb{R}) \,.](/extensions/vLaTeX/cache/latex_49eeae4666bd4dc9c3be18567cec3d72.png)
Here is something to check this statement. I am beginning to think the following is true, but I don't have a full proof yet:
for
 the oo-Lie groupoid of
the oo-Lie groupoid of  let
let 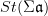 be the oo-Lie groupoid of the stabilization of
be the oo-Lie groupoid of the stabilization of 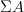 . Then I think the Chevalley-Eilenberg algebra (schreiber)
. Then I think the Chevalley-Eilenberg algebra (schreiber) 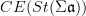 is the algebra of invariant polynomials on
is the algebra of invariant polynomials on  .
.I was looking for such a completely intrinsic oo-categorical definition of invariant polynomials for a while, and now I think this is it. But I still need to think about it.
Notice that, if right, this means for instance that for
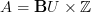 (the coefficient object for degree 0 K-theory) we have that
(the coefficient object for degree 0 K-theory) we have that 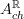 is the oo-Lie groupoid integrating the oo-Lie algebroid whose CE-algebra is that of invariant polynomials on
is the oo-Lie groupoid integrating the oo-Lie algebroid whose CE-algebra is that of invariant polynomials on  . But that's
. But that's 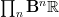 , hence the above generalized Chern-character for
, hence the above generalized Chern-character for 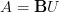 would take values in even graded real cohomology, which is the right answer.
would take values in even graded real cohomology, which is the right answer.Hm, Ill better stop here and dicsuss this in more detail on my web. I'll also have a look at the entry on your web now.
1 to 23 of 23