nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: Differential Graded (Noncommutative) Algebra of Whitney Forms
Bottom of Page1 to 2 of 2
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeJan 3rd 2010
- (edited Jan 3rd 2010)
I am pretty happy with what I just wrote at
Modified Wedge Product (ericforgy)
I proposed the idea years ago, but only now found a voice to express it in way that I think might resonate with others.
Basically, we have differential forms
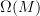 and cochains
and cochains 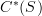 and maps:
and maps: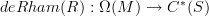
and
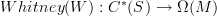
that satisfy
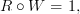 <br/>
<br/> <br/>
<br/>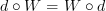 , and
, and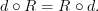
However, one thing that has always bugged me is that these maps do not behave well with products. The wedge product in
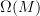 is graded commutative "on the nose" and the cup product in
is graded commutative "on the nose" and the cup product in 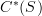 is not graded commutative "on the nose", but is graded commutative when you pass to cohomology.
is not graded commutative "on the nose", but is graded commutative when you pass to cohomology.The image of
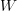 is called the space of "Whitney forms" and has been used for decades by engineers in computational physics due to the fact that Whitney forms provide a robust numerical approximation to smooth forms since the exterior derivative commutes with the Whitney map and we get exact conservation laws (cohomology is related to conserved quantities in physics).
is called the space of "Whitney forms" and has been used for decades by engineers in computational physics due to the fact that Whitney forms provide a robust numerical approximation to smooth forms since the exterior derivative commutes with the Whitney map and we get exact conservation laws (cohomology is related to conserved quantities in physics).One thing that always bugged me about Whitney forms is that they are not closed as an algebra under the ordinary wedge product, i.e. the wedge product of two Whitney forms is not a Whitney form. Motivated by this I proposed a new "modified wedge product" that turned Whitney forms into a graded differential algebra.
Now although in grade 0, Whitney forms commute, Whitney 0-forms and Whitney 1-forms do not commute except in the continuum limit where the modified wedge product converges to the ordinary wedge product and Whitney forms converge to smooth forms.
I think this might be a basis for examining the "cochain problem" John talked about in TWFs Week 288.
To the best of my knowledge, this is the first time a closed algebra of Whitney forms has been written down, although I would not be completely surprised if it is written down in some tome from 100 years ago (which I guess would be hard since it would predate Whitney).
Another nice thing about the differential graded noncommutative algebra of Whitney forms is that they are known to converge to smooth forms with sufficiently nice simplicial refinements (a kind of nice continuum limit) and you have true morphisms from the category of Whitney forms to the category of cochains (or however you want to say it). In other words, I believe the arrow theoretic properties of Whitney forms will be nicer than those of smooth forms.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
It should be true that
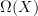 (the deRham dg-algebra) And
(the deRham dg-algebra) And 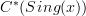 (the dg-algebra of cochains on simplicial sets)are, while not equivalent as dg-algebras, equivalent as E-infinity algebras.
(the dg-algebra of cochains on simplicial sets)are, while not equivalent as dg-algebras, equivalent as E-infinity algebras.Possibly what you describe gives a way to see that the functor
 exhibits that equivalence. But I haven't looked at the details.
exhibits that equivalence. But I haven't looked at the details.
1 to 2 of 2