nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
started oo-vector bundle on my personal web, following my latest remarks in the thread here on deformation theory.
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 5th 2010
- (edited Jan 5th 2010)
I do not understand your remark about free abelianization. The smallest abelian category containing the category of finite rank locally free sheaves of O-modules (aka algebraic vector bundles) is the category of coherent sheaves, rather than quasicoherent. The fibered category of quasicoherent sheaves appears rather as the category of qcoh sections of the fibered category of O-modules.
Another thing is that many functors are not defined at the level of coherent sheaves, thus to look at cohomology, injective resolutions etc. one needs to look coherent sheaves in a bigger category of qcoh sheaves.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
- (edited Jan 5th 2010)
Oh, so I got this worng. Thansk for pointing it out.
Hm, I think Lurie's theorem says that the oo-category
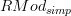 of modules over a simplicial ring
of modules over a simplicial ring 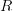 is equivalane to the stabilization of the overcategory
is equivalane to the stabilization of the overcategory 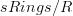 . This means, I think, that the oo-stack of oo-quasicoherent sheaves as used by Ben-Zvi et al is nothing but the assignment
. This means, I think, that the oo-stack of oo-quasicoherent sheaves as used by Ben-Zvi et al is nothing but the assignment 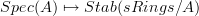 .
.This is the main statement that I am after.
But I guess I was too careless with associating this free stabilization with the abelianization that takes one from the ordinary Cat of vector bundles to quasicoherent sheaves.
So could you say this again: can one say in which sense the ordinary category of quasicoherent sheaves is a universal envelope of the category of vector bundles? Is there a good way?
-
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 5th 2010
I've just now started looking at infinity-vector bundles. me too disagrees on asking for abelianization. I'd rather ask nothing from the beginning, and would try to develop a simple and consistent categorical construction, if this will turn out to be abelianization in classical cases, the better; but otherwise it will be what it will be.
more in detail: in 'Ordinary algebraic vector bundles' I'm unable to see any abelianization or any other construction starting with "vector bundles"; rather it seems to me that quasicoherent sheaves are there from the very beginning, when rings and modules are considered.
a minor typo: Vect should start from Ring^op.
finally: does Sh(Ring^op) denotes sheaves with values in Set (and then a set is looked at as a trivial completely disconnected category) or with values in Cat? -
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeJan 5th 2010
I also think that it is other way around: finite rank locally free sheaves are just very special objects in Qcoh. It is like in affine situation finite rank free modules among all modules. But the fibered category of quasicoherent sheaves of O-modules may be obtained by a procedure from the fibered category of all O-modules. I would be also careful when generalizing from the affine case. For example it is an open problem wheather the category of qcoh sheaves on an arbitrary scheme has enough injectives.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeJan 6th 2010
- (edited Jan 6th 2010)
<div> <p>Thanks a lot for all the comments!</p> <blockquote> Vect should start from Ring^op. </blockquote> <p>I don't think it should. It should be a contrvariant functor on spaces, hence a covariant functor on rings.</p> <blockquote> finite rank locally free sheaves are just very special objects in Qcoh. </blockquote> <p>Sure, that's why I made a standout box saying that I use somewhat non-standard terminology. It's just that I find "oo-category of oo-quasi-coherent sheaves", denoted <img src="/extensions/vLaTeX/cache/latex_dc11e2fea52fdc295ffe86cf97326f0f.png" title=" QC(X)" style="vertical-align: -20%;" class="tex" alt=" QC(X)"/> not suggestive enough for such an important basic concept. I would like to write <img src="/extensions/vLaTeX/cache/latex_471faff06932f1061a4f9b6d0e05b11f.png" title="Vect(X)" style="vertical-align: -20%;" class="tex" alt="Vect(X)"/> instead. Maybe it's a bad idea to change notation this way, but I find "quasi-coherent" really a terrible term. It doesn't convey at all what it is about, and that it is about something very fundamental.</p> <p>So my entry is really to be read as labeled "oo-quasi-coherent sheaves", only that I idosyncratically say "oo-vector bundle" instead. Do you see what I mean? :-)</p> </div> -
- CommentRowNumber7.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 6th 2010
- (edited Jan 6th 2010)
**Vect should start from Ring^op.
I don't think it should. It should be a contrvariant functor on spaces, hence a covariant functor on rings.**
(I don't know how to quote...)
Absolutely. For some mysteriuous reason, yesterday I had taked the other direction in the bifibration, but it is clear the relevant one here is covariant in rings.
Let me try repair this by resuming the construction in 'Ordinary algebraic vector bundles':
One wonders: What is the categoty of quasicoherent sheaves on a scheme X?
Urs says: First you should tell me what a scheme is.
One: Something built by patching together affine schemes.
Urs: Ok, I know this: you are talking of the site Ring^{op}, and what you call X is a sheaf of Sets on Ring^op. What about the thing you call quasi-coherent sheaves? what is Qcoh(Spec(R))?
One: that's Mod_R, the category of R-modules
Urs: I see, that's what I call vector bundles on Spec(R)! (just kidding here ;-) ). So, we have two stacks over the site Ring^{op}. namely, the stack Vect, and the stack X (just look at a 0-category as to a category). by yoneda, Vect is nothing else that Hom(-, Vect), that is for any ring R, Vect(Spec(R)) is equivalent to Hom(Spec(R),Vect), where Spec(R) is seen as a stack over Ring^{op}. So I can see no beter definition for Vect(X) than saying that Vect(X) is by definition Hom(X,Vect).
One: ehm.. well.. I had in mind something without stacks.. once they had told me that a quasicoherent sheaf on X was a sheaf of O_X-modules such that I could find an open cover..
Urs: but that's exactly the same thing! Now, let's move to some more general site/bifibration.. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 6th 2010
<div> <blockquote> Urs: but that's exactly the same thing! </blockquote> <p>Yes, exactly. Now, I had thought there was a nice discussion of this in our entry on <a href="https://ncatlab.org/nlab/show/quasicoherent+sheaf">quasicoherent sheaf</a>, but checking now I see that there isn't. This needs to be included, now. Thanks for pushing me!</p> </div> -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 6th 2010
- (edited Jan 6th 2010)
Well, effectively the statement is in the subsection As sheaves on Aff/X. But the punchline should be highlighted much more...
-
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 6th 2010
now, something more serious.
in the classic 'ordinary vector bundles' setup one begins with Rings *and* Modules.
however, it is shown at deformation theory that there is a close relationship between Modules and [I,Rings], with R-modules realted to the overcategory Rings/R. This is the category of arrows pointing to R and so in the opposite category Ring^{op} one is considering the category of arrows stemming from R (or from Spec(R) if you prefer to say so), and it is extremely tempting to think of this as a sort of tangent space of Rings^{op} at the point R (this is very visual, arrows as vectors..).
so we learn that we should think to Modules over Rings as something related to a notion of tangent space to the site Rings^op.
I think this is very instructive, and I would paste this part from deformation theory into 'Ordinary algebraic vector bundles' to make clearer the connection with the tangent (infinity,1)-category of the site C in the general construction.
there's however still a point to be clarified: namely, which is the exact relationship between Modules and [I,Rings]? the general picture suggests this should be related to stabilization. making this clear would be a way of saying that (a version of) the category of Modules is entirely described in terms of the category of Rings, and it is precisely this description one mimics for an arbitrary site to define "infinity-vector bundles" -
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeJan 6th 2010
Renaming quasicoherent modules-sheaves-bundles into vector modules-sheaves'bundles is to my opinion bad. Coherence and quasicoherence are very intuitive and good terms. You see in smooth setup you can have bump functions, they appear when you go local, they are LOCAL surprises, not predicted from nearby fibers. On the other hand, coherence and quasicoherence have an essential ingredient that locally the localization is a procedure, not a passage to unknown completion with unknown new bumps. It is predictable result of a functor, which is the localization functor. All fibers over pointswork together in a coherent fashion, no democratic jumps around. Coherent dictature is the law!
Moreover, the maps between the fibers of the corresponding fibered category (here fiber is in a different sense than above) are isomorphisms, which could be considered as coherences also in the sense of the category theory. In fact, if we take a flat topology and look at the cover corresponding to the principal bundle over the base space, then the equivariant descent gives exactly the cocycle for the equivariance. Both are special cases of the same phenomenon of strictification of a fibered category.
I do not know why do you insist on a stabilization at the place where you discuss quasicoherence ? I mean abelianess is obtained before, at the level of O-modules. So you first have to get somehow by abstract nonsense (from your codomain fibration) the analogue of a category of O-modules. The second step is just the strictification to get from the fibered category of O-modules the fib category of qcoh modules. I can suspect something like abelianization or stabilization in the first step. The second is purely of quasicoherator nature (the functor which is outlines in Orlov's article by the way and before at places like EGA). I keep telling you this for last two years but it never develops into conversation, as you forget that there is first step and want to make both steps in one, and then I can not help you as I do not see them as one.
-
- CommentRowNumber12.
- CommentAuthorzskoda
- CommentTimeJan 6th 2010
An important thing to have in mind is that the isomorphism with the localization is true only along affine morphisms. In the treatment of affine schemes this difference is NOT seen as EVERY morphisms among affine schemes is affine (this is a fundamental property of affiness in any known setup), and affine schemes are just affine morphisms over Spec(Z), hence the conclusion. On the other hand, if you look at nonaffine schemes, then you have to look at which morphisms are affine to have the localization property.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
<p>Thanks again for all the comments. I went offline yesterday before I could reply to them.</p> <blockquote> I keep telling you this for last two years but it never develops into conversation, as you forget that there is first step and want to make both steps in one, and then I can not help you as I do not see them as one. </blockquote> <p>My apologies, Zoran, for being dense. I suppose I never understood what you were telling me.</p> <p>So let's sort this out in detail for plain QC sheaves first, before we continue talking about the oo-categorification further.</p> <p>I just made an attempt to add most of what I understand about QC sheaves to the entry <a href="https://ncatlab.org/nlab/show/quasicoherent+sheaf">quasicoherent sheaf</a>. Please see the announcement of the additions I made at <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=608&page=1#Item_1">quasicoherent sheaf (forum)</a>. Let me know what you think.</p> <p>Also Domenico, please have a look at the entry on QC sheaves now. It tries to make very explicit the way QC sheaves may be thought of from the <a href="https://ncatlab.org/nlab/show/nPOV">nPOV</a> as simply homs into the the stack of modules.</p> -
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
I will change the notation. I mean calling f* is fit to inverse image functor, not the map of rings. Map in the category of rings is just opposite to the map in the category of spectra. So I would either call f map of rings and Spec f map of spaces, or call f map of rings and f circ or f op the map of spectra.
-
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 7th 2010
I like the additions to quasicoherent sheaf very much. There are a few minor edits I'd do, as I'm able to find time for. For now, just let me say that I think in the Proposition at the beginning of As homs into the stack of modules there should be . the same typo seems to occur at times (but not systematically) also in the text below.
I'll also try to think to how to recover the classical case from the tangent (infinity,1)-category approach. -
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
Thanks, Zoran and Domenico, for fixing things!
-
- CommentRowNumber17.
- CommentAuthorzskoda
- CommentTimeJan 7th 2010
The strictification indirect way: take any category over a category. The category opposite to the category of it sections is the category of modules in it. Take any section and from it make a Grothendieck construction. Then take a section of the latter, what you obtain is a quasicoherent section. Quasicoherent modules are objects of the opposite category. They can be also expressed via cartesian sections from a trivial fibration.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
this morning I have worked on the entry and basically rewritten it, taking into account all the discussion we had, and also polishing this and that. I'd be very grateful if you could have another look
There are various immedie things to be done from here on. I indicate one in the new section on Associated oo-vector bundles.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
I have forwarded this discussion to the blog, here
-
- CommentRowNumber20.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
- (edited Jan 9th 2010)
I like infinity-vector+bundle#Associated a lot. instead of working with a representation at once, I'd rather write that in terms of composition: . This is particularly nice when $A=BG$ since it is the infinity-categorical version of
on the other hand I'm still unsure of how recover the classical theory (do we want to recover it) from the infinity-stable one. according to Lurie, in infinity-stable categories, looking at commutative rings as to simplicial commutative rings, what one ends up with over a ring R (more precisely R has to be a -algebra)
is not the category of R-modules but something stable which knows about the derived category of R-modules.
so, in going from an affine scheme to an arbitrary scheme $X$, it's likely that the tangent category approach does not really see but rather its stabilization or, maybe better, the stabilization of the category of complexes of quasicoherent sheaves on X.
here one can come back to one of the original issues between urs and zoran: what is Qcoh(X) to Vect(X)? we know that it is not abelianization, since Coh(X) is enough. but it may happen that Vect(X), Coh(X) and Qcoh(X) are stably equivalent, and so from a stable point of view there would be no difference between them. -
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
<div> <p>right, associating vector bundles is just composition of cocycles, which is just composition of morphisms in the oo-topos, yes.</p> <p>Concerning the other aspect you mention: it is true that with the tangent oo-category approach we don't get <em>just</em> the classical theory. But we get something into which the classical theory embeds.</p> <p>When we do this over <img src="/extensions/vLaTeX/cache/latex_34d0a67079d60aa8f0cd6ea8ad81abfa.png" title=" C = SRing^{op} " style="vertical-align: -20%;" class="tex" alt=" C = SRing^{op} "/> then, as the example 8.6 in "Stable oo-Categories" shows, <img src="/extensions/vLaTeX/cache/latex_03cf21e0dd38b8f3d0170d22802c53f4.png" title=" \infty Mod(R) " style="vertical-align: -20%;" class="tex" alt=" \infty Mod(R) "/> over an ordinary ring <img src="/extensions/vLaTeX/cache/latex_07473a8bf5ab2af6f9d299667342c3db.png" title=" R" style="vertical-align: -20%;" class="tex" alt=" R"/> is the oo-category whose homotopy category is the derived category of <img src="/extensions/vLaTeX/cache/latex_07473a8bf5ab2af6f9d299667342c3db.png" title=" R" style="vertical-align: -20%;" class="tex" alt=" R"/> -modules, yes. But ordinary modules still sit inside there.</p> <blockquote> here one can come back to one of the original issues between urs and zoran: what is Qcoh(X) to Vect(X)? we know that it is not abelianization, since Coh(X) is enough. </blockquote> <p>right, we need to say this precisely, eventually.</p> </div> -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
do coherent sheaves (not quasi-) form a bifibration? I.e. are they closed under push and pull?
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
they're not, right? already due to the finiteness condition.
-
- CommentRowNumber24.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
right. even with reasonable assumptions on the schemes and the morphisms one considers, is not coherent, but only quasi-coherent, in general (here obviously denotes a coherent sheaf).
as far as concerns Mod inside oo-Mod: are we sure of this? I've the doubt we may be unable to distinguish between two stably equivalent modules. but that's my unexperience in the field; I'll try to think more on this. -
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
<div> <p>Okay. Do we know if <img src="/extensions/vLaTeX/cache/latex_bab8fa3b10abe063ced5002f58a8b2a4.png" title=" QCOh(X)" style="vertical-align: -20%;" class="tex" alt=" QCOh(X)"/> is <em>exactly</em> what we get when we start with coherent sheaves and then complete under push-forward?</p> <p>(I have to say I'd be interested, but I don't really care so much. :-) The general nonsense def of QCoh(X) is so good, that I don't see a pressing need to find another universal characterization.)</p> <blockquote> I've the doubt we may be unable to distinguish between two stably equivalent modules. but that's my unexperience in the field; I'll try to think more on this. </blockquote> <p>Right, yes. I am not sure. Here, too, I don't really care too much. we know the right picture. What we are asking here is to which extent the wrong picture is preserved by the right picture. :-) Would be good to nail it down, but I am not losing sleep over this.</p> </div> -
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
I could not agree more :-) -
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeJan 9th 2010
- (edited Jan 9th 2010)
started a subsection on flat oo-vector bundles and D-modules
-
- CommentRowNumber28.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 9th 2010
I've now read David Ben-Zvi post on the blog. it clarified me a lot of the classical construction. as David says, the category of R-modules is the linearization of the overcategory Rings/R. here linearization means look inside Ring/R only at arrows which are infinitesimally close to the identity of R, and this can be conveniently formalized in terms of square-zero extensions of R. again, thinking in the opposite category Ring^{op}, we are considering "infinitesimal arrows stemming out fom Spec(R)", and this can conveniently be thought as the tangent category to Ring^{op} at Spec(R).
so we can talk of tangent category each time we have a notion of "infinitesimally close objects". however, we know from classical differential geometry that there is another approach to tangent spaces which needs not a notion of infinitesimally close points (even if this naive idea is motivating the construction and actually somehow hidden into it). namely, to construct one considers all (smoth) paths stemming from , i.e. the whole overcategory , and then quotients by a suitable equivalence relation. and, as usual, instead of quotienting we can add an isomorphisms between paths we want to identify. here I stop, cause I don't know exactly how to go on, but now I feel the abstract nonsense construction of as stabilization of overcategories more natural than a few days ago. -
- CommentRowNumber29.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 9th 2010
infinitesimal singular simplicial complex should have something to do with what I was trying to say above -
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
- (edited Jan 10th 2010)
There is a wording ordinary quasicoherent sheaves in the entry. As if D-modules were not ordinary quasicoherent sheaves, Full name is quasicoherent sheaves of O-modules in the first case and in the secondc case are the quasicoherent sheaves of D-modules. They are both quasicoherent sheaves in most ordinary sense, the difference is just weather of O-modules or of D-modules. The fact that by abuse of language geometers do not say qcoh sheaves of D-modules but only D-modules and not quasicoherent sheaves of O-modules but only qcoh sheaves or only qcoh modules is a different thing,
One should see if the qcoh 2-sheaves in the sense recently introduced by Toen in the arxiv preprint fits in this framework.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
by "ordinary" I mean "1-categorical" as opposed to the oo-version. I have now tried to clarify this.
By the way, what's a good reference that we could cite at D-module for the equivalence of D-modules with qcoh sheaves on the deRham space?
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
- (edited Jan 11th 2010)
I don't know, this is another point of view, equating D-modules with qcoh O-modules for another space, which I was not talking about. I put the reference of Beilinson-Bernstein on proof of Jantzen conjecture which is the main classical reference on D-affinity and algebraic D-geometry. I added some nlab links to D-module and the elementary textbook from Coutinho. I should say that I like your treatment of the interpretation via de Rham space.
-
- CommentRowNumber33.
- CommentAuthorzskoda
- CommentTimeAug 18th 2010
For usual vector bundles, I put some pain into producing a reference section in vector bundle with main monographs having lots of material on basic of the vector bundles.
-
- CommentRowNumber34.
- CommentAuthorzskoda
- CommentTimeAug 18th 2010
- (edited Aug 18th 2010)
Wait a second there is a strange section titled “Virtual vector bundles” in vector bundle – but instead of virtual vector bundles (like in Karoubi’s book: allowing vector bundles of different dimension/rank on different connected components of the base and also allowing negatives of vector bundles), there is a discussion on gradings which is related but not exactly what I recall from Karoubi (the pairs mean Grothendieck construction so one has negatives, but not the case of only locally constant rank) and there is also strange remark about “vectorial vector bundles” (??) there which I can not relate to virtual v.b.
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeAug 18th 2010
the notion of vectorial bundle is used by Gomi to model twisted K-theory using geometric objects. Have a look at the entry. These cocycles are not exactly the same as those of Karoubi, but their equivalence classes do model the same K-theory.
-
- CommentRowNumber36.
- CommentAuthorzskoda
- CommentTimeAug 18th 2010
Oh I remember looking at the paper, but not the expression. I should have followed the link.
1 to 36 of 36