Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: weighted join of quasi-categories

Bottom of Page

1 to 12 of 12

  1.  
  1. in order to discuss weighted limits in my revision of limits, I introduced a stubby notion of weighted join of quasi-categories. The construction and the subsequent notion of weighted limit seem quite natural, but everithing now seems too simple, so I fear to have completely misunderstood the notion of weighted limit.. :(

    could anybody give a look?
    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeJan 5th 2010

    Regarding limits, can I suggest that the nlab page on limits should not start out talking about quasicategories? (-: I'm not clear exactly what your plan is, but the page you have called limits (domenicofiorenza) doesn't seem appropriate for an nlab page called "limit" instead of, say, "limit in a quasicategory". Perhaps I have misunderstood what you're doing.

  3. you did not misunderstood: there has been some speculation between urs and me in the thread "objects and tools to compute them" on the oppurtunity of organizing nLab entries according to the pattern idea and motivation/infinity-categorical definition/unwrapping of the definition and specialization to categories/examples/how to compute.

    since abstract speculation on issues like this leads nowhere we agreed to give a try and rewrite a classic such as limit, to see how it came out. not to affect such a fundamental entry as limit the revision attemp is developed in my private area. as it will be completed it will be possible to discuss what to do with it: use it to replace "limit" in the nLab? merge it into "limit in a quasicategory" in the nLab? leave it as a memento of how an nLab page should *not* look? :-)

    I've no preferences, my attitude in developing limit is to consider it an exercise in style. but maybe something good can come out of it anyway. for instance, the approach to weighted limits via weighted joins, if I did not completely misunderstood the definition of weighted limit, may happen not to be so bad.
    • CommentRowNumber4.
    • CommentAuthorMike Shulman
    • CommentTimeJan 6th 2010

    I made a couple comments.

  5. Thanks. I see calling the category was a really bad choice. Now I've edited the page.
  6. @Mike: cograph of a profunctor, as you suggested, seems to perfecty do what I had in mind, thanks! I also added a short comment to try to explain what I meant by changing the notation.
  7. Mike, I'm glad in the end we managed to understand each other :-)

    As I'll be able to find time for, I'll rewrite everithing in weighted join in terms of cographs as you suggest.

    Just a final question: is not what I call a weighted initial object for D the weighted limit of id:D-->D? what am I missing?
    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeJan 8th 2010

    i don't have the energy to look into this right now, but am interested. If Mike finds a second I am sure you two will find a good notion of weighted (oo,1)-limit.

    • CommentRowNumber9.
    • CommentAuthorMike Shulman
    • CommentTimeJan 8th 2010
    • (edited Jan 8th 2010)

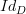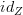    A W-weighted limit of Id_D would be an object Z such that hom_D(Y,Z) \cong [D,Set](W,hom_D(Y,-)) for all Y. In particular, looking at id_Z on the left-hand side would give you a canonical set of 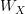W_X maps from Z to X for all X, i.e. a map 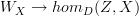W_X \to hom_D(Z,X), but I don't see any reason for that map to be a bijection.

    • CommentRowNumber10.
    • CommentAuthordomenico_fiorenza
    • CommentTimeJan 8th 2010
    • (edited Jan 8th 2010)
    I see, and neither I can see a reason for to be a bijection at the moment. what confuses me is that for the constant weight , this is actually a bijection, and a limit of turns out to be an initial object for . yet, the construction above, specialized to , apparently only provides a canonical map , thus only seems only to say that for every there is a certain distinguished map . but looking at things more in detail one finds that is the unique map from to . I'll have to think more on this.
    • CommentRowNumber11.
    • CommentAuthordomenico_fiorenza
    • CommentTimeJan 13th 2010
    • (edited Jan 13th 2010)
    Mike, I've finally found some time to think again to the definition of weighted limit, and now I totally agree with your objection, thanks.

    Summing up, things should go as follows. Let be a functor and let be a weight. If denotes the terminal category, then and can be seen as a profunctor from to . The cograph of this profunctor is the "weighted join" . The weighted limit of is, if it exists, a terminal object in the category of functors extending . If a weighted limit in this sense exists, then the object of has the universal property of the weighted limit of the "object with universal property" definition of weighted limit. And vice versa, given an object with the universal property, one can canonically extend to by setting . Hence the two notions are equivalent, and one can use the "terminal functor" definition to generalize the notion of weighted limit to quasicategories. What do you think?
    • CommentRowNumber12.
    • CommentAuthorMike Shulman
    • CommentTimeJan 14th 2010

    Yes, that seems right to me.

1 to 12 of 12

  1.